© 2006  Rasmus ehf  og Jóhann Ísak Pétursson

Þáttun liðastærða

Hvernig er hægt að reikna eftirfarandi margföldun til baka

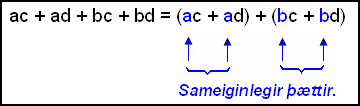
(a + b)(c + d) = ac + ad + bc + bd

Óbrigðul aðferð gengur út á það að þú skiptir stæðunni upp í tvo sviga þannig að hvor sviginn hafi tvo sameiginlega þætti sem taka má út fyrir sviga. Eftir standa þá tveir eins svigar

= (c + d)(a + b)

Þetta er lykilatriði að búa  til tvo eins sviga. Þeir verða síðan sameiginlegur þáttur sem má taka út fyrir alla stæðuna.

Ef þér finnst þetta torskilið prófaðu þá að kalla svigana S og setja  síðan S-ið inn í staðinn fyrir þá báða. Dæmið verður þá svona:

ac + ad + bc + bd = (ac + ad) + (bc + bd)

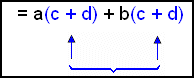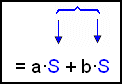Köllum svigann S og

 setjum S inn í hans stað í dæminu

= S(a + b)= (c + d)(a + b)

Tökum S út fyrir sviga.

Athugaðu að það skiptir ekki máli hvaða tveir eins svigar eru búnir til.

Dæmið mætti einnig reikna á eftirfarandi hátt.

ac + ad + bc + bd

= (ac + bc) + (ad + bd)

= c(a + b)+ d(a + b)

= (c(a + b) + d(a + b))

= (a + b)(c + d)

Þáttum  x² + x + ax + a.

 x² + x + ax + a

= x(x + 1) + a(x + 1)

= (x + 1)(x + a)

Þáttum  x³ − 4x² − x + 4.

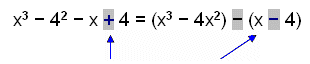Athugaðu að þetta merki breytist þegar það lokast inni í sviga sem er með mínus fyrir framan. Ef sviginn er felldur þá breytist merkið aftur enda var ekki meiningin að breyta dæminu.

 = x²(x − 4) − (x − 4)

= (x − 4)(x² − 1)    

Hér notum við samokaregluna

= (x − 4)(x + 1)(x − 1)

Þáttum  6x² + 13x + 6.

6x² + 13x + 6 = 6x² + 4x + 9x + 6

Hér kljúfum við 13x upp í 4x og 9x, en það þarf talsverða útsjónarsemi til þess að koma auga á þennan möguleika.

= (6x² + 4x) + (9x + 6) 

= (2x(3x + 2) + 3(3x + 2))

= (3x + 2)(2x + 3)