© 2007  Rasmus ehf    og Jóhann Ísak

Hornaföll

Kynning 4   Hornafallajöfnur og ójöfnur

Sýnidæmi 1

Leysum jöfnuna 2∙cos 3v° = 1 á bilinu .

   cos 3v° = ½

Reiknivélin gefur eftirfarandi:

   3v° = cos−1 (½) = 60° + k∙360° 

     v° = 60°/3 + k∙360°/3        k er heil tala, jákvæð eða neikvæð.

     v° = 20° + k∙120°   

Ef við nú setjum k = 0, 1 og 2 fáum við eftirfarandi lausnir á bilinu :

   20°, 140° og 260°

En þetta er aðeins helmingur lausnanna. Við verðum að muna eftir reglunni cos x = cos (−x) sem lesa má úr einingarhringnum. Við þurfum því að reikna með eftirfarandi lausnum:

   3v° = cos−1 (½) = −60° + k∙360°

     v° = −60°/3 + k∙360°/3

     v° = −20° + k∙120°

Ef við nú setjum inn k = 1, 2 og 3 fáum við eftirfarandi lausnir til viðbótar:

   100°, 220° og 340°

Samtals eru lausnirnar eftirfarandi:

   20°, 100°, 140°, 220°, 260° og 340°

Við skulum nú skoða þetta á grafi. Við teiknum upp tvö föll, bylgjufallið f(v°) = 2∙cos 3v° láréttu línuna y = 1 sem mynda hægri og vinstri hlið jöfnunnar. Skurðpunktar grafanna sýnir lausnir jöfnunnar.

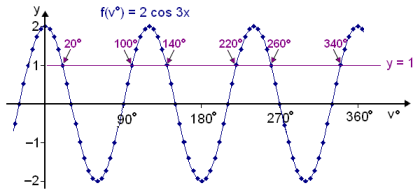
Sýnidæmi 2

Leysum jöfnuna sin x = ½ á bilinu 0 x < 4.

Notum reiknivélina.

Reiknivélin gefur hornið ekki upp sem brot af . Til þess að finna það form verðum við að stilla á gráður (deg) og breyta þeim í brot af p með því að margfalda með hlutfallinu /180°.

   x = sin−1(½) = 30°∙ p/180° = p/6

   x = p/6 + k∙2p   (+ k∙12p/6)

      = p/6, 13p/6 (25p/6, 37p/6 o.s.frv.)

 Við notum k=0 og k=1 og 2p verður samnefnt 12p/6

 

Hér höfum við fundið tvær lausnir, /6 (k = 0) og 13/6 (k = 1) en við megum ekki gleyma að reiknivélin gefur aðeins helming lausnanna.Við getum lesið af einingarhringnum að sin x = sin ( − x) og reiknivélin finnur aðeins x, ekki möguleikann ( − x).

   x = sin−1(½) = 30°∙/180° = /6

   x = − /6 + k∙2

      = 5/6 (= 150°) + k∙2

      = 5/6, 17/6 o.s.frv.

Eftirfarandi svör lenda á bilinu 0 x < 2:

   /6, 5/6, 13/6 og 17/6

Sýnidæmi 3

Leysum jöfnuna 2∙sin 4(x − /4) = 1 á bilinu 0 x < 2.

   2∙sin 4(x − /4) = 1

      sin 4(x − /4) = ½

            4(x − /4) = sin−1(½) = 30° ∙/180° = /6         

                 4x − = /6 + k∙2          

                     4x = + /6 +k∙2     

                            = 7/6 + k∙2

                         x = 7/24 + k∙/2        

 Við færum yfir, einfölldum og deilum síðan í gegn með 4.

(+ k∙12/24)

Þetta gefur x-gildin 7/24, 19/24, 31/24 og 43/24 fyrir k = 0,1, 2 og 3.

En við verðum líka að finna lausnirnar sem reiknivélin gefur ekki upp.

   4x − = ( − /6) + k∙2

         4x = 2 − /6 + k∙2

         4x = 11/6 + k∙2

           x = 11/24 + k∙/2           (+ k∙12/24)

Þetta gefur x-gildin 11/24, 23/24, 35/24 og 47/24 fyrir k = 0, 1, 2 og 3.

Samtals eru lausnirnar eftirfarandi:

7/24, 11/24, 19/24, 23/24, 31/24, 35/24, 43/24 og 47/24.

(52,6°, 67,5°, 142,5°, 172,5°, 232,5°, 262,5°, 322,5° og 352,5°.)

Teiknum nú fallið f(x) = 2∙sin 4(x − /4), línuna y = 1 og skoðum skurðpunkta þeirra.

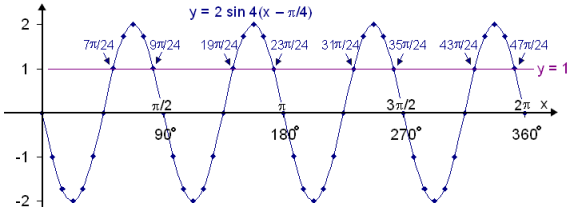
Sýnidæmi 4

Finnum nú allar lausnir á ójöfnunni cos 2x ½ á bilinu 0 x < 2.

Byrjum á því að finna allar lausnir jöfnunnar cos 2x = ½.

   2x = cos−1(½) = 60°∙/180° = /3 + k∙2

     x = /6 + k∙

 Deilum í gegn með 2

Ef við veljum k = 0 og 1 og fáum lausnirnar /6 og 7/6 (30° og 210°).

Lausnirnar sem reiknivélin finnur ekki eru neikvæða hornið með tilheyrandi endurtekningum vegna bylgjunnar
(sbr. regluna cos x = cos (−x)):

   2x = −/3 + k∙2

     x = −/6 + k∙

 Deilum í gegn með 2.

Ef við veljum nú k = 1 og 2 þá fáum við  lausnirnar 5p/6 og 11/6 (150° og 330°).

Við skulum nú teikna þetta upp til þess að átta okkur á lausn ójöfnunnar.

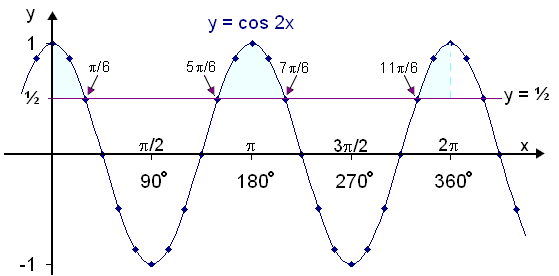
Myndin sýnir að grafið y = cos 2x er fyrir ofan línuna á þremur bilum (sjá lituð svæðin á myndinni). Þessi bil sýna jafnframt lausnir ójöfnunnar. Skilyrði ójöfnunnar eru uppfyllt ef x er á eftirfarandi bilum:

   0 x /6  eða  5/6 x 7/6  eða 11/6 x < 2

Sýnidæmi 5

Leysum ójöfnuna tan ½(x − /2) 1 á bilinu 0 x < 2.

Byrjum á jöfnunni tan ½(x − /2) = 1

   ½(x − /2) = tan−1(1) = 45°∙/180° + k∙

   ½(x − /2) = /4 + k∙    

        x − /2 = /2 + k∙2

 Margföldum í gegn með 2 og færum /2 yfir.

                 x = /2 + /2 + k∙2

                 x = + k∙2

Jafnan hefur aðeins eina lausn á bilinu 0 x < 2 og það er lausnin x = .

Teiknum nú gröf fallsins f(x) = tan ½(x − /2) og láréttu línunnar y = 1.

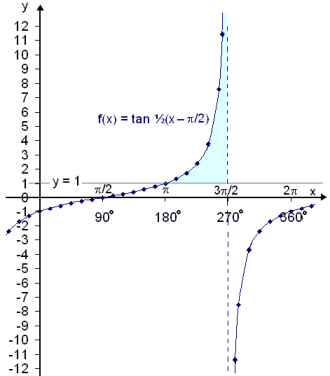
Á myndinni kemur fram að graf f(x) = tan ½(x − /2) er fyrir ofan línuna y = 1 frá x = að lóðréttu aðfellunni í 3/2
(sjá litaða svæðið á myndinni). Aðfellan sjálf er ekki með í lausninni vegna þess að þar er f(x) ekki til.
Lausn ójöfnunnar tan ½( − /2) ³ 1 er því bilið x < 3/2.

 

Æfðu þig á þessum aðferðum og taktu síðan próf 4 í hornaföllum.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum