© 2007  Rasmus ehf    og Jóhann Ísak

Hornaföll

Kynning 5   Flóknari hornafallajöfnur og ójöfnur

Sýnidæmi 1

Leysum jöfnuna sin x = cos x og í framhaldinu ójöfnuna sin x > cos x og miðum við bilið

0 x <  2p.

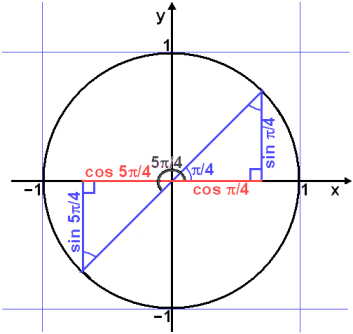
Við sjáum af einingarhringnum að sin x og cos x geta aðeins haft sama gildið á tveimur stöðum, í x = /₄ og 5/₄ (45° og 225°). Þar mynda sínus og kósínus skammhliðar í jafnarma rétthyrndum þríhyrningum.

Jöfnuna sin x = cos x getum við þar að auki leyst með því að deila í gegn með cos x.

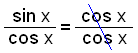
   tan x = 1

         x = tan⁻¹(1)

         x = 45°∙ /_180° + k∙

         x = /4 + k∙        (k er heil tala, jákvæð eða neikvæð)

Ef við setjum inn k = 0 og k = 1 þá fáum við lausnirnar /₄ (45°) og /₄ + = 5/₄ (45°+ 180°= 225°).

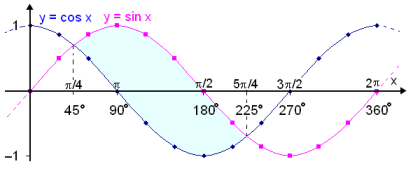
Þegar við leysum ójöfnuna sin x > cos x þurfum við að skoða hvor gefur hærra gildi sin x eða cos x á þeim bilum sem lausnirnar /₄ og 5/4 afmarka. Lausnin kemur þó greinilegast fram á eftirfarandi grafi sem sýnir gröf fallanna f(x) = sin x og g(x) = cos x. Graf sin x er fyrir ofan graf cos x á bilinu /₄   ^5x/₄ (sjá litaða svæðið á myndinni).

Lausn ójöfnunnar sin x  cos x er bilið /₄ x ^5x/₄.

Sýnidæmi 2

Leysum jöfnuna sin x ∙ cos x = 0 og síðan ójöfnuna

Jafnan hefur lausn þar sem sin x eða cos x tekur gildið 0. Við getum lesið það af einingarhringnum að sin x og cos x verða núll til skiptis á 90° fresti.

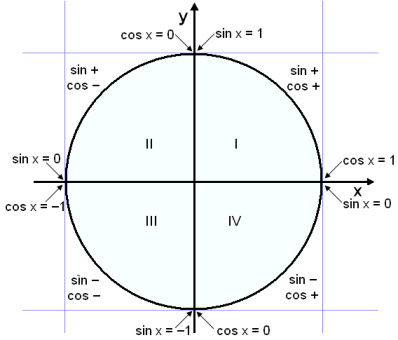
Lausnir jöfnunnar sin x ∙ cos x = 0 á bilinu 0 x < 2 eru því      0, /₂, og 3/₂ (0°, 90°, 180° og 270°).

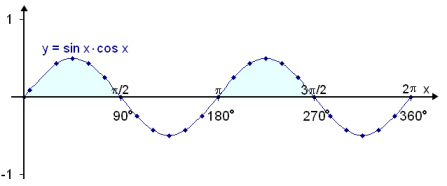
Lausn ójöfnunnar sin x ∙ cos x > 0 má einnig lesa af einingarhringnum. Lausn ójöfnunnar felst í því að finna hvar margfeldi sin x og cos x er jákvætt. Við þurfum því að finna hvar sin x og cos x hafa sama formerki. Það er aðeins í fjórðungum I og III í einingarhringnum. Lausnirnar eru því bilin 0 < x < /₂ og < x < 3/₂.

Við skulum að lokum skoða þetta á grafi.

Sýnidæmi 3

Leysum nú jöfnuna sin x ∙ cos x − sinx = 0 og síðan ójöfnuna  sin x ∙ cos x − sin x > 0 á bilinu 0  x < 2.

Jafnan hefur lausn þar sem sin x er núll eða þar sem sviginn (cos x − 1) er núll.

   sin x = 0

         x = 0 eða (180°).

eða

   cos x − 1 = 0

   cos x = 1

          x = 0

Jafnan hefur því aðeins lausnirnar 0 og p.

Skoðum þá ójöfnuna sin x ∙ cos x − sin x > 0 sem má umrita á formið sin x (cos x − 1) > 0.

Nú þurfum við að skoða formerki sin x og cos x − 1.

Setjum upp formerkjakönnun.

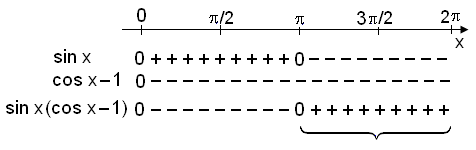
                                                                                          lausn

Við sjáum að lausnin er þar sem báðir þættir eru neikvæðir og það er á bilinu < x < 2.

Skoðum að lokum grafið fyrir forvitnissakir.

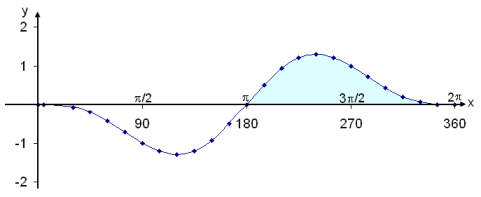
Litaða svæðið sýnir hvar grafið er fyrir ofan  x-ásinn (jákvætt) en þar er einmitt lausn ójöfnunnar.

Sýnidæmi 4

Finnum allar lausnir jöfnunnar cos² x − cos x = 0.

       cos² x − cos x = 0

    cos x∙(cos x − 1) = 0

Lausnirnar eru þar sem cos x = 0 eða cos x − 1 = 0

    cos x = 0

           x = /₂ eða 3/₂ (90° eða 270°)

           x = /₂ + k∙

eða

   cos x − 1 = 0

         cos x = 1

                x = 0 + k∙2 = k∙2

Allar lausnir má tjá með stæðunni x = /₂ + k∙

Sýnidæmi 5

Finnum allar lausnir jöfnunnar sin² x − 5 sin x + 4 = 0.

Þetta jafna af öðru stigi með óþekktu stærðina fólgna í sin x.

Hér notum við annars stigs jöfnuna þar sem a = 1, b = −5 og c = 4.

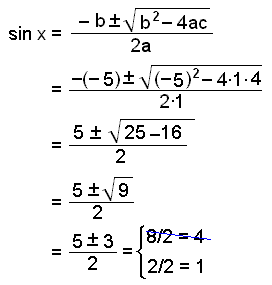
Sínus getur ekki tekið gildið 4 þannig að sin x = 4 strikast út. Þá er eini möguleikinn sem eftir er sin x = 1 sem hefur aðeins lausnina /₂ (90°). Svarið verður því eftirfarandi:

   x = /₂ + k∙2

Sýnidæmi 6

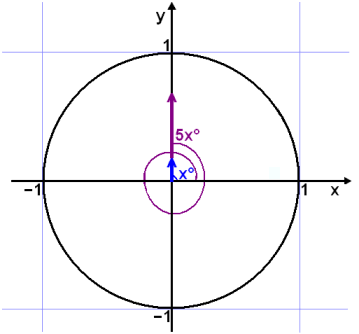
Leysum jöfnuna sin 5x° = sin x°.

Stefnan 5x° hlýtur að vera sú sama og stefnan x° og síðan hlýtur staðan að endurtaka sig einu sinni á hverjum hring sem bætt er við (eða dreginn er frá). Við fáum því eftirfarandi jöfnu:

1)  5x° = x° + k∙360°

      4x° = k∙360°

Staðan er þá eins og myndin hér fyrir neðan sýnir. Þessi lausn inniheldur fyrri lausnir þannig að við getum sett fram endanlega lausn á eftirfarandi hátt:         

 x° = k∙90°

Sýnidæmi 7

Leysum jöfnuna cos 2x = cos x á bilinu 0   x < 2.

1)   Fyrri möguleikinn byggir á því að sama stefnan eigi við á báðum hliðum jöfnunnar.

2x = x + k∙2            x = k∙2               x = 0

Við drögum x frá báðum hliðum og veljum k = 0 (k = 1 gefur 2 sem er of hátt).

2)  Seinni möguleikinn byggir á því að sama kósínus má lesa af einingarhringnum fyrir jákvæð og neikvæð horn. Reglan er cos v = cos (−v) og lausnin verður eftirfarandi:

           2x = −x + k∙2

           3x = k∙2

             x = k∙2/₃

Þetta gefur lausnirnar 2/₃ (120°) fyrir k = 1 og 4/₃ (240°) fyrir k = 2.

Lausnirnar eru því samtals þrjár, 0, 2/₃ og 4/3.

Sýnidæmi 8

Leysum jöfnuna tan 3x = tan 2x.

Þessi gerð af jöfnu er að mörgu leyti einfaldari en jöfnur með sínus og kósínus. Hér þurfum við aðeins að reikna með því að tan x endurtekur sig á 180° fresti.

   3x = x + k∙180°

     2x = k∙180°

       x = k∙90°

eða í radíönum

     x = k∙/₂

Æfðu þig á þessum aðferðum og taktu síðan próf 5 í hornaföllum.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum