© 2008 Rasmus ehf og Jóhann Ísak
© 2008 Rasmus ehf og Jóhann Ísak |
Föll I |
|
Skoðum nokkrar einfaldar jöfnur sem sýna tengsl tveggja breyta x og y og skoðum einnig fyrir hvaða punkta í hnitakerfinu þessi tengsl gilda.
Við skulum velja x-gildin −2, −1, 0, 1 og 2, reikna y-gildin út frá þeim og setja upp í svokallaða gildistöflu.
Skoðum jöfnuna y = 2x + 4.
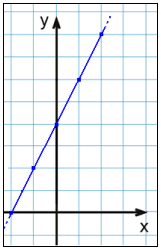
Við reiknum fyrst út gildistöfluna. Setjum síðan punktana upp í hnitakerfi og tengjum þá loks saman með beinni línu.
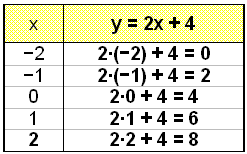 |
 |
Þetta er sérlega fljótlegt að gera í grafískum reiknivélum. Í reiknivél af gerðinni CASIO er þetta t.d. gert með því að velja TABLE á aðalvalmyndinni.


Í næstu valmynd þarf að skrifa inn fallið (table func) Y1=2x+4.
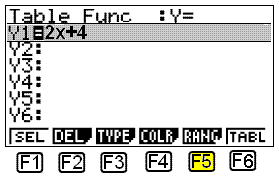
Nú þarf að ákveða á hvaða bili tölurnar eiga að vera. Til þess veljum við „RANGE“ með F5. Þá fáum við upp eftirfarandi valmynd:
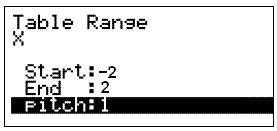
Hér veljum við byrjunina (start) −2 og endinn (end) 2 og skrefastærðina (pitch) 1. Þetta má gera með eftirfarandi runu af aðgerðum:
![]()
Nú förum við sjálfkrafa til baka í fyrri valmynd þar sem við veljum „TABLE“ með F6. Gildistaflan birtist þá og verður eins á myndinni hér fyrir neðan:
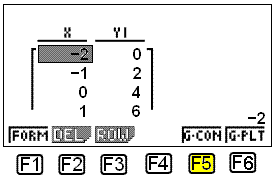
Grafið má síðan teikna upp með því að velja „G-CON“ með F5 (prófaðu þetta).
Það má einnig teikna gröf í töflureikninum EXCEL. ![]()
Ræstu upp Excel forritið og gerðu eftirfarandi tilraunir:
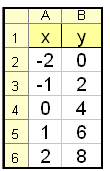
Þá skrifum við −2 og −1 í reiti A2 og A3 (sjá EXCEL-töfluna hér fyrir ofan), en afganginn af A-dálkinum getum við fengið með því að „blokka“ bæði A2 og A3 og afrita síðan niður. Formúlan í B2 verður =2*A2+4 og hana má afrita niður.
Grafið gerum við síðan með því að velja línuritastikuna (1) |
|
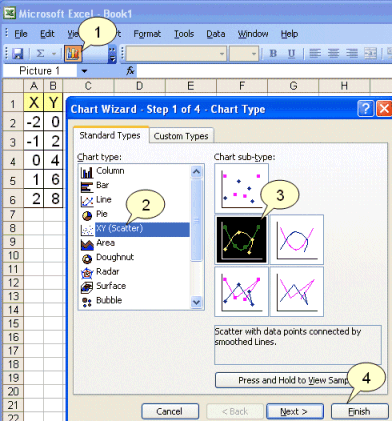 |
Síðan veljum við „xy-scatter“ (2) |
Þá samhangandi graf með punktum (3) |
|
|
og velja loks að ljúka (4) |
Grafið sem kemur verður línustrikað og kvarðinn á ásunum annar en á myndinni hér fyrir ofan. Þetta getum við lagað með því að hægrismella á þau atriði í grafinu sem við viljum bæta og breyta þeim.
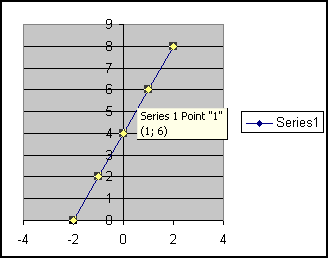
Skoðum fleiri dæmi.
Setjum upp gildistöflur og skoðum gröf eftirfarandi falla:
y = x |
||
| x | y = x | 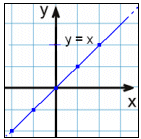 |
| -2 | -2 | |
| -1 | -1 | |
| 0 | 0 | |
| 1 | 1 | |
| 2 | 2 | |
y = 2 |
||
|
x |
y = 2 |
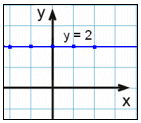 |
| -2 | 2 | |
| -1 | 2 | |
| 0 | 2 | |
| 1 | 2 | |
| 2 | 2 | |
y = x2 |
||
| x | y = x2 | 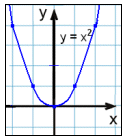 |
| -2 | 4 | |
| -1 | 1 | |
| 0 | 0 | |
| 1 | 1 | |
| 2 | 4 | |
y = 2x |
||
|
x |
y = 2x | 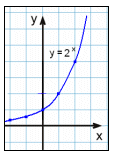 |
| -2 | 1/4 | |
| -1 | 1/2 | |
| 0 | 1 | |
| 1 | 2 | |
| 2 | 4 | |
Við skulum nú skoða nokkrar jöfnur sem lýsa samhengi á milli x og y sem ekki er hægt að reikna út án umhugsunar og teikna síðan upp.
x = 2
Ef það er eina skilyrðið að x hafi gildið 2 þá skiptir engu máli hvaða gildi y hefur. Við getum valið gildin −2, −1, 0, 1 og 2 og sett upp eftirfarandi gildistöflu:
|
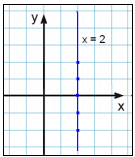 |
Niðurstaðan er lóðrétt lína í gegnum 2 á x-ás.
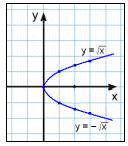
Skoðum næst sambandið y2 = x.
Hér getum við leyst jöfnuna með tilliti til y sem gefur
y = ±![]()
Nú fáum við tvö svör fyrir hvert x og þar fyrir utan getum við ekki sett inn neikvæð gildi á x (ekki er hægt að draga ferningsrót af neikvæðri tölu). Við setjum samt sem áður upp gildistöflu og teiknum graf.
 |
 |
Skoðum að lokum jöfnuna x2 + y2 = 4.
Leysum jöfnuna með tilliti til y.
x2 + y2 = 4
y2 = 4 − x2
![]()
Enn fáum við tvær lausnir fyrir hvert gildi á x og við komumst fljótt að raun um það að x-gildin sem við setjum inn í jöfnuna verða að vera undir 2 og yfir −2 eða á bilinu [−2, 2], annars verður stærðin undir rótarmerkinu neikvæð. Við skulum setja þetta upp í gildistöflu og skoða niðurstöðuna á grafi.
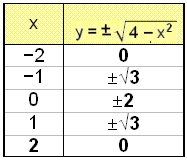 |
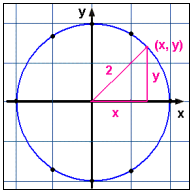 |
Punktarnir sem við fáum raða sér á hring með miðju í (0, 0) og með radíus 2.
Það er eðlileg niðurstaða vegna þess að jafnan x2 + y2 = 4 er í raun Pýþagórasarregla sem gefur lengdina 2 á langhlið rétthyrnds þríhyrnings með skammhliðarnar x og y. Þessi skilningur á jöfnunni gefur okkur þá sýn að punktar með hnitin (x, y) sem uppfylla skilyrði jöfnunnar hljóta allir að vera í fjarlægðinni 2 frá miðju hnitakerfisins og mynda því hring með radíus 2.
Þessi dæmi sýna að hér er dálítill eðlismunur á. Ef við höfum eitt ákveðið samband á milli x og y, t.d. formúlu sem gefur eitt gildi á y fyrir hvert og eitt gildi á x sem sett er inn, þá getum við reiknað út einfalda gildistöflu og teiknað graf án mikilla tilfæringa. Samband af þessu tagi nefnist fall og sagt er „y er fall af x“ (oft skrifað y = f(x)).
Reikniregla eða hvers konar aðgerð sem gefur nákvæmlega eitt gildi á y fyrir hvert gildi á x nefnist fall.
Gröf falla eru þannig að ekki er hægt að finna neina lóðrétta línu sem sker grafið oftar en einu sinni.
Við skulum skoða þetta á mynd af gröfum úr sýnidæmunum hér á undan.
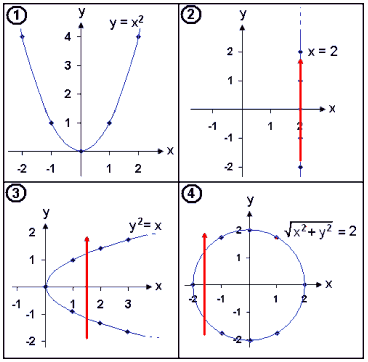
Rauðu lóðréttu örvarnar skera gröf 2, 3 og 4 í fleiri en einum punkti sem gefur til kynna að þau séu ekki gröf falla. Aftur á móti er ekki hægt að finna nokkra lóðrétta ör sem sker graf 1 oftar en einu sinni enda tjáir jafnan y = x2 fall.
Föll eins og y = x2 eru jafnan táknuð með bókstöfum. Þannig getum við sagt y = f(x) (lesið y er fall af x) og þá er átt við að f er einhver formúla með breytunni x. Þá er sagt f(x) = x2 (fallið af x er x í öðru veldi). Einnig getum við sagt að f af 2 eru 4 vegna þess að tveir hafnir í annað veldi eru 4. Á táknmáli stærðfræðinnar er þetta skrifað f(2) = 22 = 4.
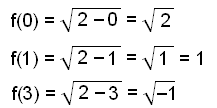 |
Við setjum 0,1 og 3 inn fyrir x og reiknum út gildin á f(x) |
Hér neðst ef x = 3 gengur það ekki . Kvaðratrót af neikvæðri tölu er ekki til í okkar talnakerfi. |
|
Föll gilda einnig fyrir bókstafi. Ef f(x) = x3 + x2 þá er f(a) = a3 + a2 og f(a2) = a6 + a4 og f(a+1) = (a+1)3 + (a+1)2.
Gefið er fallið f(x) = x2. Finnum f(a), f(2a), f(a+1) og f(a+b).
f(a) = a2
f(2a) = 4a2
f(a+1) = (a+1)2 = a2 + 2a + 1
f(a+b) = (a+b)2 = a2 + 2ab + b2
Æfðu þig á þessum aðferðum og taktu síðan próf
1 í föllum.
ps. mundu eftir að fylla út í tékklistann þinn jafnóðum