Rasmus ehf, Föll kynning 2

Föll I

Kynning 2 Margliður

Eftirfarandi föll nefnast margliður:

Stig	f(x)	dæmi um graf:
0	f(x) = a Stuðull: a
1	f(x) = ax+b Stuðlar: a og b
2	f(x) = ax²+bx+c Stuðlar: a, b og c
3	f(x) = ax³+bx²+cx+d Stuðlar: a, b, c og d
4	f(x) = ax⁴+bx³+cx²+dx+e Stuðlar: a, b, c, d og e
O.s.frv

Stuðlarnir a, b, c, o.s.frv. eru tölur sem eru einkennandi fyrir hverja margliðu en x er breyta. Liðunum er raðað eftir lækkandi veldum á x og hæsta veldið ákveður stig margliðunnar. Ef einhvern lið vantar í röðina þá er það vegna þess að viðkomandi stuðull er 0. Ef hins vegar stuðul vantar þá er það vegna þess að hann er í raun talan 1 og skiptir því ekki máli (og er þá ekki skrifaður).

Sýnidæmi 1

Finnum stig og stuðla í eftirfarandi margliðu:

f(x) = x⁵ − 2x³ + 4x − 5

Hæsta veldið er 5 þannig að stigið er fimmta stig (eða gráða). x⁴ og x² vantar þannig að stuðlarnir við þau veldi eru 0. Enginn stuðull er við x⁵ þannig að stuðullinn við það veldi er 1. Við getum einnig hugsað okkur að aftasti liðurinn tilheyri x⁰, en allar tölur í veldinu 0 eru jafnar einum svo það breytir ekki neinu. Við getum því umritað margliðuna á eftirfarandi form og lesið af stuðlana:

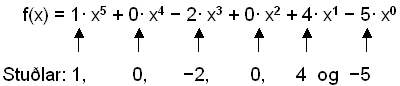
Veldin í margliðum verða að vera heilar, jákvæðar tölur eða 0 (í menginu N₀). Eftirfarandi föll eru ekki margliður

f(x) = x² + x + 1 + x⁻¹ + x⁻²	(neikvæð veldi á x)
g(x) = x² + x + 1 + Öx	(x er undir ferningsrót)
h(x) = x² + x + 1 + 2^x	(x er í veldisvísi)
	(x er undir striki)

Eins og kemur fram á myndunum hér fyrir ofan þá er margliða af stiginu 0 lárétt lína. Fyrsta stigs margliða er hins vegar hallandi lína og annars stigs margliða myndar bogadreginn sveig sem nefnist fleygbogi. Þriðja stigs margliða myndar graf sem er eins konar samsuða úr tveimur fleygbogum sem snúa í sitt hvora áttina. Fjórða stigs margliða er oftast eins konar samsuða úr þremur fleygbogum og fimmta stigs úr fjórum og þannig koll af kolli. Með hækkandi gráðu fjölgar bugðunum.
Þetta hefur í för með sér að fyrsta stigs margliða sker x-ásinn aðeins einu sinni, annars stigs margliða í mesta lagi tvisvar sinnum, þriðja stigs margliða í mesta lagi þrisvar o.s.frv. Af þessu drögum við réttilega þá ályktun að gráðan segi til um það hve oft graf tiltekinna margliða geti skorið x-ásinn (skoðaðu gröfin aftur).

Töluliðurinn í hverri margliðu segir til um hvar hún sker y-ásinn þar er x-hnitið 0 (x-hnit allra punkta á y-ás eru 0). Þannig að ef við setjum 0 inn fyrir x t.d. í jöfnunni

f(x) = 2x³+ 3x²+ 4x + 6 verður það

f(0) = 2∙0³+ 3∙0²+ 4∙0 + 6 = 6

Punkturinn (0, 6) er á grafinu og y-ásnum.

Með sömu hugsun getum við fundið skurðpunkta grafsins og x-ássins.

Á x-ásnum eru öll y-hnit (hæðin) núll. Við getum því fundið skurðpunktana með því að leysa jöfnuna y = f(x) = 0.

Sýnidæmi 2

Finnum skurðpunkta margliðunnar f(x) = 2x + 4 við ása hnitakerfisins.

y-skurður er 4.	Síðasti tölustuðullin er 4.
2x + 4 = 0	Setjum f(x) = 0.
x = ⁻⁴/₂ = −2	Leysum fyrir x.
x-skurður er −2.

Sýnidæmi 3

Finnum skurðpunkta margliðunnar f(x) = x² − 2x við ása hnitakerfisins.

y-skurður er 0.	Síðasti tölustuðullin er 0.
x² − 2x = 0	Setjum f(x) = 0.
x (x − 2) = 0	Þáttum og leysum fyrir x.
x-skurður er í 0 og 2.

Sýnidæmi 4

Finnum skurðpunkta margliðunnar f(x) = (x − 1)(x − 2)(x − 3) við ása hnitakerfisins.

Hér getum við margfaldað svigana fyrst saman til þess að finna síðasta tölustuðulinn.

(x − 1)(x − 2)(x − 3) = (x² − 2x − x + 2)(x − 3)

= (x² −3x + 2)(x − 3)

= x³ − 3x² − 3x² + 9x + 2x − 6

= x³ − 6x² + 11x − 6

Einfaldara er þó að finna f(0), en það gefur y-skurðinn.

f(0) = (0 − 1)(0 − 2)(0 − 3) = −6

Skurðpunkturinn er í y = −6.

Til þess að finna hvar grafið sker x-ásinn leysum við jöfnuna

(x − 1)(x − 2)(x − 3) = 0

Þessi stæða verður 0 þegar hver og einn sviganna verður 0 en einmitt þá verður öll stæðan 0. Lausnirnar verða 1, 2 og 3 og á þeim stöðum sker grafið x-ásinn.

Sýnidæmi 5

Athugum hvort punktarnir (1, 6) og (2, 8) eru á grafi fallsins f(x) = x² + 4x + 1.

f(1) = 1² + 4∙1 + 1	Setjum 1 inn fyrir x og reiknum
= 1 + 4 + 1 = 6

(1, 6) er á grafinu.

f(2) = 2² + 4∙2 + 1

= 4 + 8 + 1 = 13

(2, 8) er ekki á grafinu.

Sýnidæmi 6

Finnu margliðu af fyrstu gráðu (línu) sem sker punktana (1, 1) og (2, 3).

Köllum fallið f(x) = ax + b

f(1) = a∙1 + b = 1 gefur jöfnuna a + b = 1	Setjum 1 inn.
f(2) = a∙2 + b = 3 gefur jöfnuna 2a + b = 3	Setjum 2 inn.
f(2) − f(1) = (2a + b) − (a + b) = 3 − 1 = 2a + b − a − b = 2 a = 2 2 + b = 1 b = 1 − 2 = −1	Leysum jöfnuhneppið a + b = 1 2a + b = 3

Jafna margliðunnar (línunnar) er f(x) = 2x − 1.

( Sjá nánar aðra úfærslu með notkun á hallatölu í liðnum Hnitakerfi 1 Kynning 3 )

Sýnidæmi 7

Finnu margliðu af öðru stigi (fleygboga) sem sker punktana (0, 6), (1, 0) og (3, 0).

Köllum fallið f(x) = ax² + bx + c

(0, 6) er y-skurður grafsins þannig að c = 6.

f(1) = a∙1² + b∙1 + 6

= a + b + 6 = 0

f(3) = a∙3² + b∙3 + 6 = 0
= 9a + 3b + 6 = 0
3a + b + 2 = 0

Einföldum jöfnuna með því að deila í gegn með 3.

f(3) = f(1) = 0
       3a + b + 2 = a + b + 6
       3a − a + b − b = 6 − 2
       2a = 4
       a = 2

f(1) = 2 + b + 6 = 0
b = −2 − 6 = −8

Margliðan er f(x) = 2x² − 8x + 6

Æfðu þig á þessum aðferðum og taktu síðan próf 2 í föllum.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum