© 2008  Rasmus ehf    og Jóhann Ísak

Föll I

Kynning 3      Annars stigs fallið

Skoðum nánar annars stigs margliður. Einfaldasta formið er fallið f(x) = x², en grafið er svokallaður fleygbogi.

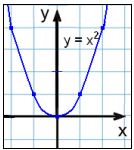
Við tökum eftir því að fallið myndar spegilmynd af sjálfu sér um y-ásinn. „Grafið er samhverft um y-ásinn“ kallast það og y-ásinn er samhverfuás grafsins.

Við skulum nú skoða hvernig hægt er að fá misgleiða fleygboga með því að margfalda fallið með mismunandi stuðlum. Stuðullinn við x² er oftast táknaður með bókstafnum a. Hér fyrir neðan tekur a gildið 4, 2, ½ og ¼.

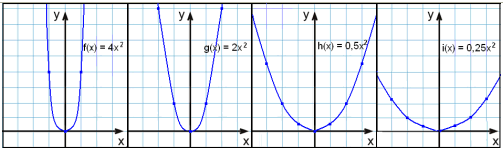
         a = 4                a = 2                a = ½               a = ¼

Lítum nú á hvað gerist ef a fer niður fyrir 0 og verður neikvæð stærð.

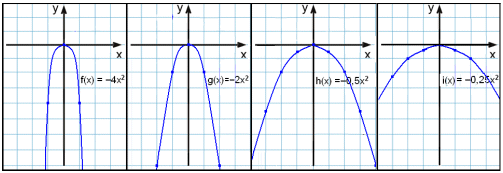
        a = −4              a = −2              a = −½             a = −¼   

Um graf af gerðinni y = ax² gildir að það er hvass fleygbogi sem vísar upp á við ef a er stór jákvæð tala. Ef a minnkar og nálgast 0 þá verður fleygboginn gleiðari og ef a fer niður fyrir 0 þá snýst hann við.

Sýnidæmi 1

Teiknum grafið f(x) = x² + 1 og berum það saman við g(x) = x².

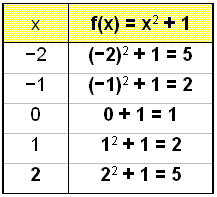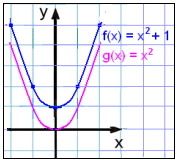Tölurnar í gildistöflunni hafa allar hækkað um einn miðað við g(x) = x² og grafið hefur því hliðrast upp um eina einingu.

Taktu eftir því að grafið f(x) = x² + 1 sker ekki x-ásinn. Það merkir að jafnan x² + 1 = 0 hefur enga lausn, enda verða öll neikvæð x gildi jákvæð við það að hefjast í annað veldi þannig að ekkert getur dregist frá. Stærðin x² + 1 verður alltaf stærri en núll.

Sýnidæmi 2

Skoðum nú grafið f(x) = x² − 1 og berum það saman við grafið g(x) = x².

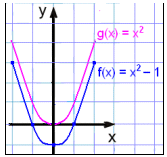Tölurnar í gildistöflunni hafa allar lækkað um einn miðað við g(x) = x² og grafið hefur því hliðrast niður um eina einingu.

Taktu eftir því að grafið f(x) = x² − 1 sker x-ásinn í tveimur punktum. Það merkir að jafnan x² − 1 = 0 hefur tvær lausnir,

x² − 1 = 0

       x² = 1

         x = ±1

sem eru x = −1 og x = 1.

Sýnidæmi 3

Skoðum nú grafið f(x) = (x + 1)² (eða f(x) = x² + 2x + 1) og berum það saman við g(x) = x².

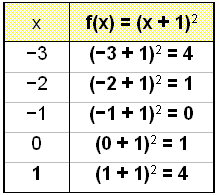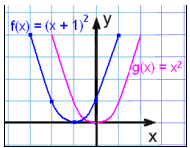Hér höfum við bætt einum við x . Það kemur út eins og grafinu g(x) = x² hafi verið hliðrað um einn til vinstri. Samhverfuásinn er nú í x = −1.

Sýnidæmi 4

Teiknum nú grafið f(x) = (x − 2)² − 1 (eða f(x) = x² − 4x + 3) og berum það saman við g(x) = x². Ef við miðum við sýnidæmin hér á undan þá hliðrast fleygboginn nú um tvo reiti til hægri og einn niður. Við byrjum því gildistöfluna á x = 0.

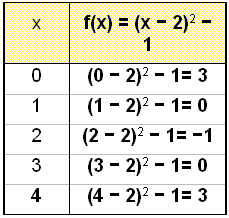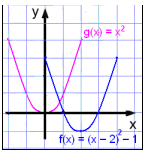Taktu eftir því að samhverfuásinn er nú x = 2. Taktu einnig eftir því að skurðpunktinn við y-ásinn getum við fundið án þess að teikna grafið. Það er gert með því reikna út f(0) = 3 eða margfalda upp svigann og lesa af tölustuðulinn aftast (þegar x verður 0 þá detta allir liðir út nema tölustuðullinn aftast).

f(x) = (x − 2)² − 1 = x² − 4x + 4 − 1 = x² − 4x + 3

    eða    f(0) = (x − 2)² − 1 = 4 − 1 = 3

Sýnidæmi 5

Finnum nú skurðpunkta grafsins f(x) = (x − 2)² − 1 við x ásinn. Aftur setjum við y = f(x) = 0 og leysum síðan jöfnuna.

Skurðpunktarnir eru í x = 2 −1 = 1 og í x = 2 + 1 = 3.

Ljóst er að formið f(x) = (x − 2)² − 1 er mjög upplýsandi. Það segir til um hve mikið grafið hefur hliðrast til hliðar og niður (eða upp). Af þessu formi má einnig lesa samhverfuásinn og reikna út skurðpunkta grafsins við ása hnitakerfisins. Almennt verður þetta form eftirfarandi:

    f(x) = a(x + r)² + s

Stuðullinn a er tölustuðullinn við x².

Samhverfuásinn verður samkvæmt þessu x = −r (eða r með öfugu formerki).

Mikilvægt er að kunna að umrita venjulegt margliðuform yfir á umrætt lausnarform.

    f(x) = ax² + bx + c yfir á f(x) = a(x + r)² + s

Sýnidæmi 6

En skoðum nú hvernig hægt er að koma falli á venjulegu margliðuformi yfir á umrætt lausnarform. Tökum dæmi sem við þekkjum eða f(x) = x² − 4x + 3 yfir á formið f(x) = (x − 2)² − 1. Berum saman:

    f(x) = ax² + bx + c

    f(x) = x² − 4x + 3

Hér er a = 1

    og b = −4

    og c = 3 (þannig að grafið sker y-ás í 3).

Berum þetta saman við regluna (x ± q)² = x² ± 2qx + q².

Við sjáum að stuðullinn við x er 2q og hálfur stuðullinn við x er q sem er síðan í öðru veldi aftast í reglunni. Í okkar tilfelli í margliðunni f(x) = x² − 4x + 3 þyrfti aftasti stuðullinn að vera 2² eða 4 ef við vildum nýta okkur regluna til þess að búa til sviga í öðru veldi. En við getum bætt 4 inn í dæmið og dregið það frá á eftir ef okkur sýnist svo. Við getum hæglega bætt inn hvaða q² sem er ef við drögum það frá aftur. Reynum þetta:

Af dæminu hér fyrir ofan getum við dregið þá ályktun að graf margliðu af öðru stigi (f(x) = x² + bx + c) hafi

    samhverfuás í x = ^−b/₂ (ef a = 1) og skeri y-ás í y = c.

Sýnidæmi 7

Finnum samhverfuás grafsins f(x) = 2x² − 12x + 10.

Hér er a = 2 þannig að við getum ekki treyst því að aðferðin í sýnidæminu hér að framan dugi. Það er heldur ekki auðvelt að umrita þessa stæðu. Ef við hins vegar hliðrum henni niður um 10 einingar þá fáum við fallið g(x) = 2x² − 12x sem hefur sama samhverfuás og f(x).

Finnum nú hvar g(x) sker x-ásinn.

    2x² − 12x = 0

    2x(x − 6) = 0

Þessi stæða verður 0 ef x = 0 eða 6. Grafið sker því x-ás í 0 og 6 og samhverfuásinn er þar mitt á milli eða í x = 3.

Sýnidæmi 8

Reynum nú að búa til lausnarformið a(x + r)² + s úr margliðunni

Af þessu getum við lesið að samhverfuásinn er í x = 3.

Í dæminu hér fyrir ofan (f(x) = 2x² − 12x + 10) eru stuðlarnir a = 2, b = −12 og c = 10. Þegar við fundum samhverfuásinn tókum við fyrst a = 2 út fyrir sviga sem jafngildir deilingu með a = 2. Loks deildum við útkomunni (6) með tveimur og skiptum um formerki.

Almenn formúla fyrir samhverfuás f(x) = ax² + bx + c er því eftirfarandi:

Sýnidæmi 9

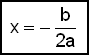
Finnum nú botnpunkt grafsins f(x) = 2x² − 12x + 10.

Við vitum að botnpunkturinn er á samhverfuás fleygbogans í x = 3. y-hnitið er f(3) = 2∙3² − 12∙3 + 10 = 18 − 36 + 10 = −8.

Botnpunkturinn er (3, −8).

Taktu eftir því að ef stuðullinn a er neikvæður (a < 0) þá svignar fleygboginn niður á við og hefur topppunkt en ekki botnpunkt.

Æfðu þig á þessum aðferðum og taktu síðan próf 3  í föllum 1.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum