© 2008  Rasmus ehf    og Jóhann Ísak Pétursson

Föll I

Kynning 5      Formengi og varpmengi falla

Við getum ímyndað okkur fall sem eins konar vél eða aðgerðaröð sem tekur inn ákveðnar tölur (formengi) og skilar af sér útkomutölum (varpmengi). Við höfum kynnst því að sum föll geta ekki tekið við öllum tölum og það eru einnig takmarkanir á því hvaða tölur geta komið út.

Þær tölur (þau x) sem við ákveðum að formúlan f(x) gildi fyrir nefnum við formengi f og táknum það með F_f. (Ef við kjósum að kalla fallið g(x) þá verður formengið F_g ). Ef formengi er ekki tilgreint gerum við ráð fyrir að formúlan gildi fyrir allar tölur í mengi rauntalna (menginu R).

Við skulum nú hugsa okkur að allar tölurnar í hinu valda formengi fari í gegnum þær aðgerðir sem fallið f(x) býður. Útkomurnar mynda þá mengi sem við köllum varpmengi og er táknað með V_f. Vörpun er annað nafn á falli og sem byggir á þeirri hugsun að tölur úr formenginu varpist yfir á tölur í varpmenginu.

Þegar við ákveðum formengi falla verðum við að taka tillit til þess að reikningsaðgerðirnar geta reist okkur skorður varðandi hvaða tölur við notum. Helstu takmarkandi reikningsaðgerðir eru deiling og ferningsrætur (eða aðrar jafntölurætur). Við verðum að velja burt þær tölur sem valda deilingu með núlli eða ferningsrót af neikvæðri tölu.

Það getur verið vandasamara að finna varpmengi falla. Einfaldasta ráðið er að skoða grafið og reyna að lesa af því takmörk varpmengisins. Einnig getum við reiknað gildi fyrir útmörk formengisins og reynt að áætla hvað gerist þar á milli.

Sýnidæmi 1

Skoðum fallið f(x) = 2x + 4. Við sjáum að við þurfum ekkert að takmarka formengið. Allar tölur ganga. Við setjum því F_f = R.

Þegar við setjum upp í gildistöflu getum við hugsað okkur að við veljum nokkrar tölur úr formenginu í dálkinn vinstra megin og reiknum. Niðurstöðurnar (y) koma í dálkinn hægra megin og verða eins konar sýnishorn úr varpmenginu. Við sjáum fljótlega að við getum fengið út hvaða tölu sem er, jafnt stórar sem smáar. Grafið sýnir beina línu sem við getum framlengt endalaust upp eða niður. Varpmengið nær því yfir allar tölur og er skrifað V_f = R.

Sýnidæmi 2

Við skulum næst líta á fallið

Við sjáum fljótlega að 0 gengur ekki þannig að formengið verður R\{0}.

Varpmengið er ekki eins ljóst. Við getum ekki fundið neina lausn á jöfnunni ¹/x² = 0 þannig að fallið sker ekki x-ásinn. Hins vegar er f(10) = f(−10) = ¹/100 og f(100) = f(−100) = ¹/10.000 o.s.frv. þannig að grafið nálgast stöðugt x-ásinn þegar fjær dregur núlli, en verður þó aldrei 0 eða neikvætt. Eins rýkur grafið upp úr öllu valdi þegar við nálgumst 0. T.d. er f(¹/10) = f(⁻¹/10) = 100 og f(¹/100) = f(⁻¹/100) = 10.000. Varpmengið nær því yfir allar jákvæðar tölur frá 0 og upp úr. V_f = á0, ®ñ.

Sýnidæmi 3

Skoðum nú fallið

Ljóst er að formúlan tekur við öllum tölum nema x = 2 þannig að formengið er F_f = R\{2}.

Af grafinu og gildistöflunni sjáum við að engar útkomur eru á bilinu frá −2 upp í 2 þannig að varpmengið er

V_f = {y Î R│y £ −2 eða y ³ 2}.

Sýnidæmi 4

Lítum að nú á fleygbogann y = x² − 2x + 2.

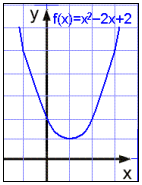
Við vitum að boginn svignar upp (a > 0) og hefur því botnpunkt og varpmengið er frá botnpunktinum og þaðan upp í óendanleikann. Við verðum því að finna botnpunktinn til þess að ákvarða varpmengið. Við notum okkur að samhverfuásinn er í x = ^−b/_2a.

x-hnitið verður x = −(⁻²/₂) = 1.

y-hnitið reiknum við síðan með formúlunni f(x).

f(1) = 1 − 2∙1 + 2 = 1. Botnpunkturinn er (1, 1) og V_f = [1, ®ñ.

Sýnidæmi 5

Skoðum að lokum fallið

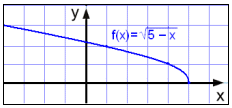Við sjáum að x má ekki verða stærra en 5. Eftir það verður útkoman undir ferningsrótinni neikvæð. Við getum hins vegar valið hvaða neikvæða x sem er (vegna þess að þá verður tvöfaldur mínus (−− = +) undir ferningsrótinni). Formengið er því eftirfarandi:

Til þess að finna varpmengið er rétt að setja upp gildistöflu og skoða grafið.

Við sjáum að grafið endar í punktinum (5, 0). Aftur á móti getum við haldið áfram með grafið á ská upp til vinstri eins langt og við kærum okkur um. Varpmengið er því eftirfarandi:

Hafðu í huga að við miðum formengið við x-ásinn en varpmengið við y-ásinn.

Æfðu þig á þessum aðferðum og taktu síðan próf 5 í föllum 1.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum