© 2008  Rasmus ehf    og Jóhann Ísak

Föll 2

Kynning 4

Hágildi, lággildi og könnun falla með hjálp afleiðu

Afleiða segir til um halla falls. Því er eðlilegt að álykta eftirfarandi.

Við getum í framhaldi af þessu ályktað að þar sem afleiðan skiptir um formerki hlýtur að vera botnpunktur eða topppunktur á grafinu. Þessir punktar þurfa hins vegar ekki endilega að vera lægstu eða hæstu punktar grafsins. Þess vegna er oft talað um staðbundið hágildi eða staðbundið lággildi.

Formerkjakönnun á afleiðu gefur upplýsingar um hvar fall er vaxandi, hvar það er minnkandi, hvar staðbundin hágildi og hvar staðbundin lággildi er að finna.

Við skulum hafa í huga að samfellt fall getur ekki skipt um formerki nema að hafa einhvers staðar gildið 0. Þetta hefur í för með sér að við getum leitað að staðbundnum hágildum og lággildum þar sem afleiðan er 0. Við þurfum heldur ekki að hafa áhyggjur af því að afleiðan skipti um formerki á milli núllstöðva.

Sýnidæmi 1

Finnum afleiðu f(x) = x², gerum formerkjakönnun á henni og berum niðurstöðuna saman við grafið.

   Ef f(x) = x² þá er f´(x) = 2x.

Gerum nú formerkjakönnun á f´(x) = 2x og teiknum síðan grafið undir.

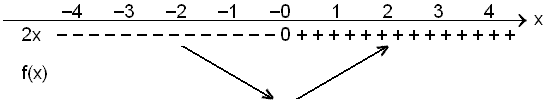
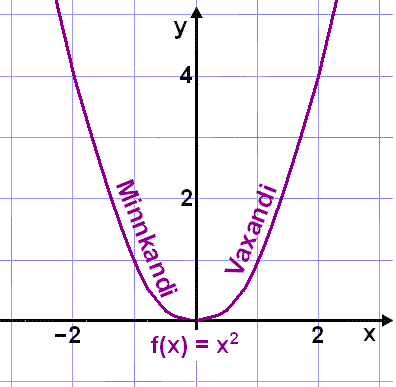
Botnpunkturinn er í x = 0 þar sem afleiðan er 0.

Sýnidæmi 2

Finnum afleiðu f(x) = x³ – 3x² + 4 gerum formerkjakönnun á henni og reiknum út staðbundin hágildi og lággildi. Berum niðurstöðuna síðan saman við graf úr grafískri reiknivél.

   Ef f(x) = x³ – 3x² + 4 þá er f´(x) = 3x² – 6x.

Finnum nú hvar afleiðan er 0.

    3x² – 6x = 0

   3x(x – 2) = 0

Þessi jafna hefur lausnir í x = 0 og x = 2 og afleiðan skiptir þar um formerki. Notum þetta til þess að gera formerkjakönnun á afleiðunni f´(x) = 3x² – 6x.

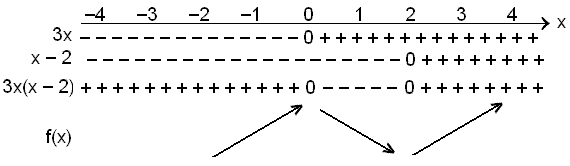
Við getum einnig gert formerkjakönnun án þess að þátta. Þá reiknum við út gildi á milli núllstöðvanna og sitt hvoru megin þeirra og setjum inn formerkin út frá því.

   f´(–1) = 3(–1)² – 6(–1) = 3 + 6 = 9    (+)

   f´(1) = 3·1² – 6·1 = –3                       (–)

   f´(3) = 3·3² – 6·3 = 9                         (+)

Þetta setjum við beint inn í formerkjakönnunina og fáum að sjálf sögðu sömu niðurstöðu.

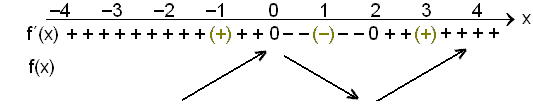
Við sjáum af formerkjakönnuninni að í x = 0 hlýtur að vera staðbundið hágildi vegna þess að grafið er þar lárétt í einum punkti (þar er afleiðan 0). Auk þess skiptir afleiðan um formerki úr + yfir í – sem merkir að grafið fer upp og síðan niður. Í x = 2 er afleiðan einnig 0. Þar skiptir afleiðan hins vegar um formerki úr – (niðurleið) yfir í + (uppleið) þannig að þar hlýtur að vera staðbundið lággildi. Reiknum nú út þessi gildi.

   f(0) = 0³ – 3·0² + 4 = 4

Staðbundið hágildi er í punktinum (0, 4).

   f(2) = 2³ – 3·2² + 4 = 8 – 12 + 4 = 0

Staðbundið lágildi er í (2, 0).

Grafið lítur svona út í grafískri reiknivél.

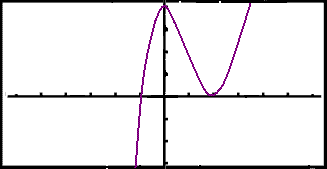Stundum verður afleiða falla 0 án þess að skipta um formerki. Í slíkum tilfellum fáum við ekki staðbundin hágildi eða lággildi. Grafið er hins vegar lárétt í þessum eina punkti og heldur síðan áfram að vaxa eða minnka eftir atvikum. Punktar af þessu tagi nefnast sætispunktar.

Sýnidæmi 3

Könnum fallið f(x) = x³.

Afleiðan er f´(x) = 3x² og núllstöð afleiðunnar er x = 0.

Gerum nú formerkjakönnun fyrir afleiðuna.

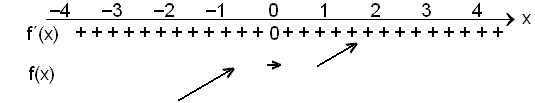
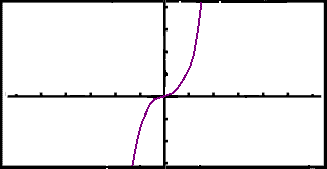
Punkturinn (0, 0) er sætispunktur vegna þess að fallið er á uppleið neðan við x = 0, flatt í x = 0 og heldur síðan áfram upp.

Útreikningar þar sem núllstöðvar afleiðu koma við sögu eru nýttir í margvíslegum hagnýtum tilgangi, einkum til þess að finna hágildi eða lágildi falla sem lýsa einhverju tilteknu vandamáli. Skoðum að lokum tvö sýnidæmi af þessu tagi.

Sýnidæmi 4

Pappaaskja er gerð úr spjaldi sem er 1 m á kant þannig að klippt er úr hornunum og brúnirnar brotnar upp (sjá mynd).

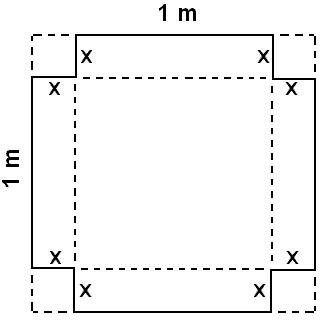
Hve mikið þarf klippa úr hornunum til þess að fá öskju með sem mestu rúmmáli?

Ef við klippum x m langan bút úr hverju horni verður askjan 2x styttri en spjaldið eða 1 – 2x á hvern kant. Hæð öskjunnar verður x þannig að rúmmálið R verður eftirfarandi:

   R = hæð·lengd·breidd

       = x(1– 2x)(1 – 2x)

       = x(1 – 4x + 4x²)

       = x – 4x² + 4x³

Finnum nú afleiðuna og síðan núllstöð hennar.

   R´ = 1 – 8x + 12x² = 0

Við verðum að nota lausnarformúlu annarrs stigs jöfnu eða grafíska reiknivél til þess að leysa þetta.

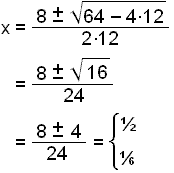
Ljóst er að lausnin getur ekki verið x = ½, en ef við klippum hálfan metra af hverju horni þá verður ekkert eftir þannig að lágmarkið er í x = ½. Hámarkið hlýtur þá að vera í x = .

   R() = (1 – 2·)(1 – 2·) = m³

Mesta rúmmál öskjunnar er m³ sem fæst með því að klippa bút sem er m á kannt úr hverju horni.

Sýnidæmi 5

Rétthyrningur hefur eina hlið á y-ásnum og aðra hlið á línunni y = 3. Rétthyrningurinn hefur hornpunktinn P á grafinu f(x) = x² (sjá mynd).

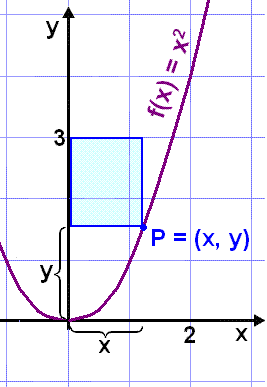
Lengd rétthyrningsins er x og hæðin 3 – y eða 3 – x² vegna þess að hornpunkturinn P er á grafinu f(x) = x². Finnum flatarmálið út frá þessu.

   F = lengd·hæð

      = x·(3 – x²) = 3x – x³

Finnum nú afleiðuna og núllstöðvar hennar.

   F´ = 3 – 3x² = 0

     3 = 3x²

     x = ±1

Nú er ljóst að rétthyrningurinn nær ekki yfir á neikvæðu hlið hnitakerfisins þannig að gildið x = –1 kemur ekki til greina. Hámarksflatarmálið kemur því fram í x = 1 sem gefur okkur óþekktu stærðina í formúlunni.

   F = 3x – x³ = 3 – 1 = 2

Æfðu þig á þessum aðferðum og taktu síðan próf 4 í Föllum 2.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum