© 2008  Rasmus ehf    og Jóhann Ísak

Föll 2

Kynning 6

Andhverf föll

Við höfum nú þegar kynnst nokkrum föllum sem eru andhverfur hvors annarrs. Þannig eru föllin f(x) = x² og g(x) = √x andhverf föll. Þessi föll upphefja hvort annað ef við vinnum aðeins með jákvæðar tölur. Skoðum eftirfarandi:

   f(x) = x² og g(x) =

   f(2) = 2² = 4 og g(4) = √4 = 2

   f(g(a)) = = a

   g(f(a)) =  = a

Ef við reiknum út gildi fyrir tiltekna tölu og setjum útkomuna inn í andhverfuna fáum við út sömu töluna aftur. Þetta gildir hvort sem f(x) eða g(x) er notað á undan. Varpmengi f(x) verður formengi g(x) og síðan verður varpmengi g(x) formengi f(x).

Taktu eftir því að við verðum að takmarka F_f við jákvæðar tölur. Það er vegna þess að fall hefur aðeins andhverfu ef það er gagntækt sem hefur í för með sér að það verður annað hvort að vera stöðugt vaxandi eða stöðugt minnkandi í formengi sínu. Þannig er fallið f(x) = x² stöðugt vaxandi ef formengið er aðeins jákvæðar tölur. Og fallið hefur andhverfuna g(x) = √x sem aðeins gengur á jákvæðar tölur.

Við getum fundið andhverfur falla með aðferðum jöfnureiknings og algebru. Aðferðin er fólgin í því að setja upp jöfnuna y = f(x) og leysa hana m.t.t. x. Skoðum dæmi um það.

Sýnidæmi 1

Finnum andhverfur nokkurra falla.

a)   f(x) = 2x + 4

          y = 2x + 4

      –2x = 4 – y

          x = –2 + ½y              Hér deilum við í gegn með –½.

      Nú höfum við fengið fall með breytunni y en hér skiptir ekki máli hvað breytan heitir við getum allt eins kallað hana x.
Við getum því sagt að g(x) = ½x – 2.

       Við getum nú prófað þessa niðurstöðu með tölu

          f(1) = 2·1 + 4 = 6 og g(6) = ½·6 – 2 = 3 – 2 = 1

      eða með almennri breytu

         f(a) = 2a + 4 = 6 og g(2a+4) = ½·(2a+4) – 2 = a + 2 – 2 = a

b)   f(x) = sin 2x,  F_f = [–p/4,p/4ñ

          y = sin 2x

        2x = sin^–1 y

          x = ½ sin^–1 y

      Andhverfan er fallið g(x) = ½ sin^–1 x. Taktu eftir að á reiknivélum og í mörgum bókum er andhverfan táknuð með veldisvísinum ^–1 á heiti eða bókstafi fallsins. Þessu má ekki rugla saman við einn á móti fallinu eins og neikvætt veldi á algebrustæðum og tölum merkir. Við hefðum því eins getað skrifað andhverfu f(x) = sem f ^–1(x) = ½ sin^–1 x.

      Prófun.

         f(p/12) = sin 2p/12 = ½ 

         f ^–1(½) = ½·sin^–1 ½ = ½·p/6 = p/12

c)   f(x) = e^2x

          y = e^2x

      ln y = ln e^2x = 2x

          x = ½ ln y

      Andhverfa f(x) er f ^–1(x) = ½ ln x.

d)   f(x) = x² – 1, F_f = R₊

          y = x² – 1

          x² = y + 1

        Andhverfan er

e)

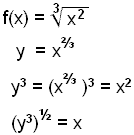Hér hefjum við báðar hliðar í þriðja veldi og síðan í hálfta veldi.

        Andhverfan er

Sýnidæmi 2

Hvernig þurfum við að takmarka formengi fallsins f(x) = sin x til þess að það geti haft andhverfu?

Þetta getum við séð bæði með því að skoða graf f(x) = sin x og afleiðuna f´(x) = cos x.

Gerum formerkjakönnun fyrir afleiðuna f´x) = cos x og notum einingarhringinn til viðmiðunar.

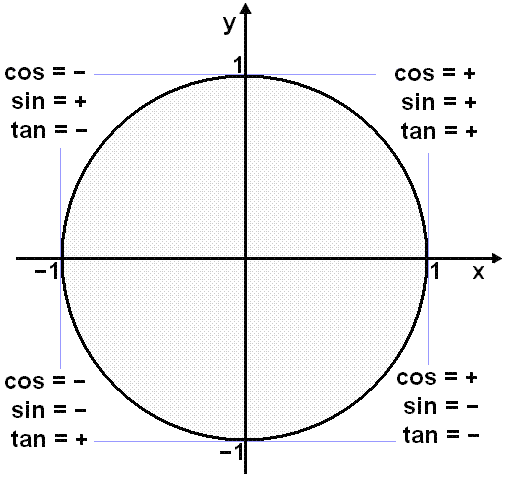
Við sjáum af einingarhringnum að cos x er jákvæður frá –p/2 (stefnan beint niður) upp í p/2 (stefnan beint upp) og neikvæð hinn hlutan af hringnum.

Skoðum einnig graf f(x) = sin x.

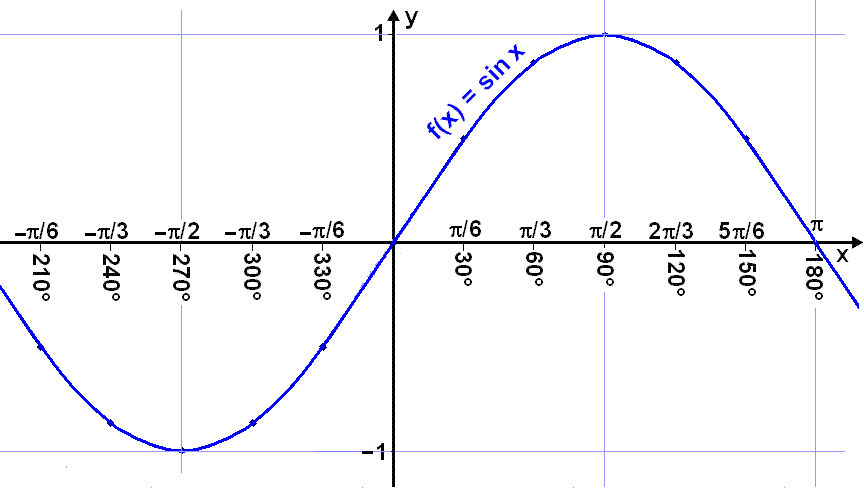
       Grafið er greinilega vaxandi á bilinu frá –p/2 < x < p/2 og fallið f(x) = sin x getur haft andhverfu á því bili.
 Við getum einnig valið eitthvað annað bil t.d. bilið p/2 < x < 3p/2 en á því bili er fallið stöðugt minnkandi.

Sýnidæmi 3

Finnum á hvaða bili fallið f(x) = x² – 4x + 3 er vaxandi, takmörkum formengið miðað við það og finnum síðan andhverfuna. Teiknum loks gröf f(x) og f^–1(x) í sama hnitakerfi.

Finnum fyrst botnpunkt fleygbogans og nú notum við afleiðuna og finnum núllstöð hennar.

   f(x) = x² – 4x + 3

   f´(x) = 2x – 4 = 0

      2x = 4

        x = 2

Botnpunkturinn er í x = 2 og fallið hlýtur að vera vaxandi þaðan. Við getum því valið formengið F_f = [2,®ñ.

Finnum nú andhverfuna með því að leysa jöfnuna y = x² – 4x + 3 m.t.t. x.

Þá er bara eftir að teikna gröfin. Byrjum á að reikna út nokkra punkta og setja í gildistöflu.

Við reiknum f(2) og sjáum að varpmengi f(x) verður frá y = –1 og upp. Þá sjáum viða að við þurfum að byrja að reikna út gildi fyrir f^–1(–1) vegna þess að varpmengi f(x) verður formengi f^–1(x).

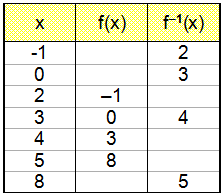
Gröfin líta svona út.

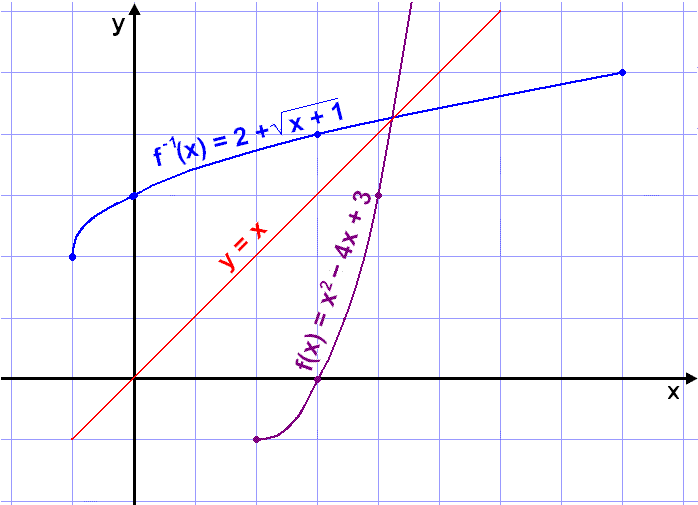
Taktu eftir því að gröfin eru spegilmyndir hvors annarrs (eða samhverf) um línuna y = x (sem er helmingalína hornsins á milli ásanna). Gildistaflan sýnir einnig að hnitapör koma fyrir í öfugri röð. Þannig eru t.d. punktarnir (2, –1) og (3, 0) á grafi f(x) en (–1, 2) og (0, 3) á grafi f ^–1(x). Almennt gildir að punkturinn (a, b) á grafi falls hefur samsvarandi punkt (b, a) á grafi andhverfunnar og það gildir um alla punkta sem eru samhverfir um línuna y = x.

Sýnidæmi 4

Skoðum fallið f(x) = e^x og andhverfu þess g(x) = ln x.

Fallið f(x) = e^x getur hvorki gefið neikvæða útkomu né útkomuna 0 þannig að varpmengi þess eru allar tölur ofan við 0.
Formengi g(x) = ln x er því einnig allar tölur ofan við 0 (bilið á0, ®ñ).
Varpmengi g(x) = ln x er hins vegar allar tölur enda verður það formengi f(x) = e^x.

Gröfin eru spegilmyndir hvors annarrs um línuna y = x eins og sést á grafinu hér fyrir neðan.

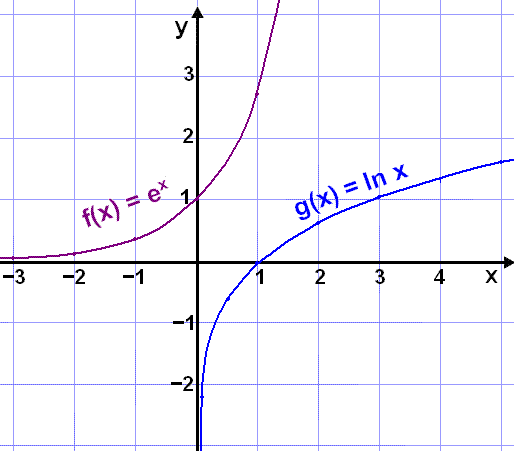
Sýnidæmi 5

Finnum á hvaða bili fallið er vaxandi. Veljum formengið út frá því og finnum andhverfuna.
Teiknum loks gröf fallsins og andhverfunnar í sama hnitakerfi.

Finnum fyrst afleiðuna og gerum formerkjakönnun.

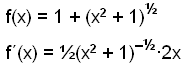
Ljóst er að nefnarinn er jákvæður fyrir öll x þannig að teljarinn x ræður formerki afleiðunnar og fallið er því vaxandi fyrir jákvæð x.

Við veljum því formengið F_f = [0, ®ñ.

Næst finnum við andhverfuna.

             y = 1 + (x² + 1)^½

       y – 1 = (x² + 1)^½

   (y – 1)² = x² + 1

            x² = (y – 1)² – 1

                = y² – 2y + 1 – 1

                = y² – 2y

Andhverfan er

Gröf f(x), f ^–1(x) og línunnar y = x líta svona út.

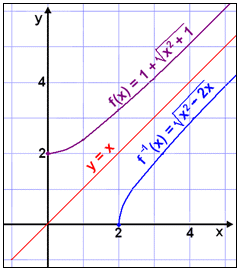
Sýnidæmi 6

Finnum andhverfu fallsins og skoðum graf þess og andhverfunnar í sama hnitakerfi.

Fallið hefur lóðfellu í x = 1 og láfellu í y = 2. Formengið getur því ekki innihaldið x = 1 og varpmengið ekki y = 2. Formengi andhverfunnar getur þá væntanlega ekki innihaldið x = 2.

Finnum afleiðuna og skoðum halla fallsins.

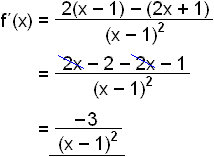
Nefnari þessa brots er alltaf jákvæður þannig að teljarinn ræður því að afleiðan er neikvæð fyrir öll x í formenginu. Fallið er því minnkandi í öllu formenginu (stöðugt á niðurleið) og hefur andhverfu.

Finnum nú andhverfuna.  

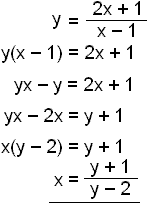
Andhverfan  er

Hér komum við breytunni x fyrst undan strikinu og færum það síðan á vinstri hlið. Þar er hægt að einangra það með því að færa allt annað yfir á hægri hlið.

Þetta fall hefur lóðfellu í x = 2 og lágfellu í y = 1. Þetta er þver öfugt við f(x) sem hafði lóðfellu í x = 1 og láfellu í y = 2 þannig að aðfellurnar speglast í línunni y = x líkt og gröfin. Við þurfum þess vegna ekki að hafa áhyggur af deilingu með núlli ef við gerum ráðstafanir í byrjum sem í þessu tilfelli fólst í því að taka x = 1 út úr formenginu.

Skoðum nú gröf fallanna.

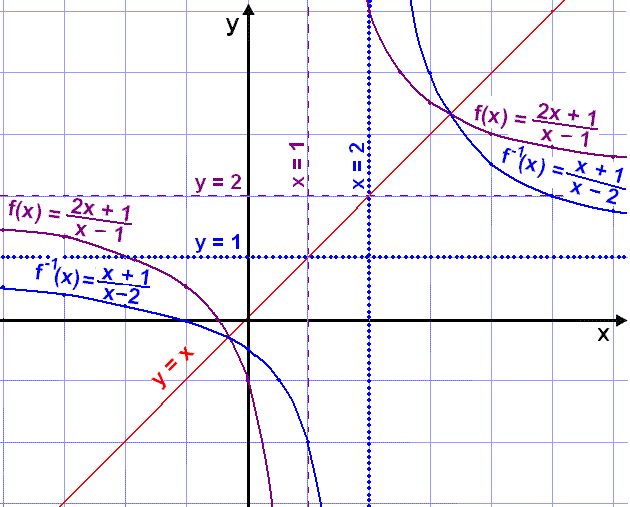
Bæði aðfellurnar og gröfin eru samhverf um línuna y = x.

Æfðu þig á þessum aðferðum og taktu síðan próf 6 í Föllum 2.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum