© 2007 Rasmus ehf og Jóhann Ísak Pétursson
© 2007 Rasmus ehf og Jóhann Ísak Pétursson |
Mengi kynning 2 |
|
Nokkur talnamengi eru notuğ í stærğfræğinni. Sameiginlegt einkenni şeirra er óendanlegur fjöldi staka. Eftirfarandi mynd sınir şrjú şessara mengja.
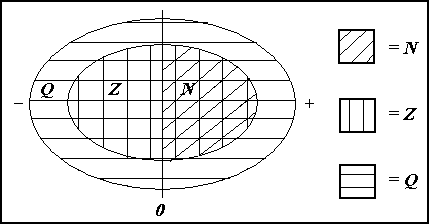
Einfaldasta mengiğ er mengi náttúrulegra talna, mengiğ N = {1,2,3,∙∙∙}. Şetta eru tölurnar sem viğ notum til şess ağ telja meğ heila hluti og şağ er engin fræğileg takmörk á şví hve hátt er hægt ağ telja. Núlliğ er algeng viğbót viğ şetta mengi og şá er komiğ mengiğ N0 = {0,1,2,3,∙∙∙} sem oft er notağ í fræğunum.
Mengiğ Z, mengi heilla talna, er talsvert yfirgripsmeira. Şağ nær yfir 0 og allar náttúrulegar tölur og şar ağ auki allar neikvæğar heilar tölur. Şetta má tákna Z = {∙∙−2,−1,0,1,2,∙∙}. Mengiğ N er şví eiginlegt hlutmengi í Z.
N
![]() Z
Z
Enn yfirgripsmeira er mengi ræğra talna, mengiğ Q. Şağ er mengi allra şeirra talna sem hægt er ağ tjá nákvæmlega meğ tölustöfum, annağ hvort meğ heilum tölum eğa almennum brotum, jákvæğum eğa neikvæğum. Mengin Z og N eru eiginleg hlutmengi í Q.
Z
![]() Q og N
Q og N
![]() Q
Q
Taktu eftir şví ağ tugabrot eru ekki nefnd í şessu samhengi, enda eru şau talsvert takmarkağri en almenn brot. Einfalda ræğa tölu eins og t.d. 1/3 er ekki hægt ağ tjá meğ endanlegu tugabroti.
 Sınidæmi 1
Sınidæmi 1og |
Reiknum í vasareikni 1 deilt meğ 3
![]()
sem gefur 0,333∙∙∙∙
og 4 deilt meğ 33
![]()
sem gefur 0,1212∙∙∙∙
Óendanlegu tugabrotin í sınidæminu hér fyrir ofan eru kölluğ lotubundin tugabrot vegna şess ağ sömu tölurnar endurtaka sig endalaust. Í fyrra dæminu er lotan einn tölustafur (3 endurtekur sig) og í şví síğara er lotan tveir tölustafir (1 og 2 endurtaka sig). Meğ lotubundnum tugabrotum má tjá allar ræğar tölur og şar meğ öll almenn brot.
Viğ höfum nú skoğağ hvernig breyta má almennu broti í tugabrot (teljari deilt meğ nefnara). Nú skulum viğ athuga hvernig breyta má tugabroti til baka í almennt brot.
Ef tugabrotiğ er endanlegt şá breytum viğ şví sem er aftan viğ kommu í tíundu hluta, hundruğustu hluta, şúsundustu hluta o.s.frv. allt eftir şví hve margir aukastafirnir eru hverju sinni.
Breytum 0,3, 0,12 og 0,1212 í almenn brot.
0,3 |
= |
|
= |
|
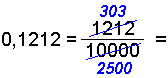 |
Şetta verğur dálítiğ flóknara ef tugabrotiğ er lotubundiğ. Şá şurfum viğ ağ beita frádrætti meğ dálítilli útsjónasemi til şess ağ eyğa lotunni.
Breytum 0,333∙∙∙∙∙, 0,1212∙∙∙∙∙ og 1,14333∙∙∙∙ í almenn brot.
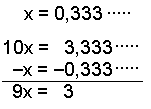 |
Viğ drögum töluna frá tífaldri tölunni, en viğ şağ dettur lotan út. |
|
|
Ağ lokum er deilt í gegn og stytt. |
|
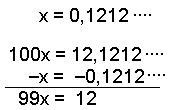 |
Hér şurfum viğ ağ draga töluna frá hundrağfaldri tölunni til şess ağ lotan detti út. |
|
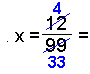 |
||
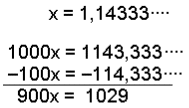 |
Hér şurfum viğ ağ draga hundrağfalda töluna frá şúsundfaldri tölunni til şess ağ lotan detti út. |
|
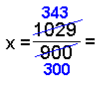 |
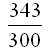 |
|
Æfğu şig á şessum ağferğum og taktu síğan próf
2 í Mengjum.
ps. mundu eftir ağ fylla út í tékklistann şinn jafnóğum