© 2007  Rasmus ehf    og Jóhann Ísak Pétursson

Þáttun margliðu

Kynning 1     Margliðudeiling og leifareglan

Skoðum margliðuna f(x) = 6x² − 9x + 3 og gerum ráð fyrir að við höfum fundið út fyrir tilviljun t.d. við gerð gildistöflu, að f(1) = 0. Það að f(1) er jafnt og 0 sýnir okkur að (x − 1) er þáttur í f(x).

Ef x er 1 þá er (x − 1) = 0, en það gerir alla stæðuna að núlli.

    f(x) = 6x² − 9x + 3 = (óþekktur svigi)(x − 1)

    f(1) = 6 − 9 + 3 = (óþekktur svigi)(1 − 1) = (óþekktur svigi)∙0

           = 0

Nú er deiling andhverfa margföldunar þannig að við getum deilt 6x² − 9x + 3 með x − 1 og fengið þannig út óþekkta svigann. Við skulum nú skoða hvernig þetta er gert og bera það saman við venjulega talnadeilingu.

Sýnidæmi 1

Talnadeiling:

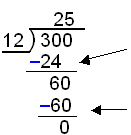Hve oft ganga 12 upp í 30? 2 sinnum. 2∙12 = 24. Drögum 24 frá 30 og tökum niður 0. Hve oft ganga 12 upp í 60. 5 sinnum. 5∙12 = 60. Drögum 60 frá.

Algebrudeiling:

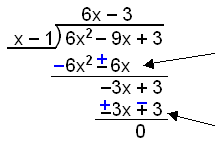Hve oft ganga x − 1 upp í 6x2? 6x sinnum. 6x∙(x − 1) = 6x2 − 6x. Drögum 6x2 − 6x frá með því að breyta formerkjum. Tökum niður +3.   Hve oft ganga x − 1 upp í −3x? −3 sinnum. −3∙(x − 1) = −3x + 3. Drögum −3x + 3 frá með því að breyta formerkjum.

f(x) = 6x² − 9x + 3 má samkvæmt þessu þátta í (6x − 3)(x − 1).

Sýnidæmi 2

Við getum einnig notað lausnarformúluna til þess að þátta stæðuna 6x² − 9x + 3.

Við byrjum á því að leysa jöfnuna 6x² − 9x + 3 = 0. Stuðlarnir eru a = 6, b = −9 og c = 3.

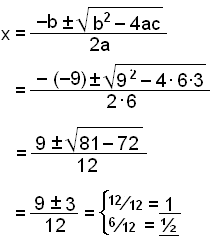
Lausnirnar á jöfnunni eru 1 og ½ þannig að svigarnir (x − 1) og (x − ½) hljóta báðir að vera þættir í

6x² − 9x + 3. Niðurstaðan er þá eftirfarandi:

    6x² − 9x + 3 = 6(x − 1)(x − ½).

Þetta má síðan prófa með margföldun.

Af dæminu hér á undan sjáum við að annars stigs margliðu má umrita (þátta) á eftirfarandi hátt:

ax² + bx + c = a(x − r₁)(x − r₂)

Margliðan verður þá að hafa tvær lausnir r₁ og r₂.

Sýnidæmi 3

Við skulum nú deila margliðunni x³ − 6x² + 11x − 6 með x − 1 og fullþátta hana síðan.

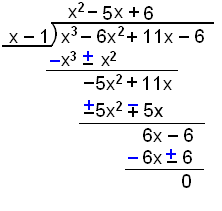	x gengur x2 sinnum upp í x3. x2(x − 1) = x3 − x2. Drögum x3 − x2 frá með því að breyta formerkjum.
	x gengur −5x sinnum upp í −5x2. −5x(x − 1) = −5x2 + 5x. Drögum −5x2 + 5x frá með því að breyta formerkjum.
	x gengur 6 sinnum upp í 6x. 6(x − 1) = 6x − 6. Drögum 6x − 6 frá með því að breyta formerkjum.

Útkoman er annars stigs margliða og hana getum við þáttað með ágiskun eða lausnarformúlunni. Niðurstaðan er eftirfarandi:

x³ − 6x² + 11x − 6 = (x² − 5x + 6)(x − 1) = (x − 3)(x − 2)(x − 1)

Sýnidæmi 4

Við skulum líta á svolítið snúnara dæmi.

Deilum margliðunni x³ − 4x + 3 með x − 1 og fullþáttum hana síðan.

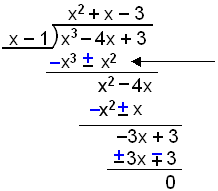Hér megum við ekki blanda saman x2 og −4x. Báðir liðirnir koma því óbreyttir niður.

Nú eigum við eftir að þátta x² + x − 3. Það gengur varla með ágiskun þannig að við verðum að nota lausnarformúluna.

Hér er a = 1, b = 1 og c = −3.

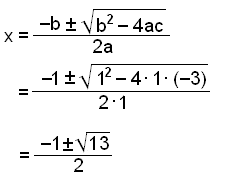
Þáttunin verður því eftirfarandi:

x³ − 4x + 3 = (x² + x − 3)(x − 1)

Sýnidæmi 5

Við skulum nú skoða deilingardæmi sem gengur ekki upp. Deilum x³ + 4x² + x + 1 með x + 1.

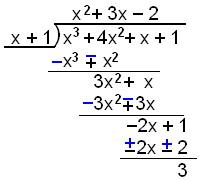
Afgangurinn eða leifin eins og þetta kallast er 3 í þessu dæmi.

Við getum hins vegar umritað margliðuna á eftirfarandi hátt:

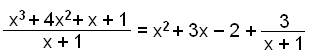
Þessi umritun verður mikilvæg í framhaldinu:

Samkvæmt sýnidæminu hér fyrir ofan þá gefur margliðudeiling okkur eftirfarandi jöfnu:

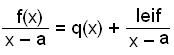
Ef við margföldum í gegnum jöfnuna með x − a þá fáum við eftirfarandi umritun á margliðunni f(x):

    f(x) = q(x)(x − a) + leif

Notum nú þessa umritun til þess að reikna f(a).

    f(a) = q(a)(a − a) + leif

    f(a) = q(x)∙0 + leif

    f(a) = leif

Þetta sýnir okkur að við þurfum ekki að deila til þess að finna út hvað verður afgangs í margliðudeilingu.

Við höfum leitt út reglu sem nefnist leifareglan og er eftirfarandi:

    Ef margliðunni f(x) er deilt með x − a þá verður leifin eða

    afgangurinn f(a).

Sýnidæmi 6

Við skulum nú nota leifaregluna til þess að finna hvað verður afgangs þegar x³ + 4x² + x + 1 er deilt með x + 1.

Nú gildir leifareglan fyrir deilingu með x − a eða a með breyttu formerki. Ef við ætlum að nota hana fyrir deilingu með x + 1 þá verðum við að finna f(−1).

    f(−1) = (−1)³ + 4∙(−1)² + (−1) + 1

            = −1 + 4 − 1 + 1

            = 3

Þetta passar við niðurstöðuna úr sýnidæmi 5.

Sýnidæmi 7

Við skulum að lokum nota leifaregluna til þess að finna hvað verður afgangs þegar x³ + 4x² + x + 1 er deilt með x − 1.

Leifareglan gildir fyrir deilingu með x − a (eða a með breyttu formerki) og því gefur f(1) leifina beint þegar f(x) er deilt með    x − 1.

    f(1) = 1³ + 4∙1² + 1 + 1

          = 1 + 4 + 1 + 1

          = 7

Æfðu þig á þessum aðferðum og taktu síðan próf 1 í Þáttun margliða.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum