© 2007  Rasmus ehf    og Jóhann Ísak Pétursson

Veldareglur og lograr.

Kynning 2     Lograr með grunntöluna 10

Fátt er eins þægilegt í stærðfræði og að margfalda saman tölur á borð við 1, 10, 100, 1000 o.s.frv. Við þurfum aðeins að leggja saman fjölda núlla.

T.d. er 10∙100∙1000 = 1 000 000 enda eru núllin samtals 6.

Þetta kemur enn betur í ljós ef við reiknum með veldum.

10∙100∙1000 = 10¹∙10²∙10³ = 10¹⁺²⁺³ = 10⁶ = 1000000.

Fyrir um 400 árum datt mönnum í hug að breyta tölum í veldi af 10 til þess að geta margfaldað þær saman með samlagningu veldisvísa. Þeir fundu upp fallið f(x) = log x þar sem f(a) eða log a er veldisvísir sem setja má á grunntöluna 10 þannig að útkoman verði a. Fallið f(x) = log x finnur veldisvísa á 10 sem búa til allar jákvæðar tölur. Aðeins jákvæðar tölur vegna þess að veldisvísir getur aldrei búið til neikvæða útkomu eða núll úr jákvæðu grunntölunni 10.

Fallið f(x) = log x hefur því formengið F_f = { x R | x > 0 }.

Skoðum þetta fall og reiknum út nokkur gildi á reiknivélinni. Það er gert með tökkum merktum log eða log. Á reiknivélum af CASIO-gerð er aðgerðaröðin eftirfarandi:

f(1) = log 1 = 0 enda er 10⁰ = 1

f(2) = log 2 ≈ 0,303 enda er 10^0,303 ≈ 2

f(3) = log 3 ≈ 0,477 enda er 10^0,477 ≈ 3

f(10) = log 10 = 1 enda er 10¹ = 10

f(20) = log 20 ≈ 1,303 enda er 10^1,303 ≈ 20

f(100) = log 100 = 2 enda er 10² = 100

f(1000) = log 1000 = 3 enda er 10³ = 1000

Við sjáum að fallið f(x) = log x er í raun andhverfa fallsins g(x) = 10^x í þeim skilningi að föllin upphefja hvort annað líkt og kvaðratrót upphefur annað veldi.

Sýnidæmi 1

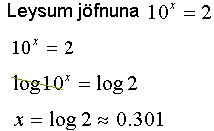Við tökum logra af báðum hliðum jöfnunnar. Föllin log x og 10 x upphefja hvort annað þannig að á vinstri hlið jöfnunnar stendur x eitt eftir

Sýnidæmi 2

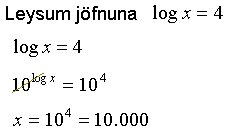Við setjum báðar hliðar jöfnunnar sem veldi á grunntöluna 10. Föllin log x og 10x upphefja hvort annað þannig að á vinstri hlið jöfnunnar stendur x eitt eftir.

Lograr eru í raun veldisvísar þannig að fyrir þá gilda reglur sem samsvara veldareglunum.

Ef t.d. x = log a og y = log b þá er 10^x∙10^y = 10^x+y og þar af leiðandi er log ab = log a + log b.

Á sama hátt má finna að log( ^a/_b)= log a − log b.

Við sjáum einnig að log aⁿ = log a + log a + ∙ ∙ ∙ ∙ + log a (n liðir) = n log a.

Við getum því notað eftirfarandi þrjár lograreglur:

Sýnidæmi 3

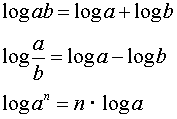
Notum lograreglurnar til þess að einfalda eftirfarandi stæður og skrifa þær sem einn logra:

a)  log a + log b + log c = log abc

b)  log a + log 2b + log 3c + log 4 = log a∙2b∙3c∙4 = log 24abc

c)  log a + log a + log a = 3 log a = log a³

d)  log 2a − log 2b = log 2 + log a − log 2 − log b = log ^a/_b

e)  ¼∙(log a + log a³) = ¼∙(log a + 3 log a) = ¼∙4 log a = log a

Sýnidæmi 4

Skrifum vinstri hliðar eftirfarandi jafna sem einn logra og leysum síðan jöfnurnar.

a) 

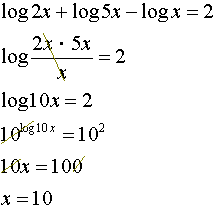Við byrjum á því að nota lograreglurnar til þess að skrifa vinstri hliðina sem margföldun og deilingu í stað samlagningar og frádráttar. Að lokum setjum við báðar hliðar sem veldi á 10 og deilum í gegn til þess að einangra x.

b)

c)

d)

Reglan  log aⁿ = n log a  er notuð til þess að leysa jöfnur af gerðinni a^x = b. Aðferðin byggist af á því að taka logra af báðum hliðum og nota síðan regluna til þess að koma óþekkta x-inu úr veldisvísinum.

    a^x = b

    log a^x = log b

    x log a = log b

    x = ^{log b}/_{log a}

Sýnidæmi 5 

Æfðu þig á þessum aðferðum og taktu síðan próf 2 í Veldi og lograr.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum