© 2007  Rasmus ehf    og Jóhann Ísak Pétursson

Veldareglur og lograr.

Kynning 3     Náttúrulegur logri

Í tímans rás hefur dregið úr gagnsemi logra með grunntölunni 10, sérstaklega eftir að öflugar reiknivélar og tölvur komu til sögunnar. Aftur á móti hefur svokallaður náttúrulegur logri reynst hafa vaxandi hagnýtt gildi í margvíslegum vísindum.

Náttúrulegur logri byggir á grunntölu sem nefnd hefur verið e. Hann hefur skammstöfunina ln og þannig er fallið merkt á reiknivélum.

Sýnidæmi 1

Notum CASIO-reiknivél til þess að finna náttúrulega logrann af 2. Aðgerðaröðin er eftirfarandi:

Útkoman verður um það bil 0,693 sem ætti að vera sá veldisvísir sem setja þarf á töluna e til þess að 2 komi út.

   e^0,693 ≈ 2

Prófum það á reiknivélinni:

Þetta gefur útkomuna 1,9997 ≈ 2.

Föllin f(x) = ln x og g(x) = e^x upphefja hvort annað líkt og ferningsrót upphefur annað veldi. Sagt er að f(x) = ln x er andhverfa eða andhverft fall við g(x) = e^x.

Eftirfarandi gildir:

    ln e^x = x og e^{ln x} = x

Talan e er óræð þannig að ekki er hægt að skrifa hana nákvæmlega, en við getum reiknað hana út með þeirri nákvæmni sem við viljum með því að setja stór gildi fyrir x inn í eftirfarandi formúlu.

Sýnidæmi 2

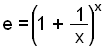
Prófum að reikna út e með því að setja x = 1000.

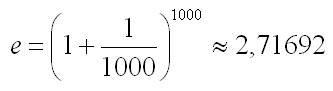
Samkvæmt töflureikninum EXCEL er rétt svar 2,7182818284591 þannig að við höfum aðeins fengið tvo rétta aukastafi.

Prófum nú að reikna þetta með x = 1000000.

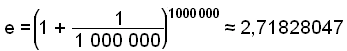
Hér höfum við fengið fimm rétta aukastafi, en ef við hins vegar gætum hækkað x upp í óendanlegt og hefðum nógu öfluga reiknivél þá fengjum við óendanlega marga rétta aukastafi.

Sýnidæmi 3

Skoðum nú gröf fallanna f(x) = ln x og g(x) = e^x.

Reiknum fyrst gildistöflur:

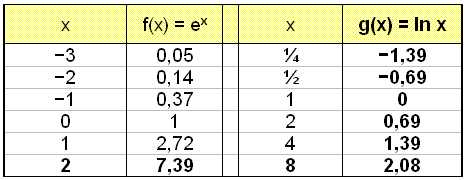
Taktu eftir því að fallið g(x) = e^x framleiðir engar neikvæðar tölur þannig að andhverfa fallið f(x) = ln x getur ekki tekið við neinum neikvæðum tölum.

Formengi f(x) = ln x er F_f = { xÎR | x > 0 }.

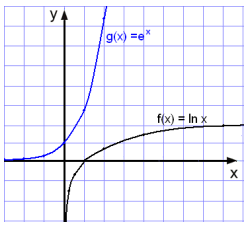
Taktu eftir því að gröfin mynda spegilmynd um hornalínu hnitakerfisins (línuna y = x), en það er eitt af einkennum andhverfra falla.

Sams konar reglur gilda fyrir náttúrulegan logra eins og fyrir logra með grunntöluna 10.

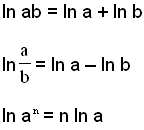
Við skulum nú skoða nokkur dæmi um það hvernig þessar reglur eru notaðar.

Sýnidæmi 4

Einföldum vinstri hlið eftirfarandi jafna og leysum síðan jöfnurnar.

a)

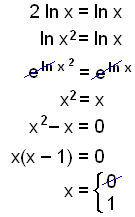Við byrjum á því að skrifa þetta sem einn logra og upphefja síðan logrann með því að setja báðar hliðar sem veldisvísi á e. Hér er komin annars stigs jafna.

   Taktu eftir því að svarið x = 0 er ekki gilt vegna  þess að e^x getur aldrei orðið 0.

b)

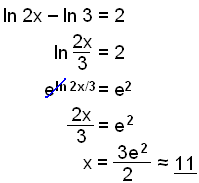Skrifum sem einn logra. Setjum sem veldi á e.

c)

Skrifum sem einn logra.
Einföldum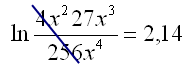
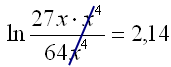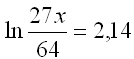Setjum sem veldi á e.

Sýnidæmi 5 

Leysum eftirfarandi jöfnur:

a)

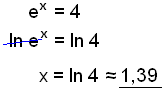Tökum logra af báðum hliðum

b)

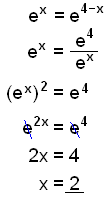Hér notum við veldaregluna a x− y = ax/ay. Hér notum við veldaregluna (a n)m = a nm.

c)

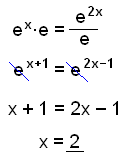Hér notum við veldareglurnar a x∙a y = a x+y og a x/a y = a x−y til þess að fá eina veldastærð á hvora hlið.

Sýnidæmi 6

Leysum eftirfarandi jöfnur:

a)

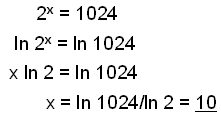Við tökum logra sitt hvoru megin og notum síðan logra-regluna ln a x= x ln a til þess að færa óþekkta veldisvísinn framfyrir.

b)

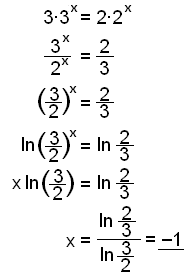Við sameinum x-in á vinstri hlið og einföldum með veldareglu. Síðan tökum við logra af báðum hliðum og einangrum x.

c)

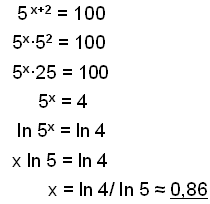Við einföldum fyrst og tökum síðan logra sitt hvoru megin.

Æfðu þig á þessum aðferðum og taktu síðan próf 3 í kaflanum um veldi og logra.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum