© 2007 Rasmus ehf og Jóhann Ísak Pétursson
© 2007 Rasmus ehf og Jóhann Ísak Pétursson |
Rætur og veldi |
|
Við skulum nú líta á tengsl velda og róta.
Við vitum að 2∙2 = 22= 4 |
þannig að Ö4 = 2. |
Einnig er 2∙2∙2 = 23 = 8 |
þannig að 3Ö8 = 2. |
Þrír eru hér svokallaður rótarvísir |
Taktu eftir því að við ferningsrót er hefð fyrir því að skrifa ekki rótarvísi, en þar ætti raunar að standa 2 vegna þess að ferningsrót er önnur rót.
Skoðum eftirfarandi ( a er jákvæð tala ) :
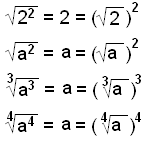
o.s.frv.
Veldi og rætur upphefja hvort annað líkt og margföldun upphefur deilingu. Jafnan (a2)x = a hefur aðeins lausnina ½ þannig að ferningsrót hlýtur að vera sama og veldið hálfur.
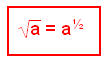 |
Ferningsrótin er sama og veldið hálfur |
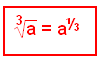 |
Þriðjarótin er sama og veldið einn þriðji Þetta gildir einnig fyrir þriðju rótina |
Einföldum eftirfarandi stæður þannig að þær verði a í einhverju einu veldi:
a)
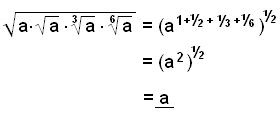 |
Við byrjum á því leggja saman alla veldisvísa undir fernings-rótinni og marg-földum síðan með hálfum. |
b)
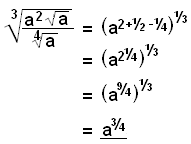
Þegar við þurfum að leysa jöfnu af gerðinni
![]()
hefjum við báðar hliðar í veldið b/a.
Leysum eftirfarandi jöfnur:
a)
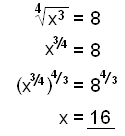 |
|
b)
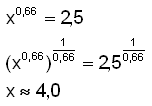 |
|
|
veldið |
||
Það virðist einfalt að
eyða rótum og brotnum veldum úr jöfnum með því að hefja báðar hliðar
í gagnstætt veldi. En við getum ekki alltaf gert það hugsunarlaust.
Jafntöluveldi (2, 4, 6, o.s.frv.) eyða neikvæðum stærðum úr jöfnunni þannig
að við getum fengið röng svör. Í slíkum tilvikum þurfum við að prófa
svörin.
Skoðum eftirfarandi jöfnu:
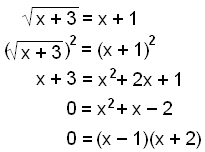
Þetta gefur okkur lausnirnar x = 1 og x = −2. Við skulum prófa þær.
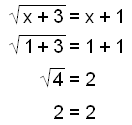
Lausnin x = 1 er í lagi.
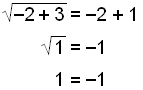
Lausnin x = −2 gengur ekki. Við höfum eytt mínus á hægri hlið jöfnunnar með því að hefja hana í annað veldi.
Við getum einnig fengið tvær gildar lausnir á svona jöfnum. Skoðum það.
Lítum á eftirfarandi jöfnu:
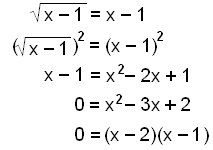
Þetta gefur lausnirnar x = 1 og x = 2. Prófum þær.
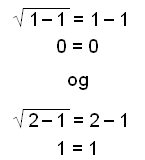
Báðar lausnirnar eru
gildar.
Æfðu þig á þessum aðferðum og taktu síðan próf
2 í rótum.
ps. mundu eftir að fylla út í tékklistann þinn jafnóðum