Rasmus.is - Jöfnur III

Jöfnur III

Kynning 1 Annars stigs jöfnur

Við skulum nú skoða lausnir á annars stigs jöfnum. Það jafngildir því að finna hvar gröf falla á borð við f(x) = ax² + bx + c skera x-ás hnitakerfisins.

Skoðum fyrst þau tilfelli þar sem annan hvorn seinni liðanna vantar (b = 0 eða c = 0).

Sýnidæmi 1

a) 2x² − 8 = 0
          2x² = 8
            x² = 4
             x = ±2

Fyrst einangrum við x²og síðan er dregin ferningsrót af báðum hliðum jöfnunnar og gert ráð fyrir + og − svari.

b) 2x² + 8 = 0
           2x² = −8
             x² = −4
   engin lausn

Hér gengur ekki að draga ferningsrót hægra megin vegna þess að þar er neikvæð tala.

Sýnidæmi 2

a)   2x² − 8x = 0
      2x(x − 4) = 0
      2x = 0 eða x − 4 = 0
        x = 0 eða x = 4

Hér getum við þáttað með því að taka 2x út fyrir sviga. Annar hvor þátturinn hlýtur að vera 0 vegna þess að margfeldi þeirra er 0.

b)   2x² + 8x = 0
      2x(x + 4) = 0
      2x = 0 eða x + 4 = 0
      x = 0 eða x = −4

Hér fáum við einnig tvær lausnir. Þessi gerð af jöfnum (þegar c = 0) hefur það alltaf.

Ef stuðlarnir a, b og c eru allir til staðar þá vandast málið. Þó ekki tiltakanlega ef jafnan passar við regluna

p² ± 2pq + p² = (p ± q)²

Sýnidæmi 3

a)    x² + 2x + 1 = 0
             (x + 1)² = 0
               (x + 1) = 0
                        x = −1

Þetta passar beint við í regluna.

b)    2x² − 8x + 8 = 0
      2(x² −4x + 4) = 0
             2(x – 2)² = 0
                 (x − 2) = 0
                          x = 2

Þegar búið er að taka 2 út fyrir sviga passar þetta við regluna.

Stundum er hægt að þátta stæðuna með ágiskun og finna síðan hvar sitt hvor liðurinn verður núlli.

Sýnidæmi 4

Leysum jöfnuna x² − 5x + 6 = 0

x² − 5x + 6 = 0

(x − 2)(x − 3) = 0

x = 2 eða x = 3

Sýnidæmi 5

Leysum jöfnuna x² − 4x − 5 = 0.

x² − 4x − 5 = 0

x² − 4x + 2² − 2² − 5 = 0

(x² − 4x + 4) − 9 = 0

Hér bætum við inn hálfum stuðlinum b í öðru veldi til þess að stæðan passi inn í regluna

p²± 2pq + q² = (p ± q)²

(x − 2)² − 9 = 0

Útkoman hér er lausnar-formið

x − 2 = ±3

x = 2 ± 3

x = 5 eða x = −1

(x + r)² + s sem sýnt var í kynningu 3 í föllum 1.

Sýnidæmi 6

Leysum jöfnuna 3x² − 24x + 21 = 0

3(x² − 8x) + 21 = 0

3(x² − 8x + 4²) − 3∙4² + 21 = 0

3(x − 4)² − 48 + 21 = 0

3(x − 4)² = 27

(x − 4)² = 9

x − 4 = ±3

x = 4 + 3 = 7 eða x = 4 − 3 = 1

Sýnidæmi 7

Búum nú til alhliða lausnarformúlu fyrir jöfnuna ax² + bx + c = 0 með því að nota algebru.

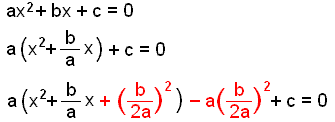	*Við byrjum á því að taka a út fyrir.* *Síðan bætum við inn hálfum stuðlinum við x í öðru veldi, en fyrir utan svigann þarf að margfalda stuðulinn með a.*
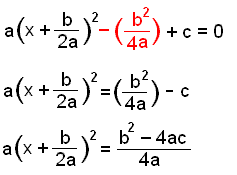	*Nú búum við til tvíliðastærð í öðru veldi samkvæmt reglunni.* *Allt annað færum við yfir jafnaðar-merkið og setjum upp á eitt strik.*

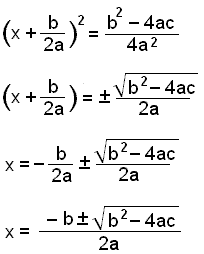Við losnum við annað veldi með því að draga ferningsrót af báðum hliðum.

Loks einangrum við x á vinstri hlið og setjum hægri hliðina upp á eitt strik.

Þetta er heilmikil flækja, en kosturinn við hana er sá að við þurfum ekki að leiða þett út nema einu sinni. Nú höfum við formúlu sem nota má á allar annars stigs jöfnur.

Lausnarformúla jöfnunnar ax² + bx + c = 0

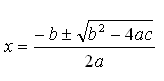Þessi jafna er mikið notuð og gengur undir ýmsum gælunöfnum svo sem „Jónas“, „hakkavélin“ o.fl.

Sýnidæmi 8

Við skulum nú nota þessa formúlu til þess að leysa jöfnuna

2x² − 10x + 8 = 0

Stuðlarnir eru eftirfarandi: a = 2

b = −10

c = 8

Setjum nú þessa stuðla inn í formúluna.

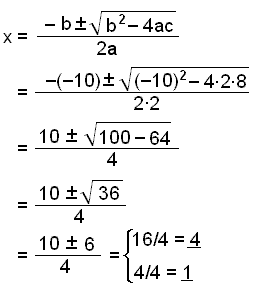
Sýnidæmi 9

Leysum jöfnuna x² − 3x + 6 = 0

Stuðlarnir eru a = 1, b = −3 og c = 6. Setjum þetta inn í jöfnuna.

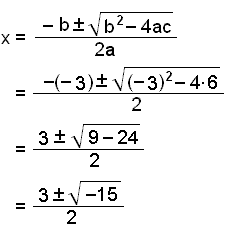
Þessir útreikningar enda með neikvæðri stærð undir ferningsrót þannig að jafnan hefur enga lausn.

Sýnidæmi 10

Við skulum nú leysa jöfnuna 2x² − 10x + 8 = 0 í grafískri CASIO-reiknivél.

Við byrjum á því að velja jöfnulausnir eða „EQUA“ á aðalvalmyndinni.

Þá fáum við eftirfarandi valmynd:

Nú veljum við „Polynomial“ (margliðu) með F2 og fáum upp eftirfarandi valmynd:

Hér fáum við lausnarform annars stigs margliðu með því að velja 2 með F1, en einnig má hér leysa þriðja stigs margliðu með því að velja hinn möguleikann. Nú fáum við upp eftirfarandi valmynd:

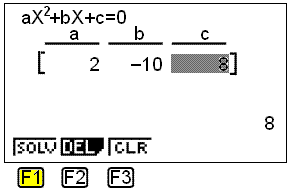
Hér setjum við inn stuðlana a = 2, b = −10 og c = 8. Aðgerðaröðin er eftirfarandi:

Að lokum veljum við SOLV (leysa) með F1. Lausnirnar 4 og 1 koma fram á eftirfarandi valmynd:

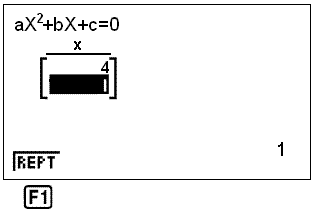
Sýnidæmi 11

Við skulum nú skoða hvað reiknivélin gerir við óleysanleg dæmi svo sem jöfnuna x² − 3x + 6 = 0. Við sláum inn stuðlana a = 1, b = −3 og c = 6. Vélin gefur eftirfarandi niðurstöður:

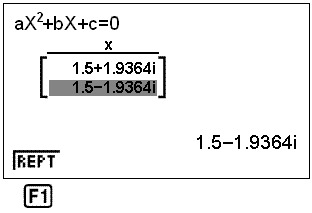
Þetta merkir að lausnin er svokölluð tvinntala sem tilheyrir ekki rauntölukerfinu. Engin rauntölulausn er til.

Sýnidæmi 12

Við skulum nú skoða hvernig leysa má annars stigs jöfnur í töflureikninum EXCEL. Við setjum upp eftirfarandi töflu:

Við skulum byrja á því að leysa jöfnuna 2x² − 10x + 8 = 0.

Við skrifum stuðlana a, b og c í reiti A3, B3 og C3.

Í reit B5 skrifum við formúluna

=B3^2-4*A3*C3.

Í reit B7 skrifum við formúluna

=IF(B5<0;"Engin lausn!";(-B3+SQRT(B5))/(2*A3))

Í reit B9 skrifum við loks formúluna

=IF(B5<0;"Engin lausn!";(-B3-SQRT(B5))/(2*A3))

Ef við notum þetta forrit til þess að leysa jöfnu sem hefur aðeins eitt svar eins og t.d. x² − 2x + 1 = 0 þá fáum við tvisvar sama svarið.

Ef dæmið er óleysanleg eins og t.d. jafnan x² − 3x + 6 = 0 þá verður niðurstaðan svona:

Æfðu þig á þessum aðferðum og taktu síðan próf 1 í Jöfnum 3.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum