© 2007  Rasmus ehf    og Jóhann Ísak Pétursson

Jöfnur III

Kynning 2    Þriðja stigs jöfnur og jöfnur af hærra stigi

Hvernig getum við fundið heiltölulausn jöfnu á borð við eftirfarandi þriðja stigs jöfnu?

    x³ − x² – 4x + 4 = 0

Til er flókin formúla til þess að leysa þriðja stigs jöfnur og góðar reiknivélar leysa þetta fyrir okkur. Við skulum hins vegar leysa þetta með þáttun. Ef jafnan hefur heiltölulausnirnar a, b og c þá má þátta hana á eftirfarandi hátt:

    x³ − x² – 4x + 4 = (x − a)(x − b)(x − c) = 0

Ef við margföldum svigana saman sjáum við að heiltöluliðurinn 4 hlýtur að vera margfeldi lausnanna a, b og c.

    abc = 4

Allar lausnirnar hljóta því að ganga upp í fjórum og það eru ekki svo margar heiltölur sem gera það. Möguleikarnir eru eftirfarandi:

    ±1, ±2 og ±4

Við skulum nú athuga hverjir þessara möguleika eru lausnir.

    f(1) = 1³ − 1² – 4∙1 + 4 = 0                        1 er lausn

    f(−1) = (−1)³ − (−1)² – 4∙(−1) + 4 = 6    

    f(2) = 2³ − 2² – 4∙2 + 4 = 0                         2 er lausn

   f(−2) = (−2)³ − (−2)² – 4∙(−2) + 4 = 0        −2 er lausn

Við þurfum ekki að prófa 4 og −4 vegna þess að við höfum þegar fundið allar þrjár lausnirnar. Við getum nú þáttað jöfnuna með því að setja lausnirnar í svigana og nota gagnstætt formerki.

    x³ − x² – 4x + 4 = (x − 1)(x − 2)(x + 2) = 0

Lausnaraðferðin byggir sem sagt á því að finna þær heiltölur sem ganga upp í töluliðnum aftast og prófa hvort þær eru lausnir.

En nú getum við ekki gert ráð fyrir að allar lausnir jafna af þriðja stigi séu heiltölulausnir. Ef við hins vegar finnum eina heiltölulausn sem við getum kallað a þá segir leifareglan okkur að deiling stæðunnar með (x − a) gengur upp. Ef við framkvæmum þessa deilingu þá fáum við annars stigs jöfnu sem við getum leyst. Það gerum við t.d. með lausnarformúlunni.

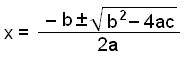
Sýnidæmi 1

Leysum jöfnuna x³ − 3x² – 2x + 4 = 0

Prófum tölurnar sem ganga upp í fjórum.

    f(1) = 1³ − 3∙1² – 2∙1 + 4 = 0                        1 er lausn

    f(−1) = (−1)³ − 3∙(−1)² – 2∙(−1) + 4 = 2     

    f(2) = 2³ − 3∙2² – 2∙2 + 4 = −4

    f(−2) = (−2)³ − 3∙(−2)² – 2∙(−2) + 4 = −12

    f(4) = 4³ − 3∙4² – 2∙4 + 4 = 12

    f(−4) = (−4)³ − 3∙(−4)² – 2∙(−4) + 4 = −100

Eina heiltölulausnin er x = 1 og til þess að ganga úr skugga um hvort jafnan hafi einhverjar fleiri lausnir deilum við með (x − 1) og skoðum hvað við getum gert við útkomuna.

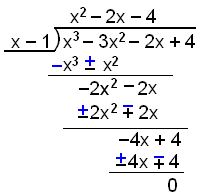
Nú getum við þáttað jöfnuna á eftirfarandi hátt:

    x³ − 3x² – 2x + 4 = (x − 1)(x² − 2x − 4) = 0

Við getum því einbeitt okkur að því að leysa jöfnuna

    x² − 2x − 4 = 0

Við vitum að hún hefur engar heiltölulausnir því við prófuðum alla möguleika hér fyrir ofan.

Við notum lausnajöfnuna við höfum a = 1, b = −2 og c = −4.

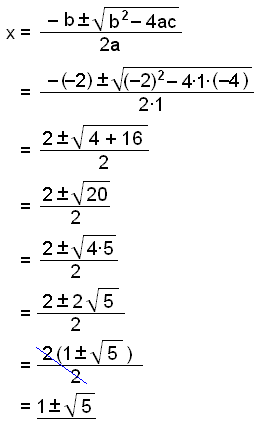
Þar með höfum við fundið allar þrjár lausnirnar á jöfnunni x³ − 3x² – 2x + 4 = 0. Þær eru eftirfarandi:

    x = 1

    x = 1 + Ö5

    x = 1 − Ö5

Sýnidæmi 2

Við getum hæglega notað þessa aðferð til þess að leysa jöfnur af fjórða stigi og hærri stigum. Leysum nú jöfnuna f(x) = x⁴ − x³ − 5x² + 3x + 2 = 0.

Prófum heiltölur sem ganga upp í aftasta stuðlinum 2. Möguleikarnir eru ±1 og ±2.

    f(1) = 1⁴ − 1³ − 5∙1² + 3∙1 + 2 = 0                       Lausn

    f(−1) = (−1)⁴ − (−1)³ − 5∙(−1)² + 3∙(−1) + 2 = −4

    f(2) = 2⁴ − 2³ − 5∙2² + 3∙2 + 2 = −4

    f(−2) = (−2)⁴ − (−2)³ − 5∙(−2)² + 3∙(−2) + 2 = 0   Lausn

Lausnirnar eru 1 og −2 þannig að deiling með x − 1 og x + 2 gengur upp. Við skulum þá deila og ná vandamálinu niður um tvö stig.

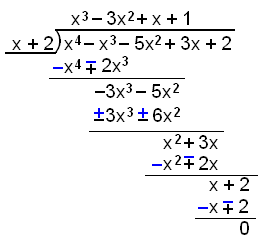
Útkomunni deilum við nú með x − 1.

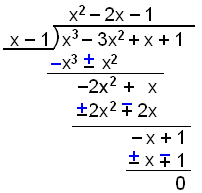
Nú höfum við þáttað f(x) = x⁴ − x³ − 5x² + 3x + 2 niður í f(x) = (x + 2)(x − 1)(x² − 2x − 1) og nú eigum við aðeins eftir að leysa jöfnuna x² − 2x − 1 = 0. Til þess notum við lausnaformúluna þar sem a = 1, b = −2 og c = −1.

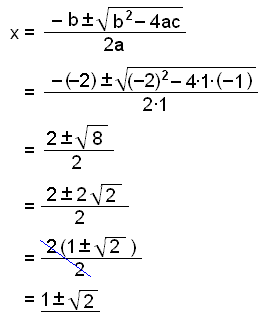
Nú höfum við loksins fundið allar lausnirnar en þær eru

    x = 1

   x = −2

   x = 1 + Ö2

   x = 1 − Ö2

Stundum getum við leyst þriðja stigs jöfnur með því að búa til sviga sem við getum tekið út fyrir alla stæðuna. Þetta gildir sérstaklega ef stuðlar margliðunnar fara kerfisbundið hækkandi. Skoðum dæmi um þetta.

Sýnidæmi 3

Leysum jöfnuna x³ − 2x² − 4x + 8 = 0

Taktu eftir því að sviginn (x − 2) er tvöfaldur í jöfnunni þegar búið er að þátta. Lausnin x = 2 er því tvöföld þannig að við höfum aðeins tvær lausnir þegar allt er talið.

Lausnir: x = 2 og x = −2.

Við höfum nú fundið rætur eða lausnir margliða þar sem stuðullinn við hæsta veldið er einn. Hvað með ef hann er einhver önnur tala? Skoðum t.d. margliðu af gerðinni f(x) = ax³ + bx² + cx + d þar sem við gerum ráð fyrir heiltölustuðlum og heiltölurótinni r. Þá gildir eftirfarandi:

    ar³ + br² + cr + d = 0

    d = − ar³ − br² − cr

    d = r(− ar² − br − c)

Þetta sýnir að rótin hlýtur að ganga upp í aftasta tölustuðlinum d burt séð frá því hvaða gildi a hefur.

Í framhaldi af þessu skulum við skoða hvort við getum fundið rætur sem eru almenn brot.

Köllum rótina r = t/n. Þá getum við haldið áfram á eftirfarandi hátt.

Ef við deilum nú í gegn með a þá fáum við eftirfarandi:

Af þessu sjáum við að t hlýtur að ganga upp í d og n hlýtur að ganga upp í a.

Almennt gildir að ef við höfum margliðu af stiginu n

   f(x) = a_nxⁿ + a_n−1xⁿ⁻¹+ ∙ ∙ ∙ ∙ + a₁x + a₀

með stuðlana a₀, a₁, a₂, ∙ ∙ ∙ ∙ ∙ a_n−2, a_n−1 og a_n

og með rótina r = ^t/_n þá gengur t upp í tölustuðlinum a₀ og n gengur upp í stuðlinum a_n sem fylgir hæsta veldinu.

Sýnidæmi 4

Leysum jöfnuna f(x) = 2x³ − 7x² + 4x + 3 = 0.

Við leitum að rótinni r = ^t/_n og við vitum að n þarf að ganga upp í 2 og getur því verið ±1 og ±2, og t þarf að ganga upp í 3 og getur því verið ±1 og ±3.

Möguleikarnir okkar eru því ±½, ±1, ±³/₂ og ±3.

Við þurfum ekki að prófa neikvæðu tölurnar vegna þess að þær gefa aðeins neikvæðar útkomur og ekki 0, en prófum hinar.

    f(½) = 2(½)³ − 7(½)² + 4∙½ + 3 = 3½

    f(1) = 2∙1³ − 7∙1² + 4∙1 + 3 = 2

    f(³/₂) = 2(³/₂)³ − 7(³/₂)² + 4∙³/₂ + 3 = 0 = lausn!

Deiling með (x − ³/₂) gengur upp í f(x), en það er dálítið óþægilegt að deila með brotum þannig að við skulum margfalda svigann með 2 og deila frekar með (2x − 3). Sú deiling á að ganga upp vegna þess að (2x − 3) = 0 ef x = ³/₂ og hlýtur því að vera þáttur í f(x).

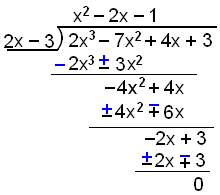
Þetta gekk upp þannig að næst er þá að leysa jöfnuna      x² − 2x − 1 = 0. Þessa jöfnu leystum við í sýnidæmi 2 þannig að við þurfum ekki að gera það aftur. Lausnirnar voru 1 + Ö2 og 1 − Ö2.

Þar með höfum við fundið allar lausnir jöfnunnar. Þær eru eftirfarandi:

    x = ³/₂ = 1½

   x = 1 + Ö2

   x = 1 − Ö2

Æfðu þig á þessum aðferðum og taktu síðan próf 2 í jöfnum III.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum