Jöfnur III
| © 2007 Rasmus ehf og Jóhann Ķsak |
Jöfnur III |
|
Kynning 3
Hvernig finnum viš skuršpunkta tveggja grafa y = f(x) og y = g(x)?
Viš kunnum nś žegar aš finna skuršpunkta grafa viš x-įsinn. Žar er y (eša hęš grafsins) = 0 og žį getum viš sett f(x) = 0 eša g(x) = 0 og leyst jöfnurnar. Ķ skuršpunkti grafa y = f(x) og y = g(x) eru bęši gröfin ķ nįkvęmlega sömu hęš yfir (eša undir) x-įsnum žannig aš viš getum bśiš til jöfnuna f(x) = g(x). Śtkoman veršur x-hnit skuršpunktsins en y-hnitiš fįum viš meš žvķ aš setja śtkomuna (x-iš okkar) inn ķ ašra hvora jöfnuna, annaš hvort ķ f(x) eša g(x).
Sżnidęmi 1
Lķtum nś į skuršpunkta tveggja lķna f(x) = 2x − 1 og g(x) = x + 1. Viš getum skošaš gröfin į eftirfarandi mynd:
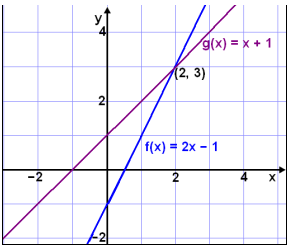
Viš skulum reikna śt lausnina meš žvķ aš leysa jöfnuna:
2x − 1 = x + 1
2x − x = 1 + 1
x = 2
Finnum sķšan y hnitiš:
f(2) = 2∙2 − 1 = 3
Skuršpunkturinn er (2, 3).
Sżnidęmiš hér fyrir ofan sżnir aš viš getum leyst jöfnur į borš viš 2x − 1 = x + 1 meš žvķ aš teikna upp vinstri hlišina sem sérstakt fall og hęgri hlišina sem sérstakt fall og lesa af skuršpunktinn. X-hnitiš er lausn jöfnunnar. Žetta kallast aš leysa jöfnur grafķskt.
Meš tilkomu grafķskra reiknivéla og töflureikna getum viš aušveldlega fundiš nįlgunargildi į lausnum jafna į grafķskan hįtt og sumar jöfnur er ekki hęgt aš leysa į annan hįtt.
Sżnidęmi 2
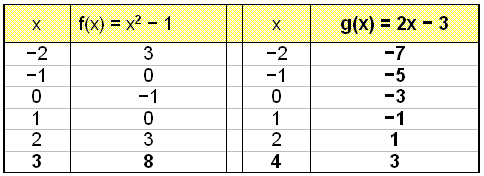
Viš skulum nś leysa jöfnuna x2 − 2x − 3 = 2x − 3. Leysum hana fyrst grafķskt og sķšan meš algebru.
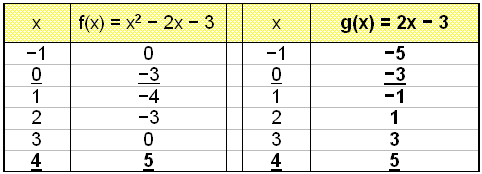
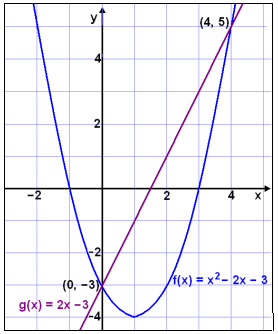
Viš sjįum bęši af grafinu og gildistöflunni aš f(x) = g(x) žegar x = 0 eša x = 4.
Meš algebru veršur lausnin svona:
x2 − 2x − 3 = 2x − 3
x2 − 4x = 0
x(x − 4) = 0
Žannig aš x = 0 eša x = 4.
Sżnidęmi 3
Leysum jöfnuna x2 − 1 = 2x − 3
Viš byrjum į žvķ aš fęra alla liši yfir į vinstri hliš jöfnunnar.
x2 − 2x + 2 = 0
Žetta leysum viš meš lausnarformślunni žar sem a = 1, b = −2 og c = 2.
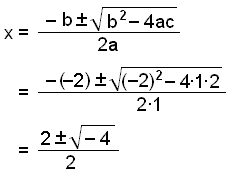
Hér fįum viš neikvęša tölu undir kvašratrótinni žannig aš jafnan er óleysanleg.
Til žess aš įtta okkur į žvķ hvaš veldur skulum viš skoša žetta į grafi.
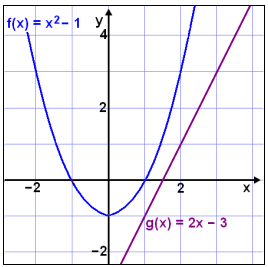
Viš sjįum aš lķnan og fleygboginn skerast ekki og žar er komin skżringin į žvķ hvers vegna jafnan er ekki leysanleg.
Sżnidęmi 4
Leysum jöfnuna x3 − 3x + 2 = x2 − 2x + 1
Sem fyrr žį byrjum viš į žvķ aš fęra alla liši yfir į vinstri hliš jöfnunnar.
x3 − 3x + 2 = x2 − 2x + 1
x3 − x2 − x + 1 = 0
(x3 − x2) − (x − 1) = 0
x2(x − 1) − (x − 1) = 0
(x − 1)(x2 − 1) = 0
(x − 1)(x − 1)(x + 1) = 0
Žetta gefur okkur ašeins tvęr lausnir, x = 1 og x = −1, en žrišja stigs jöfnur hafa oft žrjįr lausnir. Skošum į grafi hverju žetta sętir.
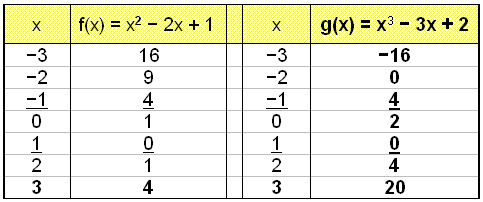
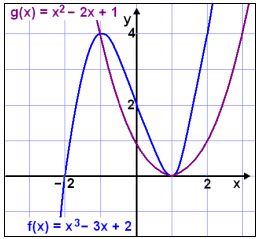
Viš sjįum į grafinu og ķ gildistöflunum aš gröfin skerast ašeins į tveimur stöšum. Jafnan hefur lausnirnar x = −1 og x = 1.
Sżnidęmi 5
Leysum jöfnuna x2 = Öx
Viš sjįum fljótlega aš x = 0 og x = 1 eru
lausnir, en eru lausnirnar fleiri? Žaš er ólķklegt en viš skulum skoša gröfin.
Köllum vinstri hlišina f(x) = x2 og hęgri hlišina g(x) = Öx, en munum aš g(x) getur ekki tekiš į móti neikvęšum tölum žannig aš neikvęšar lausnir koma ekki til greina.

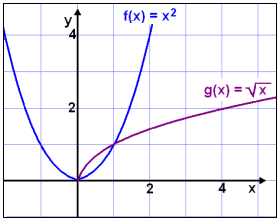
Grafiš upplżsir aš lausnirnar eru ašeins žessar tvęr eša x = 0 og x = 1. Svona mį hins vegar reikna žetta:
| x2 = Öx
x4 = x x4 − x = 0 x(x3 − 1) = 0 |
Hefjum
bįšar hlišar jöfnunnar ķ annaš veldi til žess aš eyša ferningsrótinni.
|
Žetta gefur lausnirnar x = 0 og x = 1.
Sżnidęmi 6
Leysum jöfnuna ln x = x2 − 1
Žessa jöfnu getum viš ekki leyst meš góšu móti en viš gętum dottiš ofan į žaš eftir dįlķtiš grufl aš x = 1 gefur nśll į bįšum hlišum jöfnunnar og er žvķ lausn. Žį er spurning hvort ašrar lausnir eru til. Skošum žaš į grafi.

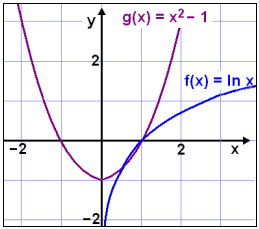
Grafiš sżnir aš lausnirnar eru tvęr. Önnur lausnin er nįkvęmlega x = 1 vegna žess aš ef viš setjum veldisvķsinn 0 į grunntöluna e žį fįum viš śt 1.
Taktu eftir žvķ hvernig viš getum žétt śtreikningana ķ gildistöflunni žegar tölurnar ķ śtkomudįlkunum taka aš nįlgast. Meš žvķ aš žétta žetta enn meir žį getum viš fundiš eins nįkvęma lausn og viš žurfum į aš halda.
| Sżnidęmi 7 |
 |
EXCEL
|
Leysum jöfnuna ln x = x2 − 1 meš reiknitękjum.
Ef viš höfum ašgang aš grafķskum reiknivélum žį getum viš teiknaš gröf hęgri og vinstri hlišar ķ sama hnitakerfiš (sjį föll I, kynning 1) og notaš Zoom (shift F2)og sķšan Trace (shift F1) til žess aš finna nįlgun į lausnunum.
Töflureiknirinn EXCEL hefur sérstakt verkfęri (goal seek) til žess aš leysa svona jöfnur, en ef viš ętlum aš nżta okkur žaš žį er best aš snśa jöfnunni fyrst žannig aš ein tala verši į vinstri hliš.
ln x = x2 − 1
1 = x2 − ln x
Viš skulum nś fara ķ EXCEL og byrja į žvķ aš skrifa upphafsgildi x eša upphaf leitarinnar ķ reit B2. Viš getum t.d. haft žaš 0,1. Sķšan setjum viš hęgri hlišina jöfnunnar ķ reit D2 og notum umsnśninginn x2 − ln x, en hann kom śt hér fyrir ofan. Ķ reit D2 kemur žį eftirfarandi formśla:
= B2^2−ln(B2)
Nś veljum viš Toolsog sķšan Goal Seek en žį kemur upp eftirfarandi valmynd:
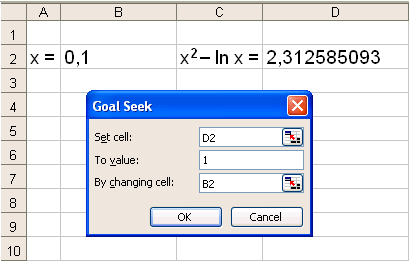
Hér skrifum viš D2, 1 og B2 ķ gluggana į valmyndinni. Meš žvķ bišjum viš EXCEL aš lįta reit D2 (set cell D2) verša 1 (To value 1) meš žvķ aš breyta x-inu ķ reit B2 (By changing cell B2). Ef viš nś veljum OK žį birtast eftirfarandi upplżsingar:
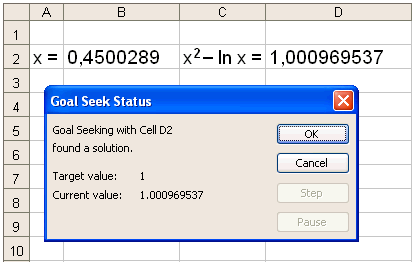
Žetta segir okkur aš nįlgunin
x ≈ 0,45 sem viš fundum ķ sżnidęmi 6 er bżsna góš. EXCEL finnur lķtiš
betri lausn eša x ≈ 0,4500289.
Ęfšu žig į žessum ašferšum og taktu sķšan próf
3 ķ jöfnum III.
ps. mundu eftir aš fylla śt ķ tékklistann žinn jafnóšum