© 2007 Rasmus ehf og Jóhann Ísak
Ójöfnur I
© 2007 Rasmus ehf og Jóhann Ísak |
Ójöfnur I |
|
Lausn ójöfnu felst í því að finna tölu eða bil á talnalínunni sem uppfyllir ákveðin skilyrði. Þessi skilyrði eru sett með eftirfarandi merkjum sem við getum kallað ójöfnumerki.
> merkir stærra en
< merkir minna en
merkir stærra en eða jafnt og
merkir minna en eða jafnt og
Fullyrðingin 3 > 2 (þrír er stærri en 2) er sönn fullyrðing og við getum munað hvernig merkið á að snúa út frá því að merkið bendir alltaf á minni töluna. Þannig er fullyrðingin 2 < 3 (tveir er minna en 3) einnig sönn.
Ef við segjum x > 2 meinum við í flestum tilfellum allar rauntölur sem eru fyrir ofan tvo. Nákvæmar er að segja {xÎR | x > 2} vegna þess að þá tökum við fram að við erum að tala um allar rauntölur fyrir ofan 2.
Ef við hins vegar segjum x
2 þá meinum við 2 og
allar tölur þar fyrir ofan. Munurinn er sá að 2 teljast með.
Við getum í mörgum tilvikum notað sömu aðferðir til þess að leysa ójöfnur og við notum til þess að leysa jöfnur. Við getum t.d. lagt við og dregið frá stærðir sitt hvoru megin við ójöfnumerkið og margfaldað og deilt með jákvæðum tölum. Lítum á sýnidæmi.
Leysum eftirfarandi ójöfnu:
 |
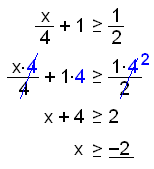Við margföldum fyrst alla liði í jöfnunni með 4 til þess að eyða brotunum. Síðan drögum við 4 frá báðum hliðum. |
Í fljótu bragði virðumst við geta notað kunnáttu okkar í jöfnureikningi til þess að leysa ójöfnur, en það er því miður ekki rétt. Nokkrar undantekningar eru hér á og sú algengasta er margföldun eða deiling með neikvæðri tölu. Skoðum eftirfarandi:
Við sjáum af talnalínunni hér fyrir ofan að a < b. Ef við hins vegar margföldum báðum megin með −1 þá verður ójafnan ekki lengur sönn nema að við snúum við ójöfnumerkinu þannig að ójafnan verði −a > −b, enda er −b lengra til vinstri á talnalínunni en −a. ( Ef 5 >3 og margföldum með -1 þá fáum við -5 > -3 sem er ekki rétt við snúm því ójöfnumerkinu og fáum -5 < -3 )
Ef við margföldum eða deilum í alla liði í ójöfnu með neikvæðri stærð þá verðum við að snúa ójöfnumerkinu.
2 − x > 1 −x > −1 x < 1 |
Við drögum 2 frá báðum hliðum. Síðan margföldum við báðum megin með −1 og munum eftir því að snúa ójöfnumerkinu. |
Við getum snúið við brotastrikum á báðum hliðum jafna en það gengur ekki þegar við vinnum með ójöfnur.
Ef a < b þá er 1/a > 1/b vegna þess að deiling með stærri tölunni gefur minni útkomu. Ef við hins vegar munum eftir því að snúa ójöfnumerkinu þá er þetta í lagi.
 |
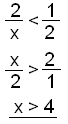Við veltum brotastrikinu báðu megin og munum að snúa ójöfnumerkinu. Loks margföldum við í gegn með samnefnaranum 2 . |
Þetta má einnig leysa á eftirfarandi hátt:
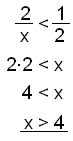
Það er fleira sem er varhugavert þegar við leysum ójöfnur. Það er t.d. varasamt að hefja báðar hliðar ójöfnu í annað veldi ef önnur hliðin reynist neikvæð. Ekki er leyfilegt að beita föllum á báðar hliðar ójöfnu nema að ljóst sé að fallið sé vaxandi fyrir allar tölur eða á því bili sem unnið er með hverju sinni.
En hvað er átt við með vaxandi falli ? Hér fyrir neðan eru gröf nokkurra slíkra falla en þau má nota til að leysa ójöfnur.
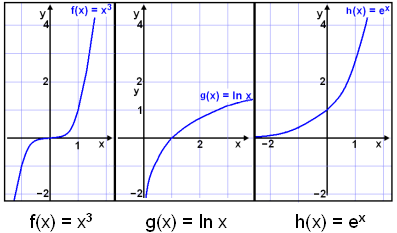
Föllin f(x) = x3, g(x) = ln x og h(x) = ex fara öll vaxandi með hækkandi x-i eins og gröfin sýna. Þessi föll og fleiri slík má nota til þess að leysa ójöfnur, en fallið g(x) = ln x takmarkast þó við jákvæðar tölur.
Leysum ójöfnuna |
 |
Hér hefjum við hiklaust báðar hliðar í þriðja veldi og fáum
x
8
Leysum ójöfnuna ln (2x − 1) < ln 3. Ath. Fallið ln x er aðeins skilgreint ef x > 0
Hér setjum við hiklaust báðar hliðar sem veldisvísa á e og upphefjum þannig ln-fallið. Við fáum eftirfarandi:
2x -1 > 0 |
2x − 1 < 3 |
2x > 1 x > 1/2 |
2x < 4 x < 2 |
Af þessu sést að 1/2 < x < 2
Leysum ójöfnuna ex > e−x.
ex > e−x (ex)2 > 1 e2x > 1 2x > 0 x > 0 |
Hér
margföldum við fyrst báðar hliðar með ex Hér tökum við ln af báðum hliðum. |
Æfðu þig á þessum aðferðum og taktu síðan próf
1 í ójöfnum.
ps. mundu eftir að fylla út í tékklistann þinn jafnóðum