ę 2007 Rasmus ehf og Jˇhann ═sak
ę 2007 Rasmus ehf og Jˇhann ═sak |
Ëj÷fnur I |
|
Hvernig leysum vi ˇj÷fnuna x2 − 1
![]() 0? Vi getum leyst
samsvarandi j÷fnu en ■ß fßum vi tvŠr lausnir.
0? Vi getum leyst
samsvarandi j÷fnu en ■ß fßum vi tvŠr lausnir.
x2 − 1 = 0
(x + 1)(x − 1) = 0
Lausnir: x = 1 og x = −1.
Vi getum sem sagt fundi hvar stŠan er n˙ll en eftir stendur a finna hvar h˙n er minni en n˙ll. Me ÷rum orum, vi ■urfum a finna hvar h˙n er neikvŠ. Vi skulum n˙ skoa formerki ■ßttanna (x + 1) og (x − 1) og nota talnalÝnuna sem vimi fyrir x-in sem vi setjum inn Ý svigana.
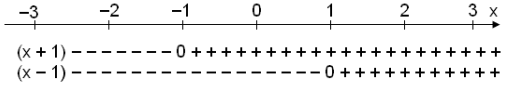
Vi h÷fum n˙ merkt ■au svŠi me + ■ar sem ˙tkoman ˙r vikomandi sviga er jßkvŠ og me − ■ar sem h˙n er neikvŠ, en hvernig getum vi nřtt ■etta til ■ess a leysa upphaflegu ˇj÷fnuna?
J˙, vi vitum a vinstri hli ˇj÷fnunnar er margfeldi sviganna.
(x + 1)(x − 1) = x2 − 1
Vi vitum einnig a −∙− = + og +∙− = − ■annig a ˙tkoman verur jßkvŠ ■ar sem svigarnir hafa sama formerki, en ■ar sem formerkin eru gagnstŠ ■ar verur ˙tkoman neikvŠ og ■ar hefur ˇjafnan lausn.
Vi skulum n˙ fullgera formerkjak÷nnunina.
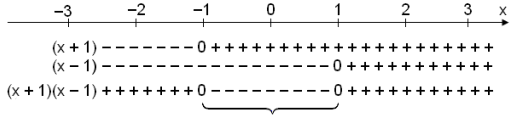
┴ ■essu bili er lausnin.
−1
![]() x
x
![]() 1
1
Athugum n˙ hvernig vi getum gengi beint til verks ßn ■ess a ■ßtta vinstri hliina.
Vi setjum niur n˙llpunktana fyrst og prˇfum sÝan hvaa formerki fŠst me ■vÝ a velja eitthvert gildi ß x ß milli n˙llst÷vanna.
Ef vi veljum t.d. x = 0 (■a er einfaldast) ■ß fßum vi eftirfarandi:
Ef f(x) = x2 − 1 ■ß er f(0) = 02 − 1 = −1.
Ůar me h÷fum vi fundi ˙t a f(x) = x2 − 1 gefur neikvŠar ˙tkomur ß bilinu −1
![]() x
x
![]() 1 og formerkjak÷nnunin
verur bara svona:
1 og formerkjak÷nnunin
verur bara svona:

lausn
Vi getum einnig lesi lausnina af grafi.
Lausn ˇj÷fnunnar x2 − 1
![]() 0
birtist ■ar sem graf f(x) = x2 − 1 sker x-ßsinn og er undir honum. Skoum ■etta ß mynd.
0
birtist ■ar sem graf f(x) = x2 − 1 sker x-ßsinn og er undir honum. Skoum ■etta ß mynd.
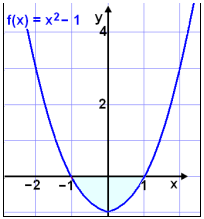
Grafi er undir og ß x-ßsnum ß bilinu
−1
![]() x
x
![]() 1 (sjß litaa svŠi).
1 (sjß litaa svŠi).
Hva ef ˇj÷fnumerki snÚri ß hinn veginn og
ˇjafnan hefi veri x2 −
1
![]() 0?
0?
Ůß lŠsum vi af grafinu hvar graf f(x) er fyrir ofan x-ßsinn ea lŠsum ˙r formerkjak÷nnuninni hvar stŠan er jßkvŠ.
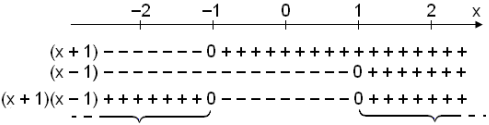
Lausn: x
![]() −1 Lausn: x
−1 Lausn: x
![]() 1
1
Lausnin ß ˇj÷fnunni x2 − 1
![]() 0 er ■vÝ
sitt hvor hlutinn af talnalÝnunni x
0 er ■vÝ
sitt hvor hlutinn af talnalÝnunni x
![]() −1
ea x
−1
ea x
![]() 1.
1.
Leysum ˇj÷fnuna x2 − 2x − 3 < x + 1.
Leysum fyrst j÷fnuna x2 − 2x − 3 = x + 1
x2 − 2x − 3 = x + 1
x2 − 3x − 4 = 0
(x + 1)(x − 4) = 0
Lausnir: x = −1 og x = 4
Gerum n˙ formerkjak÷nnun.
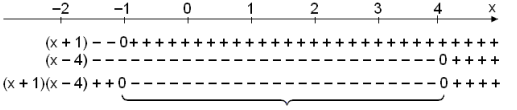
Lausn: −1 < x < 4
Skoum ■etta einnig ß grafi. Lausnin hlřtur a koma fram ■ar sem vinstri hliin f(x) = x2 − 2x − 3 er undir (minni en) g(x) = x + 1 (sjß litaa svŠi).
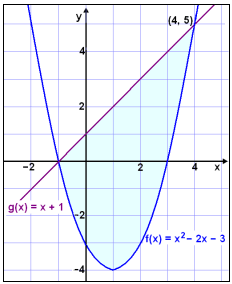
Leysum ˇj÷fnuna ![]()
Vi skulum byrja ß ■vÝ a gera formerkjak÷nnun fyrir svigana (x + 1) og (x − 1). Vi ■urfum a muna eftir ■vÝ a sams konar reglur gilda um formerki Ý margf÷ldun og deilingu (−/− = + og −/+ = −). Mismunandi formerki gefa mÝnus en eins formerki gefa pl˙s.
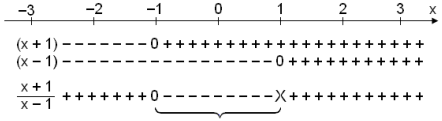
Lausn
En n˙ ■urfum vi a gß
a okkur. X-i getur ekki ori 1 vegna ■ess a ■ß er deilt me n˙lli.
Lausnin er ■vÝ −1
![]() x < 1.
x < 1.
Skoum n˙ ■etta ß grafi en gerum fyrst gildist÷flu.
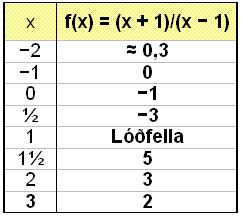 |
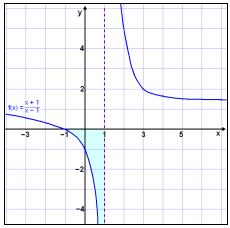 |
Grafi hefur lˇfellu Ý x = 1 og er fyrir nean x-ßsinn ß bilinu −1 til 1 (sjß litaa svŠi).
Leysum ˇj÷fnuna
Vi byrjum ß ■vÝ a fß n˙ll ß vinstri hli ˇj÷fnunnar ■annig a vi getum nota formerkjak÷nnun til ■ess a leysa ˇj÷fnuna.
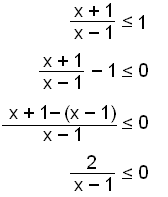 |
HÚr setjum vi ß eitt strik og einf÷ldum. |
SÝan gerum vi formerkjak÷nnun.
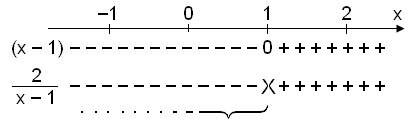
Lausn x < 1
N˙ skulum vi skoa ■etta ß grafi og teikna upp hŠgri og vinstri hli ˇj÷fnunnar. Vinstri hliin er s˙ sama og Ý sřnidŠmi 2 en hŠgri hliin er lÝnan g(x) = 1 (lßrÚtt lÝna Ý hŠinni 1).
Leysum ˇj÷fnuna x2 <
![]() x.
x.
Jafnan x2 =
![]() x hefur
aeins lausnirnar x = 0 og x = 1.
x hefur
aeins lausnirnar x = 0 og x = 1.
x2 <
![]() x
x
x2 −
|
Vi fŠrum fyrst alla lii yfir ß vinstri hli. |
Prˇfum n˙ einhverja t÷lu ß milli n˙llst÷vanna, t.d. ╝.
f(x) = x2 −
![]() x
x
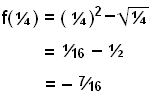
Vi fßum neikvŠa ˙tkomu ■annig a formerkjak÷nnunin verur eftirfarandi:
![]()
![]() ekki
til
ekki
til ![]()
Lausn: 0 < x < 1
Skoum ■etta n˙ ß grafi.
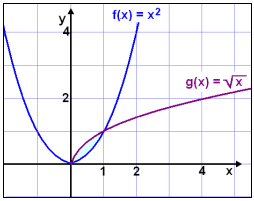
┴ bilinu 0 til 1 er graf f(x) = x2 fyrir nean graf g(x) =
![]() x (sjß
litaa svŠi).
x (sjß
litaa svŠi).
Leysum ˇj÷fnuna ln x
![]() ln 1/x.
ln 1/x.
Vi einf÷ldum eins og kostur er og fßum n˙ll ß hŠgri hli til ■ess a geta nota formerkjak÷nnun.
ln x
![]() ln 1/x
ln 1/x
x
![]() 1/x
1/x
x2
![]() 1
1
x2 − 1
![]() 0
0
(x
+ 1)(x − 1)
![]() 0
0
N˙ getum vi gert formerkjak÷nnun, en aeins fyrir jßkvŠ x vegna ■ess a ln-falli er ekki til fyrir neikvŠ x.
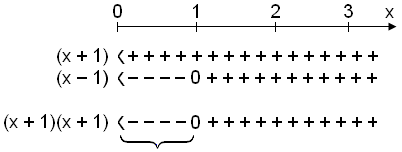
Lausn: 0 < x
![]() 1
1
Vi skulum n˙ skoa ■etta ß grafi.
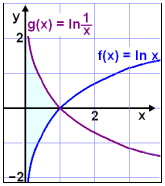
Vi sjßum a graf f(x) er undir grafi g(x) (sjß litaa svŠi) ß bilinu 0 til 1, en n˙lli getur ekki veri me Ý lausninni vegna ■ess a ln 0 er ekki til og ■a mundi valda deilingu me n˙lli ß hŠgri hli upphaflegu ˇj÷fnunnar.
Ăfu ■ig ß ■essum aferum og taktu sÝan prˇf
2 Ý ˇj÷fnum.
ps. mundu eftir a fylla ˙t Ý tÚkklistann ■inn jafnˇum