© 2007  Rasmus ehf    og Jóhann Ísak

Ójöfnur.

Kynning 3   Tölugildi

Fjarlægð punktsins x á talnalínunni frá núllpunktinum kallast tölugildi x og er táknað |x|.

Ef x = 2 þá er fjarlægðin frá núllpunktinum = |2| = 2.

Ef x = −2 þá er fjarlægðin frá núllpunktinum = |−2| = 2.

Fjarlægðin á milli tveggja punkta á talnalínunni er b − a ef b > a og a − b ef b < a. En ef við vitum ekki hvor talnanna a eða b er stærri þá getum við sagt að fjarlægðin sé  |a − b|.

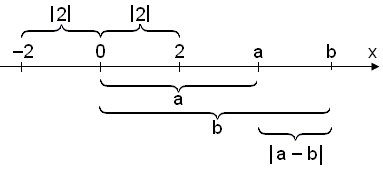
Við getum hugsað okkur að þegar við nýtum okkur tölugildi þá séum við að nota talnalínuna eins og málband og þá skiptir ekki máli hvort við mælum frá hægri til vinstri eða frá vinstri til hægri.

Tölugildi skiptir um formerki (eða hendir í burtu mínusnum) ef við fáum neikvæða stærð innan tölugildis merkisins.

Sýnidæmi 1

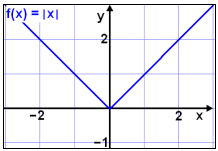
Teiknum graf fallsins f(x) = |x|.

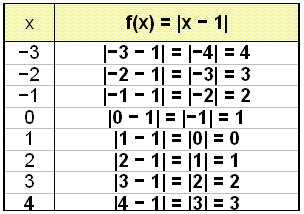
Setjum upp gildistöflu og teiknum síðan grafið.

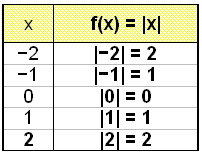Sýnidæmi 2

Teiknum graf fallsins f(x) = |x − 2| − |x|.

Setjum upp gildistöflu og teiknum síðan grafið.

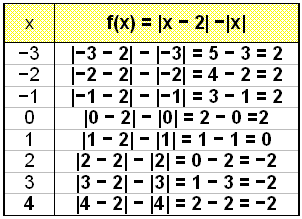Við munum eftir því að skipta um formerki ef við fáum neikvæða stærð innan tölugildismerkisins.

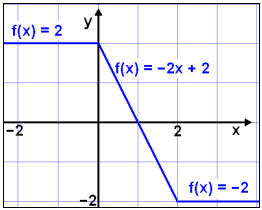
Tökum eftir því að grafið sýnir í raun þrjá línubúta.

Fyrir x < 0 gildir að stærðirnar innan beggja tölugildanna gefa neikvæða útkomu og í báðum tilfellum er skipt um formerki. Það getum við gert með því að margfalda stærðirnar með −1.

Fallið verður þá eftirfarandi ef x < 0:

    f(x) = (−1)∙(x − 2) − (−1)∙(x) = −x + 2 + x = 2

Á bilinu 0  x < 2 er formerkinu breytt á fyrra tölugildinu en ekki því seinna.

    f(x) = (−1)∙(x − 2) − x = −2x + 2

Þegar x   2 Þurfum við ekki að breyta neinum formerkjum og getum fellt niður tölugildin.

   f(x) = (x − 2) −(x) = x −2 −x = − 2

Tökum einnig eftir því að jafnan |x − 2| − |x| = 2 hefur öll x  0 sem lausnir en jafnan |x − 2| − |x| = 0 hefur aðeins lausnina x = 1.

Sýnidæmi 3

Leysum ójöfnuna |x − 1| < 4.

Vendipunkturinn í þessari ójöfnu er x = 1. Við getum litið á dæmið sem tvær ójöfnur og skilin eru við x = 1. Við skulum því leysa þetta í tvennu lagi.

             Breytt formerki.              Óbreytt formerki.

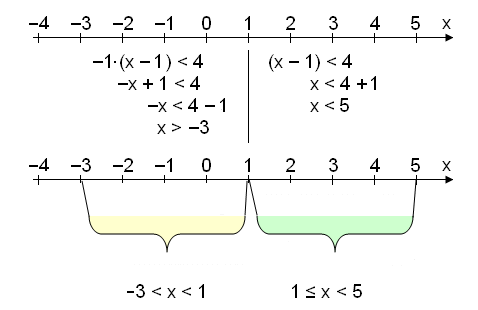
Við skulum nú skoða hvað ójafnan |x − 1| < 4 merkir.

|x − 1| táknar fjarlægð x frá einum.

|x − 1| < 4 segir að fjarlægðin frá 1 verður að vera innan við 4.

Þetta passar við lausnina hér fyrir ofan.

En leysum þetta nú grafískt.

Þá skoðum við hvenær graf f(x) = |x − 1| er neðan við línuna g(x) = 4.

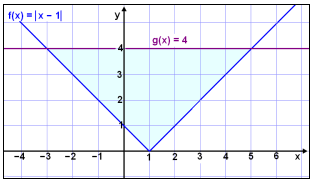Lausnin kemur fram þar sem graf f(x) = |x − 1| er fyrir neðan línuna g(x) = 4 (sjá litaða svæðið),
en það er á bilinu −3 < x < 5.

Sýnidæmi 4

Leysum ójöfnuna |x + 2| > |2x − 8|.

Sem fyrr leysum við hana í þremur hlutum.

Vendipunktar eru í x = −2 þar sem fyrra tölugildið breytir formerkjum og í x = 4 þar sem seinna tölugildið breytir formerkjum.

Formerkjabreytingar í fyrri og seinni tölugildissviga:

Breytist í báðum.      Breytist í seinni.     Breytist í hvorugum.

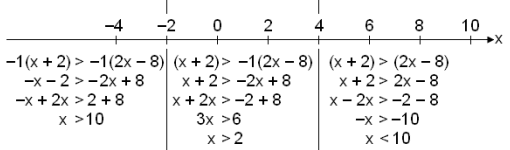x > 10 er ekki lausn vegna þess að þessir útreikningar gilda fyrir x sem eru fyrir neðan −2. Á þessu bili er því engin lausn.

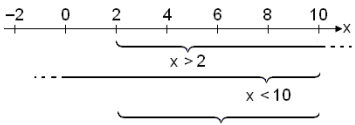                                                                            Lausn: 2 < x < 10

Við skulum nú leysa dæmið grafískt.

Við byrjum á því að gera gildistöflur fyrir bæði föllin.

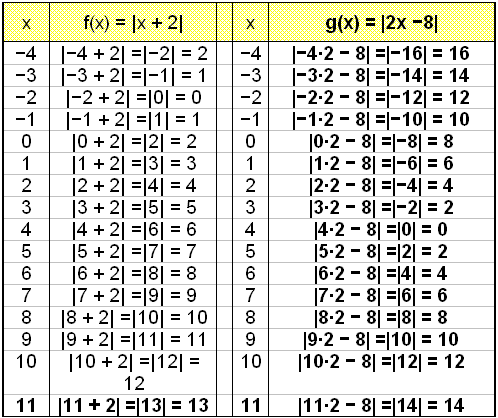
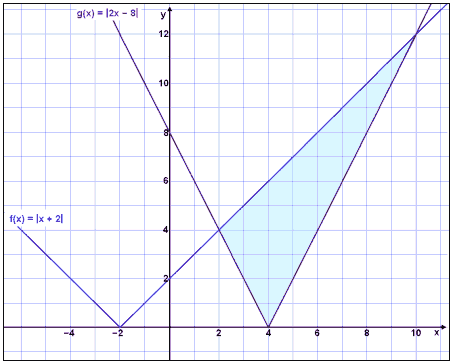
Við sjáum á grafinu að f(x) = |x + 2| er fyrir ofan g(x) = |2x − 8| frá x = 2 til x = 10 (sjá litaða svæðið).

Lausnin er 2 < x < 10.

Æfðu þig á þessum aðferðum og taktu síðan próf 3 í ójöfnum.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum