© 2007  Rasmus ehf    og Jóhann Ísak

Regla Pýþagórasar

Kynning 2    Jöfnur, fjarlægðir og miðpunktar

 

Þegar við nýtum okkur Pýþagórasarreglu leiðir það oft til jafna af fyrsta og öðru stigi. Skoðum nokkur dæmi.

Sýnidæmi 1

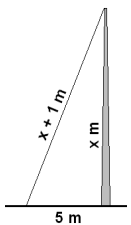
Mastur er stagað með vír sem er einum metra lengra en mastrið sjálft. Stagið er fest 5 m aftan við mastrið. Hve hátt er mastrið? 

Við byrjum á því að teikna þetta upp til þess að átta okkur á dæminu. Við köllum hæð mastursins x og lengd vírsins x + 1. Síðan gerum við ráð fyrir að mastrið standi því sem næst beint þannig að við getum notað Pýþagórasarreglu.

    52 + x2 = (x + 1)2

    25 + x2 = x2 + 2x + 1

    25 − 1 = 2x

                x = 24/2 = 12 m

Sýnidæmi 2

Þríhyrningur hefur hornin 45°, 45° og 90° og langhlið sem er 10 cm. Notum Pýðagórasarreglu til þess að finna skammhliðarnar.

Við byrjum á því að teikna mynd.

       

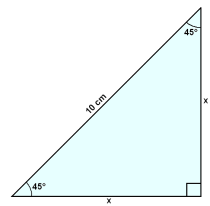
Notum Pýþagórasarreglu á þennan þríhyrning.

    x2 + x2 = 102

            2x2 = 100

          x2 = 50

           x ≈ 7

Sýnidæmi 3

Kringlótt linsa úr stjörnukíki er 34 cm í þvermál. Linsan hefur kúpt yfirborð og er þykktin mest 1 cm í miðjunni. Kúpta yfirborðið er hluti hringferils. Notum Pýþagórasarreglu til þess að finna radíus þess hrings.

Við byrjum á því að teikna mynd sem útskýrir dæmið.

       

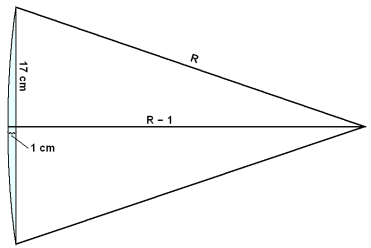
Nú getum við sett upp regluna.

                   172 + (R − 1)2 = R2

             289 + R2 − 2R + 1 = R2

                                    −2R = −289 − 1

                                        R = 290/2 = 145 cm

Sýnidæmi 4

Finnum hvaða rétthyrndur þríhyrningur hefur skammhlið sem er tveimur cm lengri en hin skammhliðin og tveimur cm styttri en langhliðin.

Teiknum fyrst mynd.

       

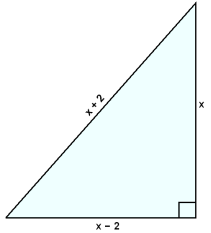
Nú beitum við Pýþagórasarreglu.

        (x − 2)2 + x2 = (x + 2)2

   x2 − 4x + 4 + x2 = x2 + 4x + 4

                x2 − 8x = 0

               x(x − 8) = 0

Hér fáum við tvær lausnir, x = 0 og x = 8.

Lausnin x = 0 kemur ekki til greina þannig að rétta lausnin er að skammhliðin sem um ræðir er 8 cm. Hin skamhliðin er 6 cm og langhliðin er 10 cm.

Sýnidæmi 5

Finnum fjarlægðina á milli punktanna A = (−3, −3) og B = (5, 3) í hnitakerfi. Notum einingar hnitakerfisins (lengd rúðu) sem mælieiningu.

Teiknum þetta fyrst upp.

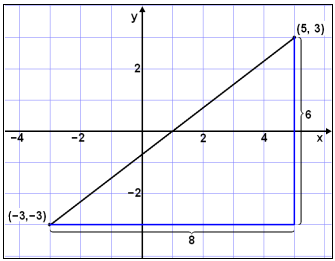
Hefð er fyrir því að nota tölugildismerki til að tákna lengd eða fjarlægð. Við skulum því tákna fjarlægðina á milli A og B með |AB|. Við sjáum að við getum reiknað |AB| með því að draga línu á milli punktanna og hugsa okkur hana sem langhlið í rétthyrndum þríhyrningi. Lengdir skammhliðanna getum við talið út eða reiknað með því að finna mismun x-hnitanna annars vegar og hins vegar y-hnitanna.

   5 − (−3) = 8

   3 − (−3) = 6

Nú getum við notað Pýþagórasarreglu til þess að finna langhliðina .

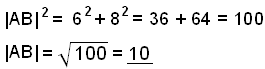
Við getum nú sett upp almenna formúlu til þess að finna fjarlægðina á milli tveggja punkta í hnitakerfi í samræmi við sýnidæmið hér fyrir ofan.

Köllum punktana A = (x1, y1) og B = (x2, y2).

Mismunur hnitanna verður þá x2 − x1 og y2 − y1.

Með Pýþagórasarreglu verður fjarlægðarformúlan eftirfarandi:

               

Sýnidæmi 6

Við skulum nú finna hvaða punktar (x, y) eru jafn langt frá punktunum A = (1, 7) og B = (5, 3).

Þá getum við sett upp eftirfarandi jöfnu:

            Fjarlægðin frá (1, 7) = fjarlægðin frá (5, 3).

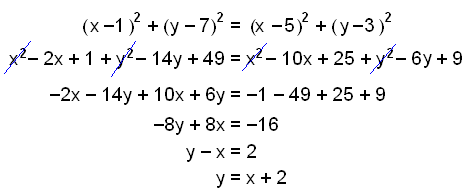
Hér fáum við jöfnu línu. Við skulum skoða þetta á grafi.

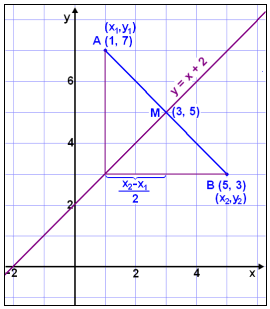
Línan er mitt á milli A og B og inniheldur þá punkta sem eru jafn langt frá A og B. Slík lína kallast miðnormall eða miðþverill á línustrikið AB. Línan sker miðpunkt AB undir 90° horni. 

Við getum einnig fundið miðþveril með því að finna miðpunkt línunnar AB fyrst og finna síðan línu sem sker þann punkt og er hornrétt á línu í gegnum A og B.

En hvernig finnum við þá miðpunkt AB?

Ef við hugsum okkur rétthyrndan þríhyrning með langhliðina AB og tökum tillit til rimareglunnar. Þá sjáum við að við þurfum að bæta við x-hnit A helmingnum af mismuni x-hnita A og B (sjá myndina hér fyrir ofan).

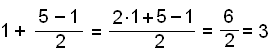
Ef við reiknum með bókstöfum verður þetta svona:

Þetta er ekkert annað en meðaltal x-hnitanna. Sams konar útreikninga getum við síðan gert til að finna y-hnitið. Niðurstaðan er að við getum fundið miðpunkt línustriksins AB með því að finna meðaltal x- og y-hnita A og B.

Reglan verður eftirfarandi:

           

Sýnidæmi 7

Finnum nú miðþverilinn í sýnidæminu hér fyrir ofan með því að nota hallatölu og miðpunkt.

Hallatalan á milli A og B er eftirfarandi:

    k = (y2 − y1)/ (x2 − x1) = (3 − 7)/(5 − 1) = −4/4 = −1

    Hornrétt hallatala er k = 1.

    M = ((5 + 1)/2, (3 + 7)/2) = (3, 5)

Nú notum við punkthallajöfnuna y = k(x − x1) + y1 til þess að finna jöfnu þverilsins.

   y = 1(x − 3) + 5

   y = x − 3 + 5

   y = x + 2

Æfðu þig á þessum aðferðum og taktu síðan próf 2 í reglu Pýþagórasar.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum