© 2007 Rasmus ehf og Jóhann Ísak
© 2007 Rasmus ehf og Jóhann Ísak |
Regla Pýþagórasar |
|
Skoðum nú hvaða punktar það eru sem liggja nákvæmlega í sömu fjarlægð frá einhverjum tilteknum miðpunkti. Hvernig getum við notað Pýþagórasarreglu til þess að finna tengsl slíkra punkta?
Tökum t.d. þá punkta sem eru í fjarlægðinni 5 frá miðju hnitakerfisins. Vegna þess að miðjan er í (0, 0) þá þurfum við ekki að finna mismun hnitanna og við getum sagt að punktarnir verði að uppfylla eftirfarandi skilyrði Pýþagórasarreglu:
x2 + y2 = 52
Við sjáum að heiltölupör sem uppfylla þessi skilyrði eru ±3 og ±4 ásamt 0 og ±5. Teiknum þessa punkta upp í hnitakerfi og rétthyrndu þríhyrningana sem þeir mynda með ásum hnitakerfisins.
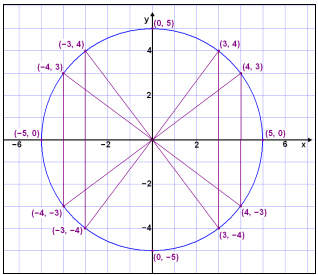
Við sjáum að punktarnir eru allir á hring með miðju í (0, 0) og með radíus 5. Aðrir punktar á hringnum eru með ræð hnit sem uppfylla skilyrðin x2 + y2 = 52. Almennt gildir að allir punktar sem eru í fjarlægðinni r frá tilteknum miðpunkti liggja á hring með radíus r.
En getum við búið til fall úr Pýþagórasarreglu og teiknað eftir því graf sem er eins og hringurinn á myndinni eða aðrir hringir? Leysum jöfnuna m.t.t. y og skoðum málið.
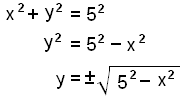
Þetta er ekki fall, enda sker lóðrétt lína eins og y-ásinn hringinn á tveimur stöðum. Hins vegar getum við skipt þessu upp í eftirfarandi tvö föll:
og |
F(x) gildir þá fyrir efri hluta hringsins, þann hálfhring sem er yfir x-ásnum, og g(x) fyrir neðri hlutann.
Finnum jöfnu hrings sem hefur miðju í (−2, 0) og radíus 5.
Þetta er sams konar hringur og á myndinni hér fyrir ofan, en nú byrjar hann tveimur einingum fyrr (til vinstri) í hnitakerfinu.
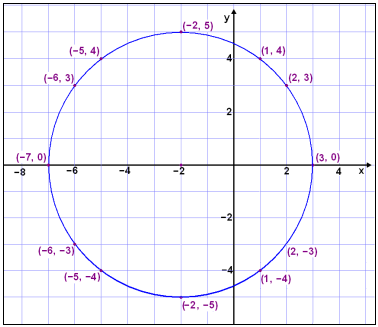
Punktarnir á hringnum eru allir í fjarlægðinni 5 frá punktinum (−2, 0). Þeir hljóta að hafa x-hnit sem eru alltaf tveimur lægri en hnitin í hringnum x2 + y2 = 52, t.d. (−6, 3) í stað (−4, 3), (−5, 4) í stað (−3, 4) o.s.frv. Ef við reiknum fjarlægð þessara punkta frá (−2, 0) fáum við eftirfarandi með reglu Pýþagórasar:
(−6 − (−2))2 + (3 − 0)2 = 16 + 9 = 25 = 52
(−5 −(−2))2 + (4 − 0)2 = 9 + 16 = 25 = 52
o.s.frv.
Ef við reiknum þetta með breytunum x og y fáum við eftirfarandi:
(x −(−2)2 + (y − 0)2 = 52
(x + 2)2 + y2 = 52
Síðan getum við margfalda upp svigann og sameinað tölurnar.
x2 + 4x + 4 + y2 = 25
x2 + 4x + y2 = 21
Finnum jöfnu hrings með miðju í (2, 2) og radíus 2.
Setjum upp Pýþagórasarreglu fyrir alla punkta (x, y) sem eru í 2 eininga fjarlægð frá punktinum (2, 2).
(x − 2)2 + (y − 2)2 = 22
Margföldum upp úr svigunum og sameinum tölurnar:
x2 − 4x + 4 + y2 − 4y + 4 = 4
x2 − 4x + y2 − 4y = −4
Við sjáum af útreikningunum hér fyrir ofan að almenn jafna sem lýsir hring með miðju í punktinum (a, b) og radíus r er eftirfarandi:
![]()
Hins vegar getur þessi jafna verið dulbúin ef búið er að margfalda upp úr svigunum og sameina tölurnar.
Finnum ferilinn sem jafnan x2 − 6x + y2 − 4y = 3 tjáir.
Hér skulum við bæta inn í jöfnuna hálfum stuðlinum við x höfnum í annað veldi (32) og hálfum stuðlinum við y höfnum í annað veldi (22). Eftir það getum við notað regluna a2 ± 2ab + b2 = (a ± b)2 til þess að búa til sviga í öðru veldi.
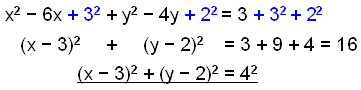 |
Við verðum að bæta sömu tölum við beggja vegna. |
Þetta er hringur með miðju í punktinum (3, 2) og radíus 4.
Finnum hvar hringurinn (x + 3)2 + y2 = 52 sker ása hnitakerfisins.
Á x-ásnum eru y-hnitin 0 þannig að við getum sett 0 inn í jöfnuna fyrir y til þess að finna hvar hringurinn sker x-ásinn.
(x + 3)2 + 02 = 52
(x + 3)2 = 52
x + 3 = ±5
x = −3 ± 5
Hringurinn sker x-ásinn í 2 og −8.
Á y-ásnum eru x-hnitin 0 þannig að við getum sett 0 inn í jöfnuna fyrir x til þess að finna hvar hringurinn sker y-ásinn.
(0 + 3)2 + y2 = 52
9 + y2 = 25
y2 = 25 − 9 = 16
y = ±4
Hringurinn sker y-ásinn í 4 og −4.

Við skulum nú teikna hring með miðju í (1, 1) og radíus 2 og nota til þess grafíska CASIO-reiknivél.
Við veljum fyrst CONICS í aðalvalmyndinni.

Síðan þurfum við að fletta niður yfir fjögur gröf og velja hringinn sem er fimmti möguleikinn í röðinni. Við flettum með ör niður (fjórum sinnum).
![]()
Þá sýnir skjárinn eftirfarandi:

Við veljum hring með miðju í (H, K) og radíus R með því að ýta á EXE og upp kemur eftirfarandi valmynd:

Nú sláum við inn H = 1, K = 1 og R = 2. Það er gert með eftirfarandi aðgerðaröð:
![]()
Niðurstaðan verður eftirfarandi graf:
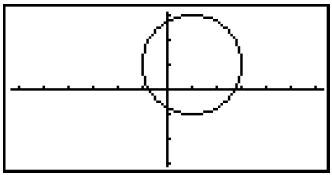
Við skulum nú skoða hvar línan y = x − 5 sker hringinn x2 − 6x + y2 − 4y = 3.
Athugum hvaða lausnir við fáum ef við setjum x − 5 í stað y í jöfnu hringsins.
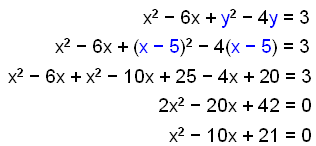 |
Deilum í gegn með 2. |
Hér þurfum við að nota lausnarformúluna þar sem
a = 1, b = −10 og c = 21
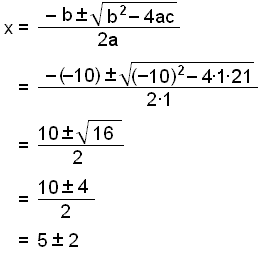
Lausnirnar eru x = 3 og x = 7.
Setjum þessar tölur inn í jöfnu línunnar og reiknum y.
y = x − 5 = 3 − 5 = −2 og y = x − 5 = 7 − 5 = 2
Skurðpunktarnir eru (3, −2) og (7, 2).
Við skulum að lokum teikna þetta upp í hnitakerfi.
Finnum þá tvo punkta sem eru í fjarlægðinni 10 frá punktunum (−3, −6) og (5, 10).
Þeir hljóta að vera skurðpunktar tveggja hringja með miðjur í (−3, −6) og (5, 10) og radíus 10 (sjá mynd).
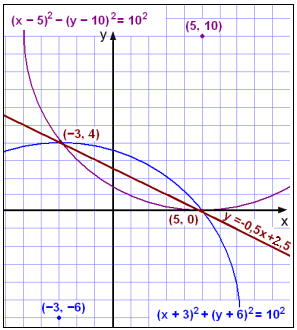
Jöfnur hringanna eru eftirfarandi:
(x + 3)2 + (y + 6)2 = 102 og (x − 5)2 + (y − 10)2 = 102
Við getum nú sett upp eftirfarandi jöfnu:
(x + 3)2 + (y + 6)2 = (x − 5)2 + (y − 10)2
Hún jafngildir því að segja, „fjarlægðin frá (−3, −6) í öðru veldi er jöfn fjarlægðinni frá (5, 10) einnig í öðru veldi."
|
Deilum í gegn með 16. |
Hér höfum við fengið línulegt samband á milli x og y, enda eru allir punktar sem eru í sömu fjarlægð frá tveimur punktum staðsettir á beinni línu sem er miðnormall línustriksins á milli punktanna. Skurðpunktar hringanna hljóta að vera á þessari línu sem við getum teiknað upp á forminu y = −½x + 2½ (sjá brúnu línuna á myndinni). Við skulum nú reikna út hvar línan sker hringana með því að setja x = (5 − 2y) í staðinn fyrir x í jöfnu annars hringsins.
(x + 3)2 + (y + 6)2 = 102
(5 − 2y + 3)2 + (y + 6)2 = 102
(8 − 2y)2 + (y + 6)2 = 100
64 − 32y + 4y2 + y2 + 12y + 36 = 100
5y2 − 20y = 0
5y(y − 4) = 0
Þessi jafna hefur lausnirnar y = 0 sem gefur x = 5 − 0 = 5 og y = 4 sem gefur
loks x = 5 − 2∙4 = −3. Skurðpunktarnir eru því (5, 0) og (−3, 4).
Æfðu þig á þessum aðferðum og taktu síðan próf
3 í reglu Pýþagórasar.
ps. mundu eftir að fylla út í tékklistann þinn jafnóðum