© 2007 Rasmus ehf og Jóhann Ísak
© 2007 Rasmus ehf og Jóhann Ísak |
Şríhyrningar |
|
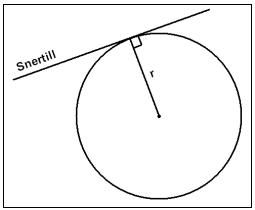
Lína sem snertir hring ağeins í einum punkti nefnist snertill. Snertill myndar ávalt 90° horn viğ radíus hringsins.
Lína sem skiptir horni í tvö jafn stór horn nefnist helmingalína. Á helmingalínu horns er sérhver punktur í sömu fjarlægğ frá báğum örmum hornsins. Hringur sem snertir sitt hvorn arminn hlıtur şví ağ hafa miğju á helmingalínunni.
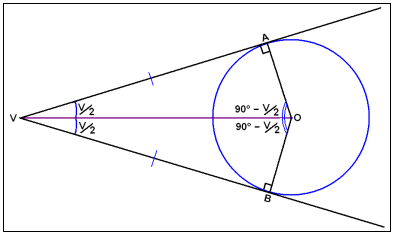
Á myndinni er lína gegnum V og O helmingalína hornsins V. Línustrikin VA og AB eru jafn löng og hornrétt á AO annars vegar og BO hins vegar.
Á eftirfarandi mynd er horniğ V = 40° og línustrikin VA og VB 40 cm. Finnum horniğ AOB og radíus hringsins.
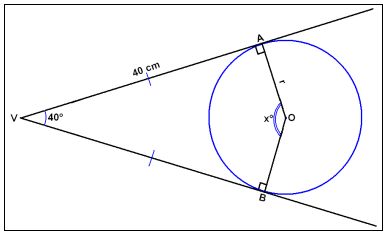
VAOB er ferhyrningur meğ hornasummuna 360° og şrjú şekkt horn. Şví gildir eftirfarandi:
x° = 360° − 90° − 40° − 90° = 140°
Ef viğ drögum helmingalínu 40° hornins frá V til O şá fáum viğ rétthyrndan şríhyrning meğ hornin 20°, 90° og 70°. Şá gildir eftirfarandi:
tan 20° = r/40
r = 40∙tan 20° ≈ 14,6 cm
Helmingalína horns í şríhyrningi skiptir mótlægri hliğ í sömu hlutföllum og eru á milli hliğanna sem liggja ağ horninu.
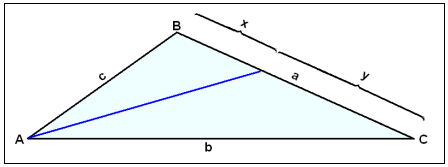
Helmingalína A skiptir hér hliğinni a í hlutföllunum c/b. Eftirfarandi gildir:
![]()
Hliğarnar í şríhyrningnum ABC eru eftirfarandi:
a = 30 cm, b = 40 cm og c = 20 cm.
Helmingalína hornsins A skiptir hliğinni a í tvo hluta. Reiknum lengd hlutanna.
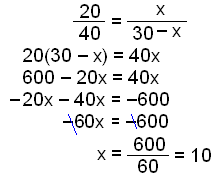
Hliğin a skiptist í 10 cm og 30 − 10 = 20 cm hluta.
Í öllum şríhyrningum getum viğ fundiğ einn punkt sem er í sömu fjarlægğ frá öllum hliğum hans. Í şessum punkti hljóta allar helmingalínur horna şríhyrningsins ağ skerast og şar er miğja hrings sem snertir allar hliğarnar. Slíkur hringur nefnist innritağur hringur.
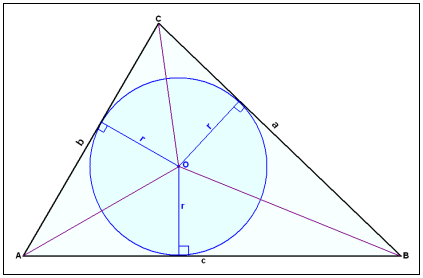
Viğ sjáum ağ helmingalínurnar AO, BO og CO skipta şríhyrningnum upp í şrjá minni şríhyrninga sem allir hafa hæğina r. Flatarmál şeirra er ½∙a∙r, ½∙b∙r og ½∙c∙r. Samanlagt flatarmál alls şríhyrnings verğur şá eftirfarandi:
F = ½∙a∙r + ½∙b∙r + ½∙c∙r = ½∙r(a + b + c)
Og şar sem ummál şríhyrningsins u er a + b + c verğur endanleg formúla svona:
![]()
Şağ er einnig til punktur innan eğa utan viğ şríhyrning sem er í sömu fjarlægğ frá öllum hornpunktum hans. Í umræddum punkti er miğja hrings sem sker alla hornpunkta şríhyrningsins. Hann nefnist umritağur hringur.
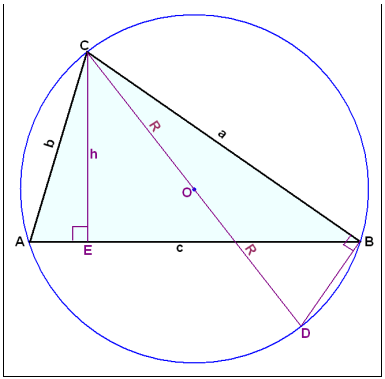
Myndin hér fyrir ofan sınir şríhyrninginn ABC meğ umrituğum hring. Einnig eru teiknağir tveir rétthyrndir şríhyrningar, ACE sem verğur til şegar hæğin h er dregin á grunnlínuna c og BCD sem verğur til şegar strengur er teiknağur frá C í gegnum miğpunkt hringsins ağ punktinum D á hringnum. Şríhyrningarnir ACE og BCD eru einslaga vegna şess ağ báğir eru rétthyrndir og auk şess spanna hornin A og D sama boga (bogann CB) og eru şví jafn stór. Viğ getum şví sett upp eftirfarandi umritun á hæğinni h:
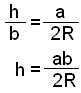
Ef viğ setjum şetta inn í formúluna fyrir flatarmáli şríhyrnings F = ½∙c∙h şá fáum viğ eftirfarandi formúlu:
![]()
Viğ hefğum einnig getağ sett şetta upp svona:
![]()
Út frá şessu fáum viğ eftirfarandi reglu:
![]()
Og ef viğ einöngrum h = b∙sin A og setjum inn í flatarmálsregluna F = ½∙c∙h şá fáum viğ eftirfarandi flatarmálsreglu:
F = ½∙b∙c∙sin A
Şríhyrningur hefur hliğarnar 17 cm, 17 cm og 16 cm.
a) Finnum flatarmáliğ.
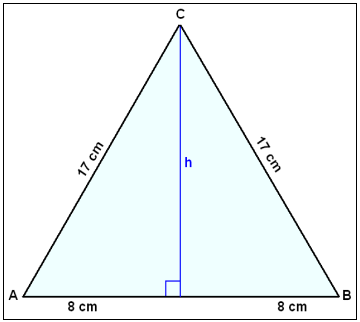
Notum Pışagórasarreglu til şess ağ finna hæğina h.
h2 + 82 = 172
h2 = 289 − 64 = 225
h = 15 cm
Nú getum viğ reiknağ flatarmáliğ
F = ½∙16∙15 = 120 cm2
b) Finnum nú radíus innritağs hrings.
Ummáliğ u = 17 + 17 + 16 = 50 cm.
F = 120 = ½∙r∙50
r =120∙2/50 = 4,8 cm
c) Şá skulum viğ næst finna radíus umritağs hrings.
F = 120 = 17∙17∙16/4R
480R = 17∙17∙16
R = 17∙17∙16/480 = 289/30 ≈ 9,6 cm
d) Finnum ağ lokum hornin í şríhyrningnum.
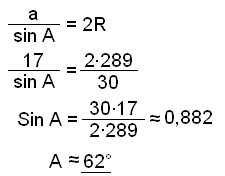
Şá er B ≈ 62° og C ≈ 180 − 2∙62 ≈ 56°.
Miğlínur í şríhyrningi eru línur frá hornpunkti ağ miğpunkti mótlægrar hliğar. Şær skerast allar í einum punkti og skurğpunkturinn skiptir miğlínunum í hlutföllunum 1: 2.
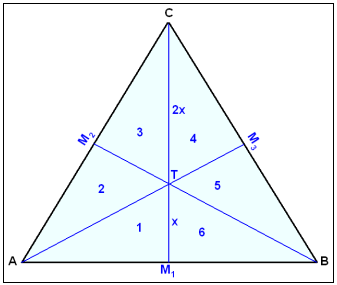
Á myndinni hér fyrir ofan eru M1, M2 og M3 miğpunktar hliğa şríhyrningsins. Miğlínurnar skerast í punktinum T sem skiptir M1C í hlutana x og 2x.
Miğlínurnar skipta şríhyrningi í sex minni şríhyrninga (1-6 á myndinni) sem allir hafa sama flatarmáliğ. Şetta hefur şağ í för meğ sér ağ T er şyngdarpunktur şríhyrningsins. Şríhyrningur úr einsleitu og jafn şykku efni á ağ geta haldiğ jafnvægi á blıantsoddi sem stungiğ er í şyngdarpunktinn.
Í jafnhliğa şríhyrningi er eru miğjur innritağs og umritağs hrings í sama punktinum. Miğlínurnar skerast í şessum punkti og sama gildir um hæğirnar á hliğarnar.
Miğlína í şríhyrningi er 24 cm löng. Reiknum í hve langa búta hinar miğlínurnar skipta henni.
x + 2x = 24
3x = 24
x = 8
Miğlínan skiptist í 8 cm og 16 cm hluta.
Şríhyrningur hefur hornpunktana A = (−4, −4), B = (12, 0) og C = (4, 16). Reiknum út skurğpunkt miğlínanna.
Viğ skulum byrja á şví ağ finna miğpunkt hliğarinnar a sem er meğaltal hnita B og C.
![]()
Finnum nú jöfnu miğlínunnar í gegnum A = (−4, −4) og (8, 8).
Hallatalan k = (8 + 4)/(8 + 4) = 1
Setjum şetta inn í skurğhallajöfnuna:
y = k(x − x1) + y1
y = 1(x − 8) + 8
y = x
Finnum næst miğpunkt hliğarinnar b sem er meğaltal hnita A og C.
![]()
Şá er næst ağ finna jöfnu línu í gegnum B og miğpunktinn á móti.
k = (0 − 6)/(12 − 6) = −½
y = −½(x − 0) + 6
y = −½x + 6
Leysum nú saman jöfnurnar y = x og y = −½x + 6.
x = −½x + 6
x + ½x = 6
1½x = 6
x = 4 og şar af leiğandi er y = 4
Skurğpunktur miğlínanna er (4, 4).
Sérstök regla gildir fyrir línur frá hornum şríhyrnings ağ einhverjum punkti (X, Y eğa Z) á mótlægri hliğ ef şær skerast allar şrjár í sama punktinum (P). Reglan er kennd viğ ítalska stærğfræğinginn Giovanni Ceva og er kölluğ Cevaregla.
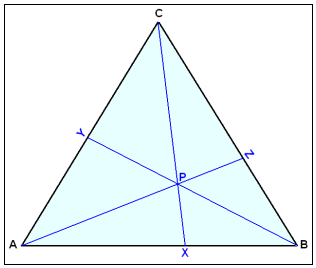
Reglan er eftirfarandi:
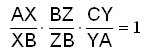
Reglan gildir einnig fyrir miğlínur og helmingalínur og raunar allar línur sem liggja frá hornum şríhyrnings og skerast í einum punkti og skipta mótlægu hliğunum.
Finnum í hve langa búta punkturinn Z skiptir hliğinni a (17 cm) í şríhyrningnum á myndinni hér fyrir neğan.
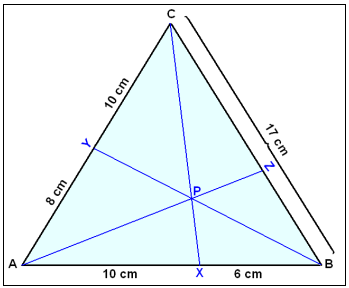
Viğ köllum x = BZ, en şá er ZC = 17 − x. Síğan setjum viğ beint inn í regluna:
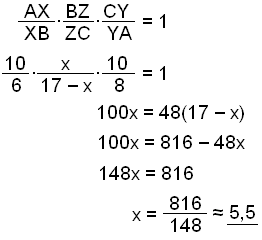
Şetta merkir ağ Z skiptir hliğinni í şví sem næst 5,5 cm og 11,5 cm búta.
Æfğu şig á şessum ağferğum og taktu síğan próf
2 í şríhyrningum.
ps. mundu eftir ağ fylla út í tékklistann şinn jafnóğum