Şríhyrningar
| © 2007 Rasmus ehf og Jóhann Ísak |
Şríhyrningar |
|
Kynning 3
Í kynningu 2 fundum viğ regluna
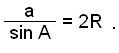
Şessa reglu getum viğ fullt eins vel leitt út frá horninu B og hliğinni b sem er mótlæg viğ şağ horn eğa út frá horninu C og mótlægu hliğinni c. Şetta gefur okkur eftirfarandi reglu, sem nefnd hefur veriğ sínusreglan:
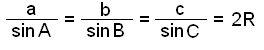 |
Şessa reglu má nota şegar horn og mótlæg hliğ í şríhyrningi eru şekkt auk einnar hliğar eğa horns til viğbótar. Ef eitthvağ şrennt er şekkt og horn ásamt mótlægri hliğ eru hluti af şví şá má finna meğ reglunni allar ağrar óşekktar hliğar og horn. Şetta er şví helsta grundvallarregla í landmælingum og kortagerğ. Henni má skipta upp í eftirfarandi şrjár reglur sem má nota til skiptis eftir şví hvağa horn og hliğar eru şekktar hverju sinni.
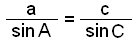 |
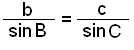 |
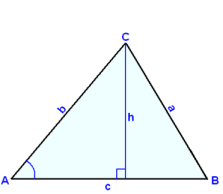
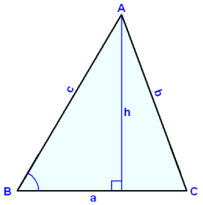
Á myndinni hér fyrir neğan stendur şríhyrningurinn á mismunandi hliğum líkt og honum hafi veriğ velt til hægri. Reiknum nú flatarmáliğ út frá horninu sem merkt er hverju sinni og ağlægum hliğum şess. Önnur ağlæga hliğin er şá grunnlína hverju sinni.
 |
 |
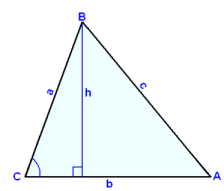 |
F = ½∙c∙h F = ½∙a∙h F = ½∙b∙h
Notum regluna sin x = mótlæg skammhliğ/langhliğ.
sin A = h/b sin B = h/c sin C = h/a
h = b∙sin A h = c∙sin B h = a∙sin C
Flatarmáliğ verğur şá eftirfarandi:
| F = ½ ∙c∙b∙sin A F = ½∙a∙c∙sin B F = ½∙b∙a∙sin C |
Şessar reglur má bæği nota til şess ağ reikna flatarmáliğ og til şess ağ leiğa út sínusregluna, en şağ er gert meğ şví ağ deila í gegn meğ ½∙a∙b∙c.
½∙b∙c∙sin A = ½∙a∙c∙sin B = ½∙a∙b∙sin C = F
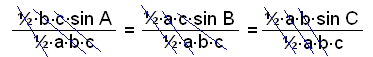
Şetta gefur eftirfarandi útlit á sinusreglunni:
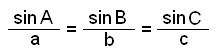 |
Sınidæmi 1
Í hvasshyrndum şríhyrningi er hliğin a = 12 cm, hliğin c = 13 cm og horniğ A = 60°. Finnum horniğ C, hliğina b og flatarmál şríhyrningsins.
Teiknum fyrst mynd til şess ağ átta okkur.
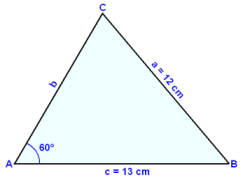
Byrjum á şví ağ setja upp sínusregluna og reikna horniğ C.
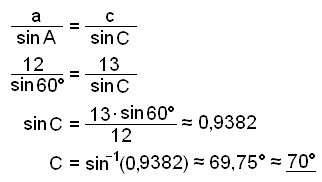
B ≈ 180° − 69,75° − 60° ≈ 50,25° ≈ 50°
Síğan setjum viğ upp regluna aftur til şess ağ reikna hliğina b.
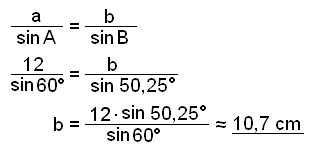
Loks notum viğ flatarmálsregluna og finnum flatarmáliğ.
F = ½∙b∙c∙sin A ≈ ½∙10,7∙13∙sin 60° ≈ 60 cm2
Sınidæmi 2
Í gleiğhyrndum şríhyrningi er hliğin a = 12 cm, hliğin c = 13 cm og horniğ A = 60°. Finnum horniğ C, hliğina b og flatarmál şríhyrninngsins.
Şetta er nákvæmlega sama dæmiğ og sınidæmi 1 ağ öğru leyti en şví ağ nú er şríhyrningurinn gleiğhyrndur şannig ağ eitt horniğ er meira en 90°.
Şegar viğ fundum horniğ C í sınidæmi 1 gerğum viğ ráğ fyrir ağ reiknivélin gæfi okkur rétta lausn enda var tekiğ fram ağ şríhyrningurinn væri hvasshyrndur. Útreikningarnir voru eftirfarandi:
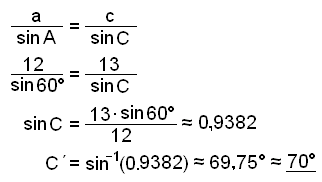 |
Şessi lausn gefur
ekki gleiğhyrndan şríhyrning.
Hins vegar eru tvær lausnir á jöfnunni: sinC = 0,9382 |
Rifjum upp regluna sem
gefur okkur hina lausnina. Hún er svona:
sin v° = sin (180° − v°)
Hin lausnin verğur samkvæmt
reglunni C ≈ 180° − 70°
≈ 110°
og horniğ sem eftir er verğur şá B ≈ 180° − 60° −
110° ≈ 10°
En hvağa skıring er á şví ağ mögulegar lausnir eru tvær ? Skoğum şağ á mynd.
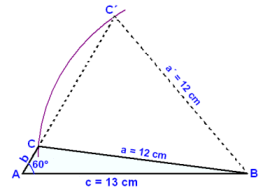
Viğ teiknum fyrst upp 13 cm grunnlínu og 60° horn viğ annan endann sem viğ köllum A. Hinn endann köllum viğ B. Şar stingum viğ niğur sirkli og teiknum hring meğ radíus 12 cm. Hann sker arm 60°hornsins A á tveimur stöğum og viğ veljum şann möguleika sem gefur gleiğhyrndan şríhyrning (sem er litağur á myndinni).
Setjum nú upp sinusregluna fyrir şennan şríhyrning og finnum hliğina b.
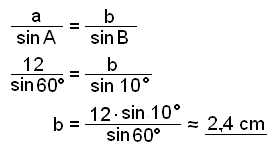
Şá eigum viğ bara eftir ağ reikna flatarmáliğ.
F = ½∙b∙c∙sin A ≈ ½∙2,4∙13∙sin 60° ≈ 13,5 cm2
Sınidæmi 3
Í gleiğhyrndum şríhyrningi er hliğin a = 15 cm, hliğin c = 6 cm og horniğ A = 60°. Finnum horniğ C og hliğina b.
Teiknum şríhyrninginn upp eins rétt og viğ getum.
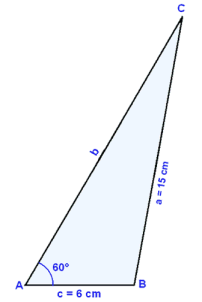
Setjum enn upp sinusregluna.
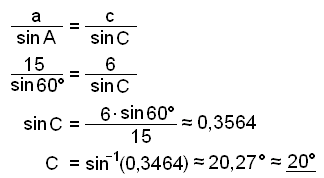
B ≈ 180° − 60° − 20,27° ≈ 99,73° ≈ 100°
Şá reiknum viğ næst út hliğina b.
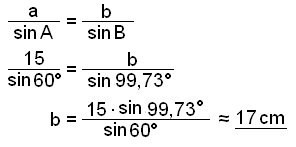
Şetta stenst samanburğ viğ teikninguna. Viğ şurfum şví ekki ağ hafa neinar áhyggjur. Şağ er ekki hægt ağ setja şennan şríhyrning saman á annan hátt.
Af sınidæmunum hér fyrir ofan og myndinni hér fyrir neğan getum viğ dregiğ eftirfarandi ályktun:
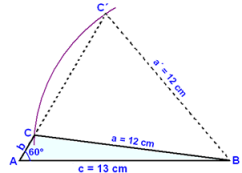
| Şegar mótlæg hliği viğ şekkt horn er styttri en ağlæga hliğin (grunnlínan) şá şurfum viğ aukaupplısingar um şağ hvort şríhyrningurinn er gleiğ- eğa hvasshyrndur eğa skila niğurstöğum í tvennu lagi. |
Sınidæmi 4
Í şríhyrningi er hliğin c = 12 cm og horniğ A = 60° og horniğ B = 80°. Finnum hliğarnar b og c.
Teiknum fyrst mynd. Viğ byrjum á şví ağ teikna 12 cm grunnlínu og reisum upp hornin. Hér eu öll hornin şekkt og ekki er hægt ağ teikna şríhyrninginn nema á einn veg. Viğ getum şví óhikağ notağ sínusregluna.
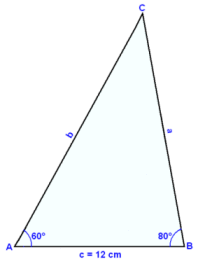
Nú vantar okkur mótlægt horn şannig ağ viğ byrjum á şví ağ reikna út horniğ C.
C = 180° − 60° − 80° = 40°
Nú getum viğ notağ sinusregluna til şess ağ finna hliğina a.
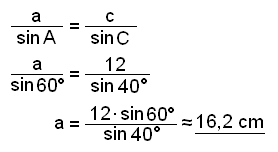
Loks finnum viğ hliğina b.
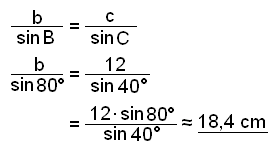
Viğ höfum nú séğ ağ sínusregluna má nota til şess ağ reikna út horn og hliğar í şríhyrningum şegar ein hliğ og tvö horn eru şekkt (sjá sınidæmi 4). Einnig höfum viğ komist ağ şví ağ sínusregluna má nota til şess ağ reikna horn og hliğar ef viğ şekkjum tvær hliğar og eitt mótlægt horn (sjá sınidæmi 1-3), en şá şurfum viğ stundum ağ vita hvort şríhyrningurinn er hvass- eğa gleiğhyrndur ef viğ ætlum ağ skila einni niğurstöğu. Ef upplısingarnar duga til şess ağ teikna şríhyrninginn nákvæmlega şá getum viğ reiknağ hann út.
Hvağ meğ şríhyrning şar sem tvær hliğar eru şekktar og horniğ á milli şeirra eğa şríhyrning şar sem allar hliğar eru şekktar en ekkert horn. Slíka şríhyrninga getum viğ teiknağ nákvæmlega og şağ ætti şví ağ vera mögulegt ağ reikna út horn og hliğar şeirra. En sínusreglan dugar ekki. Viğ verğum ağ reyna eitthvağ annağ.
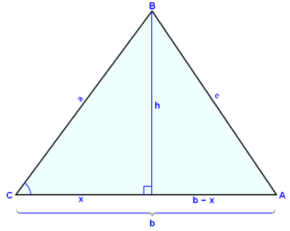
Setjum upp tvær formúlur yfir hæğina h meğ şví ağ nota reglu Pışagórasar.
h2 = a2 − x2 og h2 = c2 − (b − x)2 = c2 − b2 + 2∙b∙x − x2
Setjum şetta saman í eina reglu.
c2 − b2
+ 2∙b∙x − x2 = a2 − x2
Leysum şetta meğ tilliti til c2.
c2 = a2 + b2 − 2∙b∙x
Nú getum viğ losağ okkur viğ x-iğ í formúlunni meğ şví ağ nota okkur hornafallaregluna cos C = x/a sem viğ umritum á formiğ x = a cos C. Şetta setjum viğ inn í formúluna sem verğur şá eftirfarandi:
| c2 = a2 + b2 − 2∙b∙a∙cos |
Şessi formúla nefnist kósínusregla og hana má nota til şess ağ reikna út hliğina c ef hliğarnar a og b eru şekktar og horniğ C á milli şeirra (sjá myndina hér fyrir ofan).
Kósínusregluna má leiğa út á svipağan hátt fyrir gleiğhyrnda şríhyrninga og gildir jafnt fyrir şá og şar meğ alla şríhyrninga. Regluna má einnig leiğa út frá öğrum hornum og hliğum. Şannig fáum viğ eftirfarandi afbrigği:
| a2 = b2 +
c2 −
2∙b∙c∙cos
A
b2 = a2 + c2 − 2∙a∙c∙cos B |
Kósínusregluna má nota til şess ağ reikna út horn en şá şarf ağ leysa hana meğ tilliti til cos C og finna síğan horniğ í reiknivél. Skoğum şetta.
c2 = a2 + b2 − 2∙b∙a∙cos C
2∙b∙a∙cos C = a2 + b2 − c2
Ef viğ nú deilum í gegn meğ 2ab şá fáum viğ eftirfarandi reglu:
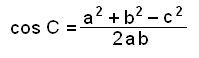 |
Viğ getum einnig leyst hin afbrigğin af kósínusreglunni á sama hátt, en şá fáum viğ eftirfarandi reglur:
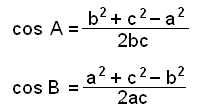 |
Sınidæmi 5
Í şríhyrningi er hliğin c = 12 cm og hliğin b = 15 cm. Horniğ A á milli hliğanna b og c er 60°. Finnum hliğina a, horniğ C og flatarmáliğ.
Teiknum fyrst mynd.
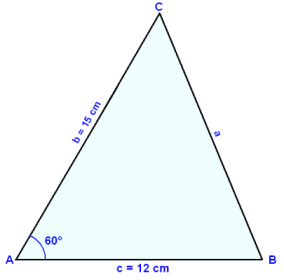
Notum afbrigğiğ meğ cos A.
a2 = b2 + c2 − 2∙b∙c∙cos A
= 152 + 122 − 2∙15∙12∙cos 60°
= 225 + 144 − 180 = 189
![]()
Nú getum viğ notağ sinusregluna til şess ağ finna horniğ C (viğ getum einnig notağ kósinusregluna).
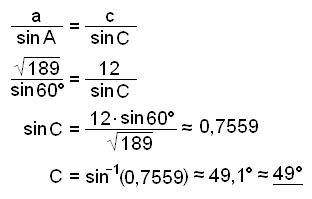
Şá er ağeins eftir ağ finna flatarmáliğ.
F = ½∙b∙c∙sin A ≈ ½∙15∙12∙sin 60° ≈ 78 cm2
Sınidæmi 6
Í şríhyrningi er hliğin a = 12 cm, hliğin b = 11 cm og hliğin c = 13 cm. Finnum flatarmáliğ.
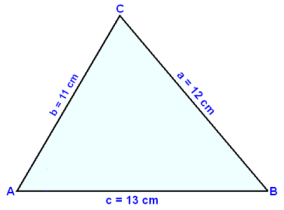
Til şess ağ reikna flatarmáliğ şurfum viğ ağ vita eitt horn. Viğ skulum şví reikna horniğ C meğ kósínusreglunni.
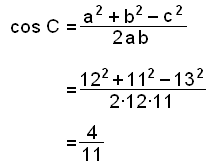 |
| C = cos-1(4/11) |
| C ≈ 68,7° |
Nú getum viğ reiknağ flatarmáliğ.
F = ½∙a∙b∙sin
C ≈ ½∙12∙11∙ sin 68,7° ≈ 61,5 cm2
Æfğu şig á şessum ağferğum og taktu síğan próf
3 í şríhyrningum.
ps. mundu eftir ağ fylla út í tékklistann şinn jafnóğum