© 2007  Rasmus ehf og Jóhann Ísak

Marghyrningar

Kynning 1 

Horn og flatarmál marghyrninga 

Við vitum að hornin í þríhyrningi eru samtals 180°. Þegar við hins vegar lítum til ferhyrnings þá getum við ekki umhugsunarlaust fullyrt að hornasumman sé 360°. Öllum ferningum má reyndar skipta upp í tvo þríhyrninga sem samtals eru 360°, en hér skiptir máli hvort hornin snúa út eða inn. 

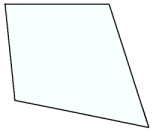
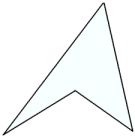
Úthyrndur ferhyrningur	Innhyrndur ferhyrningur

Við skulum nú skipta nokkrum úthyrndum marghyrningum upp í þríhyrninga og finna reglu til þess að reikna hornasummu þeirra.

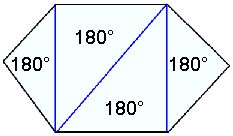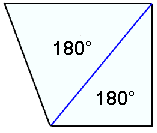
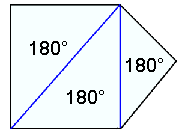
Ferhyrningur	Fimmhyrningur	Sexhyrningur

Ferhyrningurinn hefur hornasummuna  2∙180° = 360°, fimmhyrningur 3∙180° = 540°, sexhyrningur 4∙180° = 720° o.s.frv. Þannig er minnsti þríhyrningafjöldinn sem hægt er skipta marghyrningum upp í alltaf tveimur lægri en hornafjöldinn. Hornasumman er því 180° margfaldaðar með tölu sem er tveimur lægri en hornafjöldinn. Eftirfarandi formúla gildir því fyrir úthyrnda marghyrninga með n horn:

Hornasumma n-hyrnings = (n − 2)∙180°

Sýnidæmi 1

Finnum hornasummu sjöhyrnings.

Hornasumma = (7 − 2)∙180° = 5∙180° = 900°

Sýnidæmi 2

Finnum fjölda horna í marghyrningi sem hefur hornasummuna 1080°.

   (n − 2)∙180 = 1080

             n − 2 = 1080/180 = 6

                    n = 6 + 2 = 8

Þetta er átthyrningur.

Flatarmál n-hyrninga má oft finna með því að skipta þeim upp í þríhyrninga. Flatarmál þríhyrninganna er reiknað og síðan er lagt saman.

Sýnidæmi 3

Fimmhyrningnum hér fyrir neðan hefur verið skipt upp í þrjá þríhyrninga.

a)  Finnum hornin D og B.

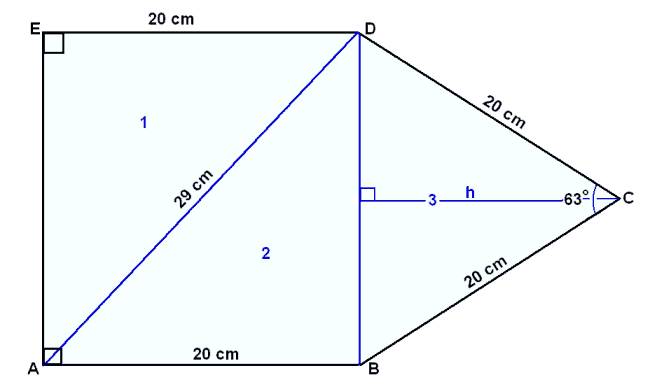
Þríhyrningur 3 (BCD) er jafnarma þannig að hornin BDC og CBD eru jafn stór. Köllum þau x. Við þau bæði bætast 90° þannig að hornin B og D eru bæði jafn stór eða 90° + x. Þá gildir eftirfarandi:

       360° + 2x + 63° = 540°

                            2x = 540° − 360° − 63° = 117°

                              x = 117/ 2 = 58,5°

Hornin B og D eru því hvort um sig 58,5° + 90° = 148,5°

b)  Finnum flatarmál fimmhyrningsins.

    Byrjum á því að finna hliðina AE sem er jafn löng hornalínunni BD. Köllum hana x.

Þríhyrningur 1 hefur því flatarmálið

   F₁ = ½∙20∙21 = 210 cm²                    F = ½∙g∙h

Þríhyrningur 2 er eins og hefur þetta sama flatarmál.

Reiknum næst hæðina h í þríhyrningi 3 frá C niður á BD.

Hæðin myndar rétthyrndan þríhyrning með langhliðina 20 cm og skammhlið sem er 21/2 = 10,5 cm.

F₃ ≈ ½∙21∙17 ≈ 178,5 cm ²

F = F₁ + F₂ + F₃ ≈ 210 + 210 + 178,5 ≈ 600 cm ²

Reglulegir kallast þeir marghyrningar sem eru með öll hornin jafn stór og allar hliðar jafnlangar.

Einnig hafa innritaður og umritaður hringur sömu miðju og marghyrningurinn.

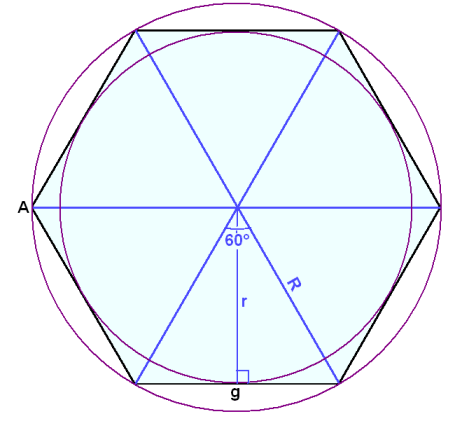
Við getum skipt reglulegum marghyrningum upp í jafn marga miðjuþríhyrninga og fjöldi horna segir til um (eða n þríhyrninga í n-hyrningi) eins og myndin sýnir. Hver þríhyrningur er jafnarma með hliðarlengd sem er jöfn radíus umritaðs hrings R og hæð sem er jöfn radíus innritaðs hrings r. Topphornið verður 360°/n, enda skipta n þríhyrningar með sér heilum hring við miðpunktinn. Í 6-hyrningi verður þetta horn 360°/ 6 = 60°. Hin hornin í þríhyrningunum eru fundin með því að draga topphornið frá 180° og deila með tveimur. Ef við viljum hins vegar finna hve stórt hvert horn í marghyrningnum er þá dugir að draga topphornið frá 180° vegna þess að radíus umritaðs hrings sem dregin er frá einhverju horni er helmingalína þess horns.

Formúla fyrir stærð horns í reglulegum n-hyrningi verður eftirfarandi:

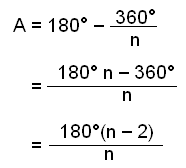
Þetta er í raun formúlan fyrir hornasummu n-hyrnings deilt með n sem er fjöldi horna.

Við sjáum að flatarmál hvers miðjuþríhyrnings verður ½∙r∙g þar sem g er lengd hliða í marghyrningnum. Flatarmál marghyrningsins verður því ½∙r∙g∙n.

 Þar sem g∙n er í raun ummál marghyrningsins sem við getum kallað u þá má umrita formúluna svona:

F = ½∙r∙u

Það er áhugavert að skoða flatarmál hrings í þessu ljósi. Við getum litið á hring sem reglulegan marghyrning með óendanlega mörgum hornum. Slíkur marghyrningur fellur í raun saman við innritaða hringinn. Nú er p hlutfallið á milli ummáls hrings (u) og þvermáls (2r). Því er u = 2pr og ef við setjum þetta inn í jöfnuna hér fyrir ofan þá fáum við

                F = ½∙r∙u = ½∙r∙2pr = r² p

Sýnidæmi 4

Ummál 5-hyrnings er 50 cm. Finnum flatarmálið og radíus umritaðs hrings.

Fyrst þurfum við að skipta 5-hyrningnum í miðjuþríhyrninga og finna þau horn sem um ræðir.

    Hornasumman í 5-hyrningi er (5 − 2)∙180° = 540°

    Hvert horn er þá 540°/5 = 108° og helmingurinn af því er 54°.

    Hornin við miðpunktinn eru 360°/5 = 72° og helmingurinn af því er 36°.

    Síðan er hver hlið 50/5 = 10 cm.

Við skulum nú teikna upp mynd og setja inn á hana þessar upplýsingar til þess að átta okkur betur á dæminu.

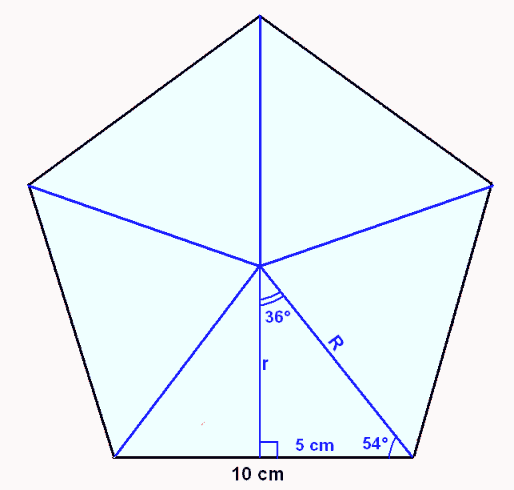
Nú getum við notað hornafallareglurnar:

   F = ½∙r∙u ≈ ½∙6,9∙50 ≈ 172 cm²

Reiknum nú R.

Sýnidæmi 5

Hornalína í 8-hyrningi er 20 cm löng. Finnum radíus innritaðs hrings og flatarmálið.

   Hér er hornasumman (8 − 2)∙180° = 1080°.

   Hvert horn er því 1080/8 = 135° og helmingurinn af því er 135/2 = 67,5°.

   Hornin við miðpunktinn eru 360°/ 8 = 45° og helmingurinn af því er 22,5°.

Við skulum nú teikna upp mynd og setja inn á hana þessar upplýsingar til þess að átta okkur betur á dæminu.

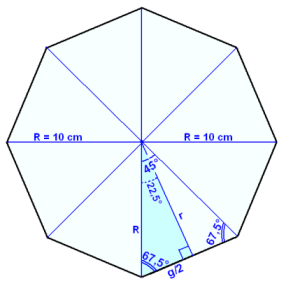
Við höfum nú þríhyrning með langhliðina R = 10 cm og horn sem eru 90°, 67,5° og 22,5°.  

Nú notum við hornaföllin.

Reiknum nú hliðarlengdina.

Nú getum við reiknað ummálið með því að margfalda hliðarlengdina með 8 og síðan flatarmálið.

   u ≈ 8∙7,6537 ≈ 61,2293 cm

   F = ½∙r∙u ≈ ½∙9,2388∙61,2293 ≈ 283 cm²

Æfðu þig á þessum aðferðum og taktu síðan próf 1  í  Marghyrningum.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum