© 2007  Rasmus ehf    og Jóhann Ísak

Hornareglur

Kynning 1    Pýþagórasarreglan fyrir kósínus og sínus

Stærðfræðingar hafa búið til mikið regluverk til þess að einfalda og umrita stæður með hornaföllum og til þess að leysa flóknar hornafallajöfnur. Við skulum líta á eina af þessum reglum og nota hana lítið eitt.

Þessi regla hefur verið nefnd hornafallaeining eða Pýþagórasarregla fyrir kósínus og sínus. Ef við skoðum þríhyrninginn hér til hliðar sjáum við að samkvæmt reglu Pýþagórasar þá gildir eftirfarandi regla hvaða stöðu sem punkturinn P kann að taka á hringnum.

 
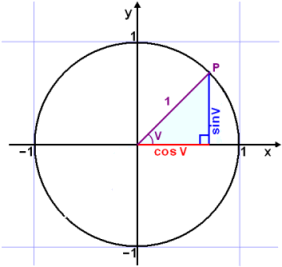sin 2 v + cos 2 v = 1

Þessa reglu getum við síðan umritað á eftirfarandi tvo vegu:  

sin 2 v = 1 − cos 2 v

og

cos 2 v = 1 - sin 2 v

Sýnidæmi 1

Finnum sin x ef cos x = ⅓ og 0 x < /2 (x er á bilinu 0° til 90°).

Nú getum við gert þetta í reiknivél með því að reikna cos−1 (⅓) ≈ 70,53° og sin 70,53° ≈ 0,94. Við skulum hins vegar reikna þetta með Pýþagórasarreglunni og fá út nákvæma niðurstöðu.

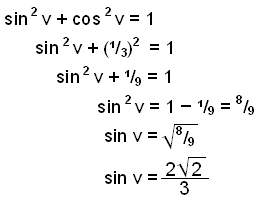
Sýnidæmi 2

Notum regluna sin2 v + cos2 v = 1 til þess að umrita stæðuna 1/ cos 2 v.

Við sjáum strax að við getum umritað regluna með því að færa sin2 v yfir jafnaðarmerkið. Þá fáum við regluna cos2 v = 1 − sin2 v sem við getum sett beint inn.

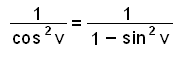
En það er einnig til önnur umritun sem e.t.v. liggur ekki eins beint við. Athugum hvað kemur út ef við setjum  sin2 v + cos2 v inn fyrir ofan strikið í stað eins.

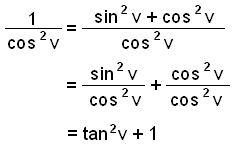
Við höfum nú leitt út eftirfarandi reglu:

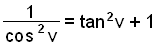
Sýnidæmi 3

Við skulum nú nota reglu Pýþagórasar fyrir kósínus og sínus til þess að umrita jöfnuna sin2 v = cos2 v, annars vegar yfir á formið sin2 v = ½ og hins vegar yfir á formið cos2 v = ½.

Við notum fyrst umritunina cos2 v = 1 − sin2 v.

      sin2 v = cos2 v

      sin2 v = 1 − sin2 v

   2∙sin2 v = 1

      sin2 v = ½

Nú notum við sin2 v = 1 − cos2 v.

          sin2 v = cos2 v

   1 − cos2 v = cos2 v

                 1 = 2∙cos2 v

         cos2 v = ½

Sýnidæmi 4

Leysum jöfnuna cos2 x = sin x + 1

        cos2 x = sin x + 1

   1 − sin2 x = sin x + 1

                0 = sin2 x + sin x = sin x (sin x + 1)

Nú er annað hvort sin x = 0 eða sin x = −1.

Þá er x = k∙ (k∙180°) eða x = 3/2 + k∙2 (270° + k∙360°).

Sýnidæmi 5

Einföldum jöfnuna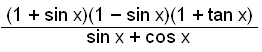

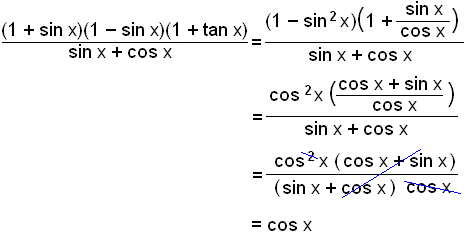Hér notum við regluna

(a + b)(a − b) = a2 − b2

og síðan leysum við tan upp í  sin/cos og setjum á eitt strik..

 

Æfðu þig á þessum aðferðum og taktu síðan próf 1 í hornareglum.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum