© 2007  Rasmus ehf    og Jóhann Ísak

Hornareglur

Kynning 2  

Samlagningarreglur, frádráttarreglur og reglur fyrir tvöfalt horn

Reglur fyrir hornaföll tveggja samanlagðra horna og mismun tveggja horna eru talsvert gagnlegar. Við skulum nú búa okkur til slíkar reglur.

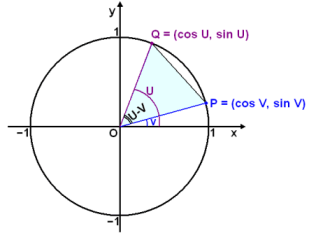
Þríhyrningurinn OPQ á myndinni er með hornpunktana P og Q á einingarhring en O er miðja hnitakerfisins. Hornið á milli x-ássins og OQ köllum við u og hornið á milli OP og x-ássins köllum við v. Hornið POQ er því u − v. Punkturinn Q hefur hnitin (cos u, sin u) og punkturinn P hnitin (cos v, sin v). Fjarlægðina á milli P og Q köllum við |PQ| og við skulum nú reikna þessa fjarlægð með fjarlægðarformúlunni.

   |PQ|2 = (cos u − cos v)2 + (sin u − sin v)2  

            = cos2u − 2 cos u cos v + cos2v

               + sin2u − 2 sin u sin v + sin2v  

            = 1 − 2 cos u cos v− 2 sin u sin v + 1

            = 2 − 2 cos u cos v − 2 sin u sin v

 Við margföldum 
(fjarlægð)2 =
(x2−x1)2 + (y2−y1)2

 

 

 

Við skulum einnig reikna þetta með kósínusreglunni.

   |PQ|2 = 12 + 12 − 2∙1∙1∙cos (u − v)

             = 2 − 2∙cos (u − v)

Nú getum við sett þetta tvennt saman.

   2 − 2∙cos (u − v) = 2 − 2 cos u cos v − 2 sin u sin v

      − 2∙cos (u − v) = − 2 cos u cos v − 2 sin u sin v

Ef við nú deilum í gegn með −2 fáum við eftirfarandi reglu:

cos (u − v) = cos u cos v + sin u sin v

Ef við nú setum inn −v inn fyrir v fáum við eftirfarandi:

   cos (u − (−v)) = cos u cos (−v) + sin u sin (−v)

Nú getum við lesið af einingarhringnum að cos (−v) = cos v og sin (−v) = − sin v. Ef við notum þetta til þess að umrita stæðuna hér fyrir ofan þá fáum við eftirfarandi reglu:

cos (u + v) = cos u cos v − sin u sin v

Við margföldum upp úr svigunum og einföldum

Á myndinni hér fyrir neðan eru tveir þríhyrningar. Annar myndar hornið v frá x-ásnum en hinn frá y-ásnum þannig að þeir eru einslaga.

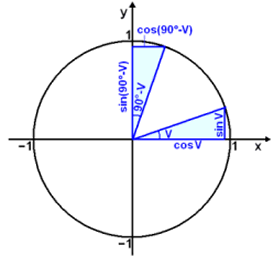
Einslaga þríhyrningarnir gefa okkur eftirfarandi reglur:

   cos v  = sin (90° − v)    og   sin v = cos (90° − v)

Við skulum nú setja 90° í stað u og (u + v) í stað v í þessum reglum. 

    sin (u + v) = cos (90° − (u + v))

                     = cos ((90° − u) − v)

                     = cos (90° − u) cos v + sin (90° − u) sin v

                     = sin u cos v + cos u sin v

Með þessu höfum við fundið eftirfarandi reglu fyrir sin (u + v):

sin (u+v) = sin u cos v + cos u sin v

Ef við nú setjum (−v) í stað v í þessari reglu fáum við eftirfarandi:

sin (u − v) = sin (u + (−v))

                    = sin u cos (−v) + cos u sin (−v)

                    = sin u cos v − cos u sin v

 Við notum regluna

cos(u−v) = cos u cos v−sin u sinv og síðan sin v = cos (90° − v)

og cos v  = sin (90° − v).

Þar með höfum við fengið eftirfarandi reglu fyrir sin (u − v):

sin (u-v) = sin u cos v - cos u sin v

 

Ef við yfirfærum reglurnar fyrir sin (u + v) og cos (u + v) á sin (u + u) og cos (u + u) fáum við eftirfarandi reglur:

sin 2u = 2 sin u cos u

cos 2u = cos2 u − sin2

Seinni regluna getum við umritað á tvo vegu með reglunni     cos2 u + sin2 u = 1. 

Formin cos2 u = 1 − sin2 u og sin2 u = 1 − cos2 u eru þá sett inn fyrir sin2 u og cos2 u. Þá fást eftirfarandi reglur:

cos 2u = 2 cos2 u − 1

cos 2u = 1 − 2 sin2 u

Sýnidæmi 1

Reiknum út nákvæm gildi á sin 15° og cos 15°.

Við höfum áður reiknað út að cos 45° = 2/2, sin 45° = 2/2, cos 60° = ½ og sin 60° = 3/2.
Samkvæmt reglunni um cos af mismuni horna gildir eftirfarandi:

   cos 15° = cos (60° − 45°)

                 = cos 60° cos 45° + sin 60° sin 45°

                 = ½∙2/2 + 3/2∙2/2

                 = 2/4 + 3∙2/4

                 = 2∙(1 + 3)/4

Samkvæmt reglunni um sinus af mismuni horna gildir eftirfarandi:

     sin 15° = sin (60° − 45°)

                 = sin 60° cos 45° − cos 60° sin 45°

                 = 3/2∙2/2 − ½∙2/2

                 = 3∙2/4 − 2/4

                 = 2∙(3 − 1)/4

Sýnidæmi 2

Einföldum stæðuna sin (270° − v).

Notum regluna sin (u − v) = sin u cos v − cos u sin v.

sin (270° − v) = sin 270° cos v − cos 270° sin v

                       = −1∙ cos v − 0∙ sin v         

                       = − cos v

sin 270° = −1

 cos 270° = 0

Sýnidæmi 3

Finnum reglu fyrir cos 3x sem inniheldur aðeins sin x og cos x.

Við notum regluna cos (u + v) = cos u cos v − sin u sin v og setjum 2x inn fyrir u og x inn fyrir v.

cos (2x + x) = cos 2x cos x − sin 2x sin x cos 2x = cos2x − sin2x       sin 2x = 2 sin x cos x

                           = (cos2 x − sin2 x)∙cos x − (2 sin x cos x)∙sin x

                      = cos3 x − sin2 x cos x − 2 sin2 x cos x

                      = cos3 x − 3 sin2 x cos x

Sýnidæmi 4

Leysum jöfnuna sin 2x + 2 sin x = 0 á bilinu 0 x < 2p.

              sin 2x + 2 sin x = 0

   2 sin x cos  x + 2 sin x = 0

         2 sin x (cos  x + 1) = 0

 

Við notum regluna
sin 2x = 2 sin x cos x

 

Jafnan hefur lausnir þar sem sin x = 0 og cos x = − 1.

   sin x = 0

         x = 0 eða (0° eða 180°)

   cos x = −1

          x = (180°)

Lausnirnar eru 0 og .   

Sýnidæmi 5

Leysum jöfnuna 7 cos2 x + 5 sin2 x + 6 sin 2x = 0

Við byrjum á því að nota regluna sin 2x = 2 sin x cos x.

   7 cos2 x + 5 sin2 x + 12 sin x cos x = 0

Oft er gott að deila í gegn með kósínus í réttu veldi þegar leysa á jöfnur með blöndu af sin og cos.
Með því má oft fá leysanlega tan-jöfnu.

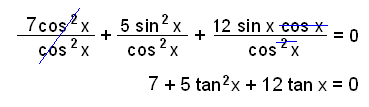
Þetta er annars stigs jafna með a = 5, b = 12 og c = 7.

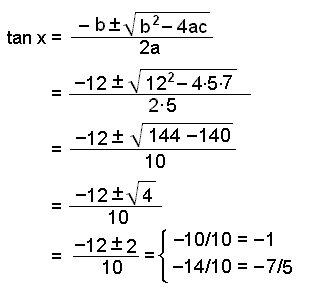
   tan x = −1 gefur x = −/4 + k∙  (−45° + k∙180°)

   tan x = −7/5 gefur hins vegar ekkert heilt margfeldi af en

         x ≈ −0,95 + k∙  (54,5° + k∙180°)

Æfðu þig á þessum aðferðum og taktu síðan próf 2 í hornareglum.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum