© 2007  Rasmus ehf    og Jóhann Ísak

Hornareglur

Kynning 3     Jöfnur af gerðinni  a sin x + b cos x = c

Skoðum graf fallsins f(x) = sin x + 2 cos x.

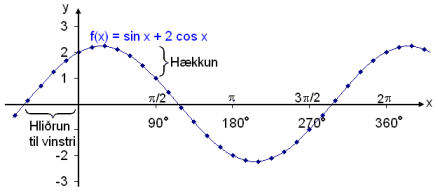
Okkur til furðu þá kemur út regluleg sínuskúrfa. Reyndar er hún með hærra útslag en einföld sínuskúrfa og hliðruð til vinstri. Við höfum áður (sjá hornaföll, kynning 3) skoðað hvernig hækka má útslag sínuskúrfuna með því að margfalda hana með fastri tölu stærri en 1. Við höfum einnig séð hvernig hliðra má kúrfunni til vinstri með því að bæta við horni. Við ættum því að geta sett upp eftirfarandi jöfnu:

   m sin (x + v) = sin x + 2 cos x

Skoðum næst graf fallsins g(x) = sin x − 2 cos x.

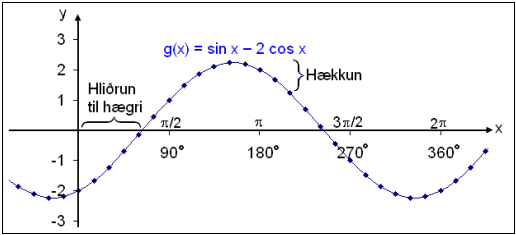
Þetta er greinilega sama sínuskúrfan með hækkað útslag en nú er hún jafn mikið hliðruð til hægri eins og hin fyrri var hliðruð til vinstri. Við getum því aftur sett upp samsvarandi jöfnu.

   m sin (x − v) = sin x − 2 cos x

Við getum umritað þessar jöfnur með reglum um summu og mismun horna (sjá kynningu 2), en þær eru eftirfarandi:

   sin (x + v) = sin x cos v + cos x sin v

   sin (x − v) = sin x cos v − cos x sin v

Margföldum nú í gegn með m.

   m sin (x + v) = m sin x cos v + m cos x sin v

   m sin (x − v) = m sin x cos v − m cos x sin v

Berum þetta nú saman við upphaflegu jöfnurnar.

   m sin (x + v) =      1 sin x       + 2 cos x

                        = m cos v sin x + m sin v cos x

   m sin (x − v) =      1 sin x         − 2 cos x

                        = m cos v sin x  − m sin v cos x

Við sjáum að í báðum tilfellum hlýtur eftirfarandi að gilda:

   m cos v = 1

    m sin v = 2

Ef við nú deilum neðri jöfnunni með þeirri efri fáum við eftirfarandi:

   tan v = ²/₁

Þetta gefur okkur hornið v = tan⁻¹ (2) ≈ 63,4°.

Við skulum nú teikna upp rétthyrndan þríhyrning með skammhliðarnar 1 og 2 eins og stuðlarnir eru í jöfnunni.

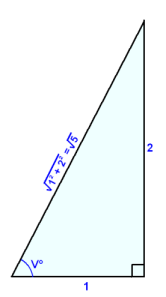
Við sjáum af þríhyrningnum að

   cos v = 1/ og sin v = 2/.

Einnig höfum við jöfnurnar

   m cos v = 1

    m sin v = 2.

Þetta gefur okkur eftirfarandi:

   m∙1/ = 1

           m =

Við getum sem sagt umritað jöfnurnar á eftirfarandi hátt:

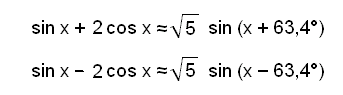
Nú sjáum við að útslag bylgnanna f(x) = sin x + 2 cos x og g(x) = sin x − 2 cos x er .

Ef við reiknum þetta með stuðlunum a og b þá fáum við eftirfarandi reglur sem gilda almennt:

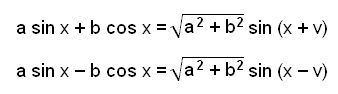Hornið v getum við síðan fundið út frá eftirfarandi reglu:

Sýnidæmi 1

Finnum mesta útslag bylgjunnar f(x) = 3 sin x + 4 cos x.

Við byrjum á því að umrita fallið.

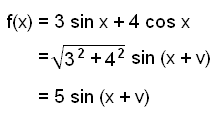
Útslagið er 5.

Sýnidæmi 2

Graf fallsins f(x) = 3 sin x + 4 cos x er hliðruð sínusbylgja.

Skoðum hvernig hún hefur hliðrast.

   f(x) = 3 sin x + 4 cos x

         = 5 sin (x + v)

      v = tan ⁻¹ (4/3) ≈ 53,1°

Bylgjan hefur hliðrast 53,1° til vinstri (f(x) ≈ 5 sin (x + 53,1°).

Sýnidæmi 3

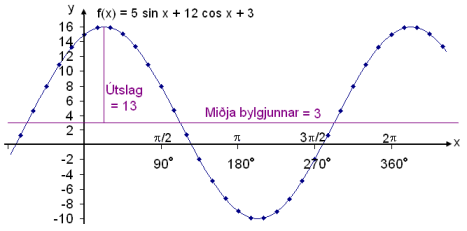
Skoðum graf fallsins f(x) = 5 sin x + 12 cos x + 3. Finnum útslagið og hve mikilli hæð frá x-ásnum bylgjutopparnir ná.

Umritum f(x).

   tan ⁻¹ (12/5) ≈ 67,4°

   f(x) = 13 sin (x + 67,4°) + 3

Útslagið er 13 og mesta hæðin verður 13 + 3 = 16. Lítum loks á grafið.

Sýnidæmi 4

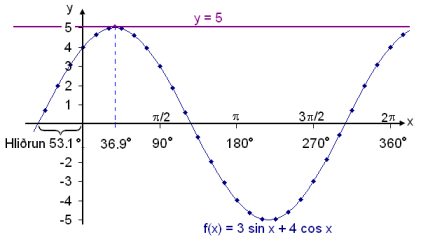
Leysum jöfnuna 3 sin x + 4 cos x = 5 á bilinu 0° x < 360°.

   3 sin x + 4 cos x = 5

                              = 5 sin (x + 53,1°)

      sin (x + 53,1°) = 5/5 = 1

              x + 53,1° = sin ⁻¹ 1 = 90° + k∙360°

                            x = −53,1° + 90° + k∙360°

                            x = 36,9°

Þetta gefur aðeins lausnina 36,9° á fyrsta hring.

Við skulum að lokum  skoða grafið okkur til fróðleiks.

Sýnidæmi 5

Finnum allar lausnir á jöfnunni sin x − cos x = 1.

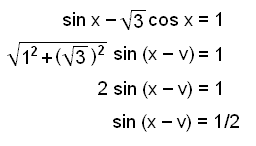
Nú er tan v = og v = tan () ⁻¹ = ^p/₃ (60°).

   sin (x − /₃) = ½

(x − /3) = sin −1 (½) = /6 + k∙2

/6 = 30°

                    x = /₃ + /₆ + k∙2

                       = /₂ + k∙2

eða

         (x − /₃) = − /₆ + k∙2

                     x = /₃ + − /₆ + k∙2

x = 7/6 + k∙2p

7/6 = 210°

Æfðu þig á þessum aðferðum og taktu síðan próf 3 í hornareglum.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum