© 2007  Rasmus ehf    og Jóhann Ísak

Vigrar

Kynning 2  

Liðun vigra

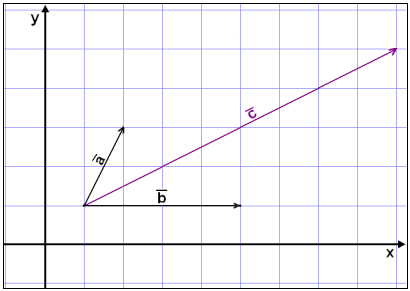
Þegar vigrinum er skipt upp í tvo aðra vigra og þannig  að + = þá kallast það að liða vigurinn  (sjá myndina fyrir neðan).

Oft eru er vigrum skipt upp í lóðrétta og lárétta liði eins og sýnt er hér til hliðar, enda er það mikilvægt t.d. í kraftafræði. Eigi að síður þurfum við að geta skipt upp í liði samsíða tveimur öðrum vigrum sem geta haft hvaða stefnu sem er. Við skulum skoða kunnuglegt dæmi um það hvernig við getum tjáð vigurinn á myndinni hér fyrir neðan með og , en það er í raun liðun á vigrinum samsíða og .

Bætum nú öðrum vigri við þann sem fyrir er og síðan einum og hálfum .

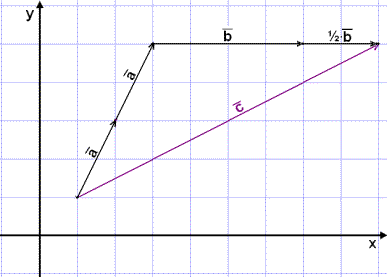
Við sjáum að liðirnir eru 2 og 1½. Við getum liðað sérhvern vigur í þætti samsíða einhverjum tveimur vigrum og ef enginn vigranna hefur lengdina 0 (sem kallast núllvigur). Þetta getum við gert með því að finna tölurnar t og r þannig að eftirfarandi gildi:

   = r∙+ t∙

Galdurinn er fólginn í því að finna tölur t og r þannig að jafnan verði sönn.

Sýnidæmi 1

Við skulum nú liða vigrana , og á myndunum hér fyrir ofan í lárétta og lóðrétta liði. Við skulum nota láréttan vigur með lengdina 1 (ein rúða) og jafn langan lóðréttan vigur. Slíkir vigrar eru kallaðir einingarvigrar og jafnan táknaðir
og .

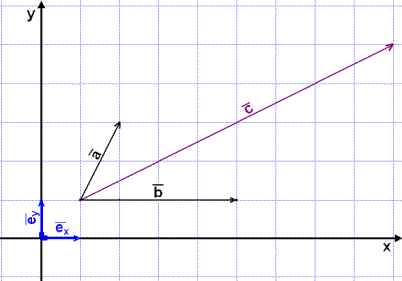
Byrjum á því að liða .

Ljóst er af myndinni að = + 2.

Við getum einfaldlega talið þetta út. Vigurinn telst vera fjórar einingar til hægri og engin upp, en vigurinn átta til hægri og fjórar upp.

= 4 og = 8 + 4.

Sýnidæmi 2

Kraftur er 100 N og verkar 25° á ská upp. Hve mikið verkar hann beint áfram og beint upp?

Teiknum þetta til þess að átta okkur á aðstæðum.

Nú getum við notað hornareglurnar til þess að reikna || og ||

Láréttur liður eins og við fundum í dæminu hér fyrir ofan (liðurinn ) kallast ofanvarp vigursins á x-ásinn. Einnig má tala um vörpun  á y-ásinn. Við skulum skoða þetta á mynd.

Á að vera a sin v° lóðrétt.

Á þennan hátt getum við einnig fundið ofanvarp á láréttar línur og lárétta vigra. Formúlurnar eru eftirfarandi:

Ofanvarp  á x-ás = ||∙cos v° Vörpun á y-ás = ||∙sin v°

 

---

Sýnidæmi 3

Vigurinn hefur lengdina 3 og stefnir 20° frá láréttu, vigurinn hefur lengdina 4 og stefnir 40° frá láréttu og vigurinn hefur lengdina 5 og stefnir 70° frá láréttu. Stefnurnar gefa að hornið á milli og er 20° og hornið á milli og er 30°. Við skulum nú skipta vigrinum í liði samsíða og , en byrjum á því að teikna þetta upp. Fljótt á litið virðist þetta ekki árennilegt verkefni en ef við teiknum upp liðunina þá skýrist þetta.

Við þurfum að finna vigrana r∙ og t∙ sem samanlagt mynda vigurinn . Þegar við teiknum upp samlagningu vigranna kemur fram þríhyrningur (blár á myndinni) sem hefur 30° (hornið á milli og ) og 20° horn (hornið á milli  og ) þannig að þriðja hornið hlýtur að vera 180°− 30°− 20° = 130°. Með öðrum orðum, við þekkjum öll hornin í þríhyrningnum og eina hlið sem er 4 á lengd (||= 4). Það gefur okkur færi á að nota sinusregluna.

Hér notum við sínusregluna og margföldum í gegn með sin 30°.

Á sama hátt finnum við t∙||

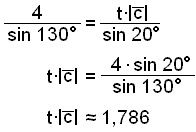
Við höfum nú fundið lengdir hliða þríhyrningsins. Nú þurfum við að finna tölurnar r og t. Byrjum á r.

   r∙|| ≈ 2,611

      r∙3 ≈ 2,611

         r ≈ 2,611/3 ≈ 0,87

Reiknum síðan t.

    t∙|| ≈ 1,786

      t∙5 ≈ 1,786

         t ≈ 1,786/5 ≈ 0,36

Endanlega verður liðunin þá eftirfarandi:

   ≈ 0,87∙ + 0,36∙

Við sjáum það af sýnidæminu hér fyrir ofan (sýnidæmi 3) að við getum notað sínusregluna til þess að skipta vigri í liði samsíða tveimur öðrum vigrum. Við þurfum ekki að þekkja meira en stefnur vigranna þriggja og lengd vigursins sem þarf að liða. Þetta er mjög gagnleg aðferð þannig að við skulum ramma hana inn.

Þegar við vinnum með vigra í hnitakerfi verður liðun þeirra mun einfaldari. Í sýnidæmi 1 kynntum við til sögunnar lárétta og lóðrétta vigra og , en þeir hafa lengd sem samsvarar einni einingu hnitakerfisins og kallast einingarvigrar.

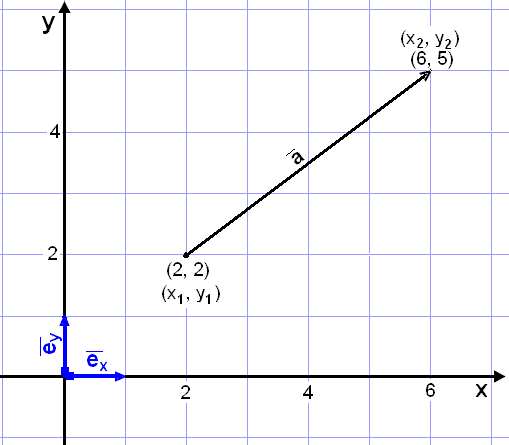
Við getum liðað vigurinn á myndinni hér fyrir ofan á sama hátt og við gerðum í sýnidæmi 1. Útkoman verður eftirfarandi:

   = 4 + 3

Til þess að komast frá upphafspunktinum (2, 2) að endapunktinum (6, 5) þurfum við að fara fjórar rúðulengdir (4) til hægri og þrjár (3) upp. Við sjáum að þetta gefur okkur sjálfkrafa að ofanvarp  á x-ásinn er 4 og samsvarandi vörpun á y-ásinn er 3. Þetta er einfalt að telja út þegar við vinnum með vigra í hnitakerfi. Við getum líka reiknað þetta út með því að finna mismun hnita enda- og upphafspunkts.

   6 − 2 = 4 og 5 − 2 = 3

Eins og kunnugt er þá getum við staðsett vigur hvar sem er í hnitakerfinu. Það er því afskaplega þægilegt að gefa upp vigurinn sem 4 skref til hægri og 3 upp. Einfaldara er að setja þetta fram líkt og hnit enda eru þetta hnit. Þá getum við tjáð vigurinn svona:

    = (4, 3)

Þetta er í raun réttari framsetning en að teikna í hnitakerfi eða gefa upp hnit enda- og upphafspunkts. Það er vegna þess að vigurinn (4, 3) gildir hvar sem er í öllu hnitakerfinu og er ekki háð staðsetningu.

Hnitaframsetning vigra er á þenna veg í mörgum bókum. Gallinn við þessa framsetningu er hins vegar sá að auðvelt er að rugla henni saman við punkthnit og það getur verið þvælið að reikna með hnitunum þegar þau snúa svona. Við munum því í framhaldinu nota eftirfarandi hnitaframsetningu fyrir vigra:

Formúla fyrir hnitum vigurs verður þá eftirfarandi:

Sýnidæmi 4

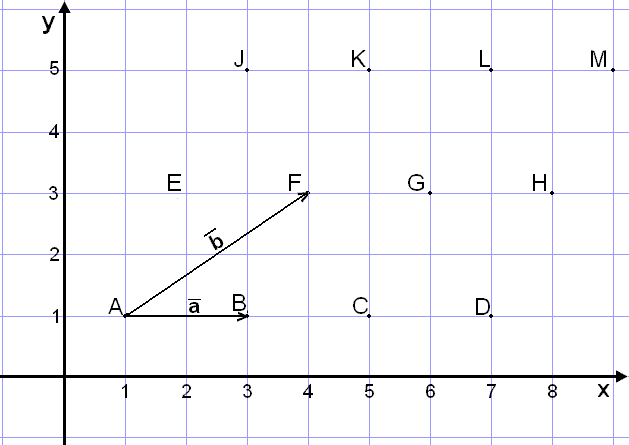
a)   Finnum hnit vigursins =

   Hér förum við tvær rúður til hægri, það er allt og sumt. Ekkert upp eða niður þannig að y-hnitið hlýtur að
    vera 0.

   Við getum líka reiknað þetta eftir formúlunni endapunktur (B) − upphafspunktur (A).

   Við höfum A = (1, 1) og B = (1, 3).

b)   Finnum næst hnit vigursins =

       Við höfum A = (1, 1) og F = (4, 3).

c)   Hvað með hnit vigursins + ? Við sjáum að ef við tengjum og saman þá endum við í punktinum
      G og höfum þá farið 5 rúður til hægri og 2 upp. En við getum einnig reiknað þetta svona:

d)  Skoðum nú hnit vigursins - . Ef við snúum við og tengjum hann við þá lendum við út fyrir
      punktakerfið okkar. Við skulum því byrja á því að snúa við og tengja síðan við hann. Útkoman
     verður vigurinn og hann færir okkur eina rúðu til vinstri og tvær niður. En við getum einnig reiknað
     þetta með hnitum.

e)   Að lokum skulum við finna vigurinn + 2. Ef við tvöföldum vigurinn og tengjum við þá endum við í
      punktinum M. Þá höfum við farið 8 rúður til hægri og fjórar upp. Með hnitum reiknum við þetta svona:

Niðurstaðan af dæmunum hér fyrir ofan er að við getum notað eftirfarandi reglur til þess að leggja saman 
    og finna mismun vigra og margfalda vigra með tölu ef þeir eru á hnitaformi.

Ef gefnir eru vigrarnir og á almennu formi:

og

Þá gilda eftirfarandi reglur:

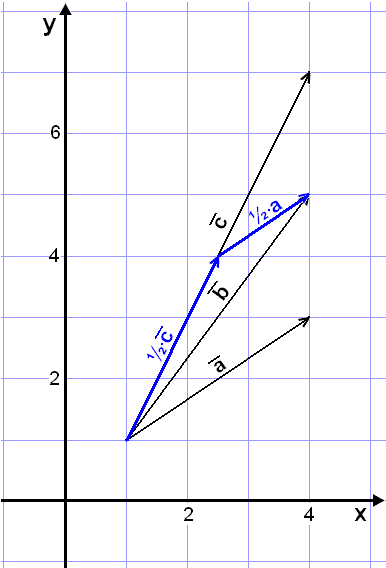
Sýnidæmi 5

Við skulum nú leysa sams konar dæmi og sýnidæmi 3 en að þessu sinni í hnitakerfi og án þess að nota hornafræði.

Gefnir eru vigrarnir , og með eftirfarandi hnit (sjá mynd):

  og

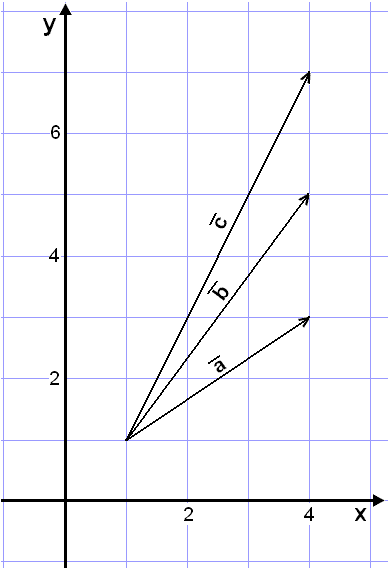
Við skulum nú liða vigurinn samsíða og þannig að eftirfarandi jafna  gildi:   

= r∙ + t∙

Reiknum þetta með hnitum:

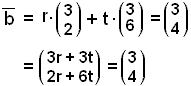
Þetta gefur okkur tvær jöfnur með tveimur óþekktum.

   x-hnitin gefa jöfnuna 3r + 3t = 3 eða r + t = 1 og

   y-hnitin gefa jöfnuna 2r + 6t = 4 eða r + 3t = 2

Við skulum nú leysa saman þetta jöfnuhneppi t.d. með því að draga x-hnitajöfnuna frá y-hnitajöfnunni.

     r + 3t = 2

     −r − t = −1

           2t = 1

             t = ½  og  r = ½

Liðunin verður þá = ½∙ + ½∙  eins og myndin hér fyrir neðan sýnir.

Æfðu þig á þessum aðferðum og taktu síðan próf 2 í Vigrum.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum