Vigrar
| © 2007 Rasmus ehf og Jóhann Ķsak |
Vigrar |
|
Kynning 3
Hnitareikningar meš vigrum
Sżnidęmi 1
Hugsum okkur aš punkturinn A hafi hnitin (2, 2)
og punkturinn B hnitin (6, 5) (sjį mynd). Hnit vigursins
![]() verša:
verša:
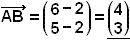
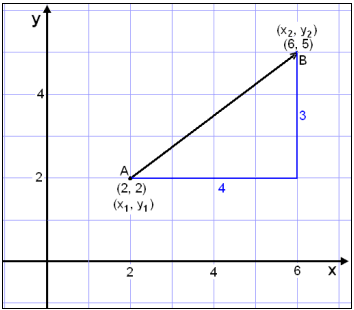
Viš getum nś notaš fjarlęgšarregluna til žess
aš finna vegalengdina į milli A og B og žar meš lengd vigursins
![]() (Sjį Reglu Pżžagórasar, kynningu 2). Reglan er svona:
(Sjį Reglu Pżžagórasar, kynningu 2). Reglan er svona:
![]()
Ef viš setjum inn ķ regluna fįum viš eftirfarandi:
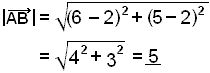
Ķ ljós kemur aš undir kvašratrótinni fįum viš hnit vigursins enda er žetta ekkert annaš en Pżžagórasarregla sett upp fyrir žrķhyrninginn hér fyrir ofan.
Formśla fyrir lengd vigurs er eftirfarandi ef uppafspunkturinn er A = (x1, y1) og endapunkturinn B = (x2, y2).
|
|
Ef viš hins vegar žekkjum hnit vigursins
![]() žį gildir eftirfarandi:
žį gildir eftirfarandi:
|
|
Sżnidęmi 2
Finnum vigurinn
![]() sem er samsķša vigrinum
sem er samsķša vigrinum
![]() en ašeins tveggja eininga langur
(sjį mynd).
en ašeins tveggja eininga langur
(sjį mynd).
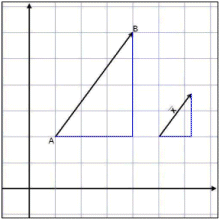
Žrķhyrningarnir į
myndinni eru einslaga žannig aš |![]() |
= t∙|
|
= t∙|![]() |.
Talan t hlżtur aš vera hlutfalliš į milli hliša žrķhyrninganna eša
=
|.
Talan t hlżtur aš vera hlutfalliš į milli hliša žrķhyrninganna eša
= ![]() . Viš getum žvķ
fundiš hnitin į eftirfarandi hįtt:
. Viš getum žvķ
fundiš hnitin į eftirfarandi hįtt:
![]()
Ef vigrarnir
![]() og
og ![]() eru
samsķša žį gildir eftirfarandi regla:
eru
samsķša žį gildir eftirfarandi regla:
|
|
Sżnidęmi 3
Finnum
hvort vigrarnir
![]() og
og
![]() eru samsķša.
eru samsķša.
Ef vigrarnir eru samsķša žį er til tala t žannig
aš jafnan
![]() = t∙
= t∙![]() gildi og sķšan er til önnur tala r žannig aš
jafnan
gildi og sķšan er til önnur tala r žannig aš
jafnan
![]() = r∙
= r∙
gildi einnig. Viš getum nś fundiš t og r śt
frį x-hnitunum og athugaš hvort jafnan gildir žį einnig fyrir y-hnitin.
![]() = t∙
= t∙![]()
![]()
3 = t∙13½ gefur t = 3/13½ =2/9
4 = t∙18 gefur einnig t = 4/18 = 2/9
Vigrarnir
![]() og
og
![]() eru samsķša
eru samsķša
![]() = r∙
= r∙
![]()
3 = r∙6 gefur r = ½
4 = r∙9 gefur hins vegar r = 4/9
Vigrarnir
![]() og
og
eru ekki samsķša (og žį eru
![]() og
og ekki
heldur samsķša)
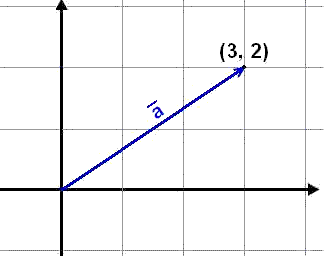
Vigurinn į myndinni hér
fyrir ofan hefur hnitin
![]() .
Uppafspunktinn er (0, 0) og endapunktinn (3, 2) žannig aš vigurinn hefur
greinilega sömu hnit og endapunkturinn og žaš gildir greinilega fyrir alla
vigra sem eiga upphaf ķ mišpunkti hnitakerfisins eša punktinum (0, 0).
.
Uppafspunktinn er (0, 0) og endapunktinn (3, 2) žannig aš vigurinn hefur
greinilega sömu hnit og endapunkturinn og žaš gildir greinilega fyrir alla
vigra sem eiga upphaf ķ mišpunkti hnitakerfisins eša punktinum (0, 0).
| Vigur meš upphafspunkt ķ (0, 0) hefur sömu hnit og endapunkturinn og kallast stašvigur. |
Samkvęmt žessu getum viš tjįš punkt eša staš ķ hnitakerfinu meš stašvigur rétt eins og meš hnitum. Žetta getur veriš įkaflega gagnlegt t.d. žegar viš žurfum aš fęra eitthvaš til ķ hnitakerfinu.
Sżnidęmi 4
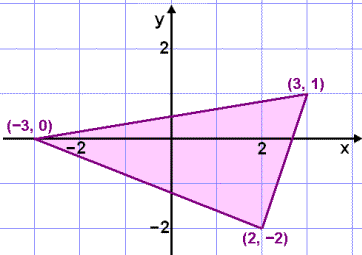
Į myndinni hér fyrir sżnir
žrķhyrning. Viš skulum nś hlišra honum sem nemur vigrinum
![]() .
.
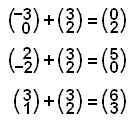
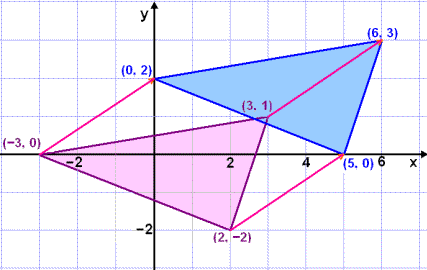
Viš höfum žį fengiš stašvigra nżju hornpunktanna. Myndin hér fyrir nešan sżnir hlišrunina.
Sżnidęmi 5
Viš skulum nś nota stašvigra til žess aš finna mišpunkt lķnustriksins AB ef A = (1, 2) og B = (4, 3).
Viš nefnum mišpunkt hnitakerfisins O (eins og jafnan er gert) og mišpunkt AB köllum viš M. Žį gildir eftirfarandi:
![]() =
=
![]() + ½∙
+ ½∙![]()
Vigurinn
![]() er ķ raun stašvigur
punktsins M og hefur sömu hnit og mišpunkturinn sem viš erum aš leita aš.
Vigurinn
er ķ raun stašvigur
punktsins M og hefur sömu hnit og mišpunkturinn sem viš erum aš leita aš.
Vigurinn ![]() er stašvigur punktsins A og
viš hann žurfum viš aš bęta hįlfum vigrinum
er stašvigur punktsins A og
viš hann žurfum viš aš bęta hįlfum vigrinum
![]() .
Skošum žetta į mynd og reiknum žetta meš
hnitum vigranna.
.
Skošum žetta į mynd og reiknum žetta meš
hnitum vigranna.
Finnum fyrst hnit vigursins
![]() .
.
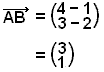
Reiknum sķšan śt
![]() .
.
![]() =
=
![]() + ½∙
+ ½∙![]()
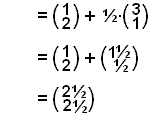
Hnit M eru žau sömu og stašvigursins
![]() eša (2½, 2½).
eša (2½, 2½).
Viš getum aušveldaš okkur reikningana meš žvķ aš bśa til formślu til žess aš finna hnit mišpunkt hvaša lķnustriks AB sem er.
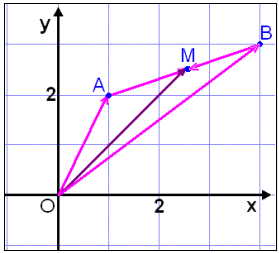
| Viš sjįum aš viš getum nįlgast
mišpunktinn śr bįšum įttum (sjį mynd), frį O um A til M og frį O
um B til M.
Viš getum žvķ sett upp tvęr
vigrajöfnur fyrir
Viš skulum nś leggja žessar tvęr jöfnur saman. |
 |
2![]() =
= ![]() + ½∙
+ ½∙![]() +
+ ![]() - ½∙
- ½∙![]()
![]()
Viš getum sagt aš stašvigur mišpunktsins lķnustriks sé eins konar mešaltal stašvigra endapunkta žess og ef viš reiknum žetta meš hnitum žį finnum viš ķ raun mešaltal x-hnitanna annars vegar og y-hnitanna hins vegar. Žar meš erum viš komin meš mišpunktsregluna sem viš notušum ķ kynningu 2 į reglu Pżžagórasar
| Til žess aš finna mišpunkt
M notum viš eftirfarandi reglu:
Reiknaš meš hnitum veršur reglan svona:
|
Sżnidęmi 6
Žrķhyrningur hefur hornpunktana A = (1, 2), B = (4, 3) og C = (3, 0). Finnum lengd mišlķnu frį horninu A į hlišina BC.
Finnum fyrst mišpunkt BC meš reglunni hér fyrir ofan.
Viš köllum mišpunktinn M
og finnum stašvigur hans
![]() (sjį mynd)
(sjį mynd)
|
|
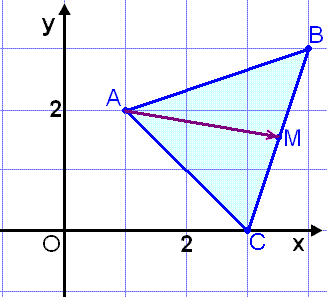 |
Mišpunktur BC hefur sem sagt hnitin M = (3½, 1½).
Finnum nś hnit vigursins
![]() .
.
![]()
Nś getum viš loksins fundiš
lengd vigursins ![]() sem myndar mišlķnuna.
sem myndar mišlķnuna.
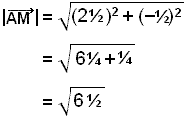
≈ 2,55
| Žaš vęri ekki śr vegi aš finna formślu sem gęfi hnit skuršpunkts mišlķna žrķhyrnings sem er žyngdarpunktur hans (sjį punktinn T į myndinni). Viš getum fundiš formśluna į svipašan hįtt og regluna um mišpunkt lķnustriks. Viš nįlgumst punktinn frį O um öll žrjś hornin og leggjum sķšan saman vigrajöfnurnar. |
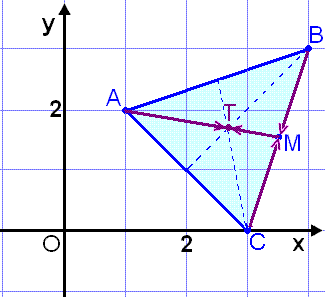 |
Ķ kynningu 2 į žrķhyrningum
var sagt frį žvķ aš mišlķnur ķ žrķhyrningi skerast allar ķ einum
punkti og skipta hvor annarri ķ hlutföllunum 2/1. Samkvęmt žvķ er vigurinn
![]() tvöfaldur į viš
tvöfaldur į viš ![]() žannig aš
žannig aš
![]() =
=
![]() ∙
∙![]() og
og ![]() =
−
=
−![]() ∙
∙![]() .
Viš getum žvķ sett upp eftirfarandi žrjįr jöfnur:
.
Viš getum žvķ sett upp eftirfarandi žrjįr jöfnur:
=
![]() +
+
![]() ∙
∙![]()
=
![]() + ½∙
+ ½∙![]() -
-
![]() ∙
∙![]()
=
![]() - ½∙
- ½∙![]() -
- ![]() ∙
∙![]()
Žegar viš leggjum žessar žrjįr jöfnur saman dettur allt śt nema eftirfarandi:
3
=
![]() +
+ ![]() +
+
![]()
|
|
Žegar viš finnum hnit T reiknum viš mešaltal x-hnitanna sér og y-hnitanna sér. |
Viš getum sem sagt fundiš skuršpunkt mišlķnanna eša žyngdarpunktinn T meš žvķ aš taka eins konar mešaltal af stašvigrum hornpunktanna. Žetta er žvķ greinilega śtvķkkun į mišpunktsreglunni.
Ef viš hins vegar sżndum aš žetta gilti śt frį öllum žremur hornunum žį hefšum viš sannaš aš mišlķnurnar hljóta aš skerast ķ einum punkti og einnig aš reglan um aš mišlķnurnar skipta hvor annarri ķ hlutföllunum 2/1 hlżtur aš gilda.
Sżnidęmi 7
| Finnum skuršpunkt mišlķnanna eša žyngdarpunktinn
T ķ žrķhyrningi sem hefur hornpunktana A = (1, 2), B = (4, 3) og C =
(3, 0) (sjį mynd).
|
|
Žyngdarpunkturinn er T = (2![]() , 1
, 1![]() ).
).
Ęfšu žig į žessum ašferšum og taktu sķšan próf
3 ķ vigrum.
ps. mundu eftir aš fylla śt ķ tékklistann žinn jafnóšum