© 2008  Rasmus ehf    og Jóhann Ísak

Vigrar

Kynning 5

Vigrar og línur

Sýnidæmi 1

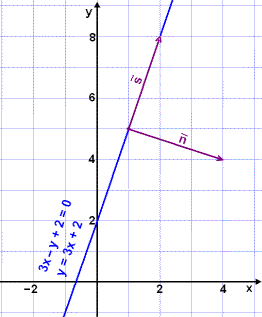
Finnum vigur á línunni y = 3x + 2 og annan vigur sem er hornréttur á hana.

Byrjum á því að finna tvo punkta á línunni.

   Veljum x = 0 og reiknum y. Þá verður y = 3·0 + 2 = 2.

   (0, 2) er á línunni.

   Veljum x = 1 og reiknum y. Þá verður y = 3·1 + 2 = 5.

   (1, 5) er á línunni.

Finnum þá vigurinn á milli punktanna. Við getum kallað hann vegna þess að hann er með sömu stefnu og línan en slíkur vigrur kallast stefnuvigur línunnar. Snúum þessum vigur 90º en þá fáum við vigur sem er hornréttur á línuna og kallast þvervigur og er táknaður með Skoðum þetta á myndinni hér til hliðar.

Við getum umritað jöfnu línunnar y = 3x + 2 í dæminu hér fyrir ofan yfir á formið 3x – y + 2 = 0 með því að færa y yfir jafnaðarmerkið. Þetta form kallast almennt form og við hnjótum um það að stuðlarnir 3 og –1 við x og y eru þeir sömu og hnit þvervigursins . 

Við skulum nú athuga hvort þetta gildir almennt.

Gefum okkur línuna ax + by + c = 0.

Finnum tvo punkta á línunni með því að setja fyrst x = 0 og reikna y og síðan y = 0 og reikna x.

   a·0 + by + c = 0

                    y = –c/b ef x = 0

   ax + b·0 + c = 0

                    x = –c/a ef y = 0

Punktarnir (0, –c/b) og (–c/a, 0) eru á línunni.

Stefnuvigur línunnar verður þá og þvervigurinn .

Það er dálítið óþægilegt að hafa hnitin í brotum þannig að við skulum margfalda þá báða með ab/c. Með þessu erum við að breyta lengd vigranna en þeir verða eigi að síður stefnuvigur og þvervigur línunnar.

     og

Ef við viljum finna stefnuvigur og þvervigur línu þurfum við ekki að gera annað en umrita jöfnu línunnar yfir á almennt form og þá getum við lesið af hnit þvervigurs og stefnuvigurs línunnar.

Í framhaldi af þessu sjáum við fyrir að við getum fundið horn á milli lína með innfeldi stefnuvigra þeirra. Við getum einnig fundið þetta horn með innfeldi þvervigra þeirra sem er sama hornið.

Sýnidæmi 2

Finnum hornið vº á milli línunnar l₁ sem hefur jöfnuna y = 3x + 2 og línunnar l₂ sem hefur jöfnuna y = x + 4 (sjá mynd).

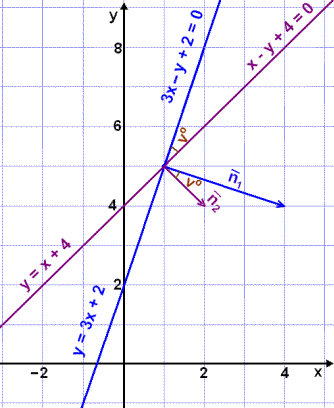
   Almennt form línanna verður 3x – y + 2 = 0 og x – y + 2 = 0.

   Þvervigrar línanna er og

Reiknum lengdir þvervigranna.

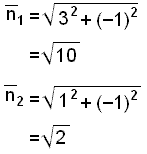
Nú getum við notað innfeldi til þess að reikna hornið á milli þvervigranna sem er hornið vº og sama horn og minna hornið á milli línanna.

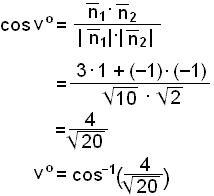
          vº ≈ 26,6º

Hvaða vigrar með upphaf í punktinum (1, 2) skyldu vera

hornréttir á vigurinn

Ef við köllum endapunkt slíks vigurs (x, y) þá getum við sagt að það eru allir vigrar með hnitin

Nú er innfeldi hornréttra vigra 0 þannig að við getum sett upp eftirfarandi jöfnu:

   3(x – 1) + (–1)(y – 2) = 0

              3x – 3 – y + 2 = 0

                    3x – y – 1 = 0

Þetta er almennt form línu sem sker punktinn (1, 2) og hefur þvervigurinn ?

Hér er komin aðferð til þess að finna jöfnu línu út frá einum punkti og þvervigri hennar.

Ef punkturinn (x₁, y₁) er á línu sem hefur þvervigurinn Þá er almenn jafna línunnar eftirfarandi

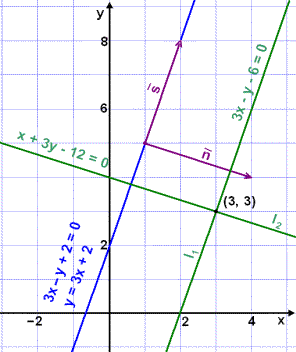
Sýnidæmi 3

Finnum jöfnur tveggja lína l₁ og l₂ sem skerast í punktinum (3, 3). l₁ er samsíða línunni 3x –y + 2 = 0 en l₂ er hornrétt á hana.

  Þvervigur l₁ er sami þvervigur og línan 3x –y + 2 = 0 hefur, eða . Við getum því sett beint inn í jöfnuna.

     a(x – x₁) + b(x – y₁) = 0

   3(x – 3) + (–1)(y – 3) = 0

              3x – 9 – y + 3 = 0

                     3x – y – 6 = 0         (jafna l₁)

  Þvervigur l₂ er stefnuvigur línunnar 3x –y + 2 = 0 eða . Við getum því sett aftur beint inn í jöfnuna.

     a(x – x₁) + b(x – y₁) = 0

       1(x – 3) + 3(y – 3) = 0

              x – 3 + 3y – 9 = 0

                  x + 3y – 12 = 0         (jafna l₂)

Skoðum þetta loks á mynd.

Sýnidæmi 4

Finnum fjarlægðina á milli samsíða línanna 3x – y + 2 = 0 og 3x – y – 6 = 0 (sjá mynd).

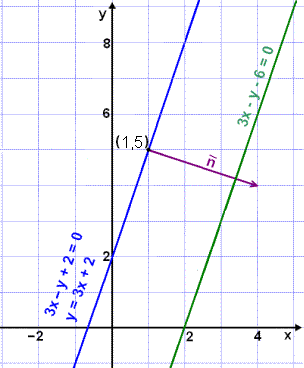
Við skulum velja punktinn (1, 5) á línunni 3x – y + 2 = 0 og finna í hvaða fjarlægð hann er frá línunni 3x – y – 6 = 0. Þá finnum við í leiðinni fjarlægðina á milli línanna.

Við sjáum af myndinni að þvervigurinn er lengri en fjarlægðin á milli línanna. Við skulum því finna tugabrotið t sem við getum margfaldað með þannig að hann verði nákvæmlega jafn langur og bilið er á milli línanna og endapunkturinn (x, y) verði á henni. Við getum þá sett upp eftirfarandi jöfnu:

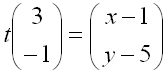
Þetta gefur okkur tvær jöfnur sem við getum leyst m.t.t. x og y.

   3t = x – 1          og          –t = y – 5

     x = 3t + 1                         y = –t + 5

Við skulum nú setja þessar lausnir á x og y inn í jöfnu línunnar.

                       3x – y – 6 = 0

   3(3t + 1) – (–t + 5) – 6 = 0  

         9t + 3 + t  – 5 – 6 = 0 

                               10t = 8

                                   t = 0,8

Í sýnidæmi 2 reiknuðum við lengd vigursins og fengum út .

Fjarlægðin á milli línanna er þá t· eða 0,8·.

Við skulum nú reikna sýnidæmið hér fyrir ofan með bókstöfum einum saman og búa þannig til formúlu til þess að reikna út fjarlægðina á milli punkts og línu.

    Línan hefur almennu jöfnuna ax + by + c = 0 og punkturinn sem við veljum hefur hnitin (x₁, y₁). Við getum 
     þá sett upp eftirfarandi jöfnu:

    Þetta gefur okkur tvær lausnir sem við getum m.t.t x og y.

         ta = x – x₁          og          tb = y – y₁

          x = ta + x₁                        y = tb + y₁

    Setjum þetta inn í jöfnu línunnar og leysum fyrir t.

                              ax + by + c = 0

         a(ta + x₁) + b(tb + y₁) + c = 0

           ta² + ax₁ + tb² + by₁ + c = 0

                                    ta² + tb² = –ax₁ – by₁ – c

                                   t(a² + b²) = –ax₁ – by₁ – c

    Nú er ||² = a² + b² þannig að við getum skrifað þetta svona:

         t·||² = –ax₁ – by₁ – c

    Ef við nú deilum í gegn með ||² fáum við t og síðan margföldum við lengd þvervigurinn  með þessu t. En við verðum að muna að formerki t skiptir ekki máli þannig að við notum tölugildi.

       t = |–ax₁ – by₁ – c| /||²

    Ef við nú margföldum || með þessu fáum við eftirfarandi formúlu:

Sýnidæmi 5

Við skulum nú spegla punktinn (–3, 5) um línuna 3x – y – 6 = 0.

Áætlunin verður á þessa leið. Finnum hornréttan vigur á línuna 3x – y – 6 = 0 sem hefur upphafspunktinn (–3, 5) og endapunktinn P = (x, y) á línunni. Þessi vigur verður þvervigurinn t (sjá mynd). Spegilmyndina S finnum við svo með því að bæta vigrinum t við staðvigur P.

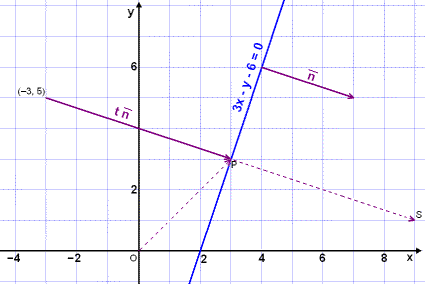
Við þurfum þá að byrja á því að finna töluna t. Við getum sett upp eftirfarandi jöfnur:

Þetta gefur okkur tvær jöfnur sem við getum leyst m.t.t. x og y.

   3t = x + 3        og        –t = y – 5

    x = 3t – 3                    y = –t + 5

Þetta getum við sett inn í jöfnu línunnar og fundið t.

                      3x – y – 6 = 0

   3(3t – 3) – (–t + 5) – 6 = 0

            9t – 9 + t – 5 – 6 = 0

                                 10t = 20

                                     t = 2

Við fáum þá vigurinn og nú getum við feiknað hnit P.

Ef við bætum nú 2  við þennan vigur þá fáum við út staðvigur S.

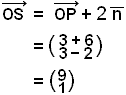
Hnit spegilmyndarinnar er þá S = (9, 1).

Sýnidæmi 6

Við skulum nú finna jöfnur línanna l₁ og l₂ sem skerast í punktinum (3, 4) og eru samsíða vigrunum og .

Síðan skulum við finna jöfnu helmingalínu hornsins á milli þeirra.

Þvervigrar línanna l₁ og l₂ eru og

Jafna l₁ verður þá

   1(x – 3) – 3(y – 4) = 0

        x – 3 – 3y + 12 = 0

             x – 3y + 9 = 0

og Jafna l₂ verður

   3(x – 3) – 1(y – 4) = 0

          3x – 9 – y + 4 = 0 

              3x – y – 5 = 0.

Á helmingalínunni eru allir þeir punktar (x, y) sem eru í sömu fjarlægð frá báðum línunum l₁ og l₂. Við getum því fundið jöfnu hennar með því að setja upp fjarlægðarjöfnuna fyrir fjarlægð (x, y) frá sitt hvorri línunni. Fjarlægðin á að vera jöfn og þá getum við sett jafnaðarmerki á milli.

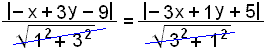
–x + 3y – 9 = ±(–3x + y + 5)

± kemur vegna tölugildisins

Þetta gefur okkur tvær jöfnur.

   –x + 3x + 3y – y – 9 – 5 = 0    eða  –x – 3x + 3y + y – 9 + 5 = 0

                     2x + 2y – 14 = 0                              –4x + 4y – 4 = 0

                           x + y – 7 = 0                                    x – y + 1 = 0

Ástæðan fyrir þessari tvöföldu lausn er að hornin á milli l₁ og l₂ eru í raun tvö, en við skulum skoða þetta á mynd.

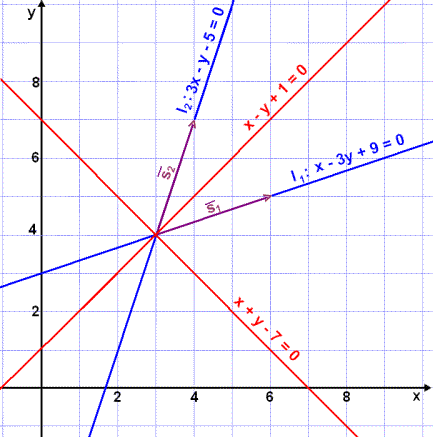
Æfðu þig á þessum aðferðum og taktu síðan próf 5 í Vigrum.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum