© 2007  Rasmus ehf    og Jóhann Ísak

Vigrar

Kynning 6  

Stikaform og pólhnit

Við höfum kynnst því hvernig unnt er að finna tiltekna punkta með því að bæta vigri við hnit punkts eða staðvigurs (sjá kynningu 3). Vigurinn sýndi þá tiltekna stefnu en lengdin var oftar en ekki fundin með því að margfalda hann með tiltekinni tölu t.   

Við getum raunar tjáð beina línu á þennan hátt ef við vitum einn punkt á henni P₁ = (x₁,y₁) og stefnuvigurinn
.

Ef P er breytilegur punktur á línunni þá verður jafna línunnar

= + t·

og með hnitum

Þetta er kallað stikaform línu og algengast er að setja það fram sem jöfnuhneppi þar sem sitt hvor jafnan er fyrir x- og y-hnitin.

Talan t er stikinn sem stikar út línuna með því að taka breytilegt gildi.

Sýnidæmi 1

Við skulum nú finna stikaform línunnar y = 3x + 2.

Almennt form línunnar er 3x – y + 2 = 0 þannig að þvervigur hennar er og stefnuvigur

Ef við veljum síðan x = 1 þá fáum við y = 3·1 + 2 = 5 þannig að punkturinn (1, 5) er á línunni. Stikaform línunnar verður þá t.d. eftirfarandi:

x = 1 + t y = 5 + 3t

Ef við veljum nú t = 1 þá fáum við x = 1 + 1·1 = 2 og y = 5 + 3·1 = 8 sem gefur punktinn (2, 8) sem er á línunni.

Ef við veljum t = 2 þá fáum við x = 1 + 1·2 = 3 og y = 5 + 3·2 = 11 sem gefur punktinn (3, 11).

Ef við nú veljum x = 4 og viljum reikna y þá verðum við að reikna út það t sem samsvarar x = 4 og nota það til þess að reikna y-hnitið.

   x = 1 + t = 4

               t = 4 – 1 = 3

   y = 5 + 3·3 = 14

Sýnidæmi 2

Breytum stikaformi línunnar í sýnidæmi 1 aftur yfir á skurðhallaform.

x = 1 + t      sem gefur t = x – 1 y = 5 + 3t    sem gefur t = (y – 5)/3

Við getum nú sett upp eftirfarandi jöfnu vegna þess að báðar jöfnurnar verða að gefa sama t.

    x – 1 = (y – 5)/3

  3x – 3 = y – 5

  3x + 2 = y

Þetta er sama jafnan og við gengum út frá í sýnidæmi 1.

Sýnidæmi 3

Athugum hvort punkturinn (100, 302) er á línunni

x = 1 + t      y = 5 + 3t

Við reiknum út t samkvæmt báðum jöfnunum.

100 = 1 + t  sem gefur t = 99 302 = 5 + 3t  sem gefur t = (302 – 5)/3 = 297/3 = 99

Við fáum sama t út úr báðum jöfnunum. Punkturinn (100, 302) er á línunni.

Sýnidæmi 4

Finnum skurðpunkt lína sem eru gefnar upp á eftirfarandi stikaformum:

x = 1 + 2t y = 1 + t

og

x = 6 + 3r y = 1 – r

Við  notum sitt hvorn stikann t og r vegna þess að stikar mismunandi lína eru mismunandi breytur sem eiga ekkert sameiginlegt. Hins vegar hljóta x-hnitin að vera hin sömu í skurðpunktinum og sama gildir um y-hnitin. Við getum því sett upp eftirfarandi jöfnuhneppi og leyst það.

   x = 1 + 2t = 6 + 3r

og

   y = 1 + t = 1 – r

Þetta gefur jöfnuhneppið

2t – 3r = 5 t  = –r

Nú getum við sett –r inn í staðin fyrir t í fyrri jöfnunni.

   2(–r) – 3r = 5

             –5r = 5

                 r = –1  og þá er t = 1

Nú getum við reiknað út x og y með því að setja þessar stærðir inn fyrir t eða r í upprunalega stikaforminu.

x = 1 + 2t = 1 + 2·1 = 3 y = 1 + t = 1 + 1 = 2

Prófum líka hina línuna.

x = 6 + 3r = 6 + 3(–1) = 3   y = 1 – r = 1 – (–1) = 2

Skurðpunkturinn er greinilega (3, 2).

Stikaform er sérlega sveigjanlegt og nýtist fyrir mun fleira en framsetningu á beinni línu. Raunar er oft einfalt að tjá samband x og y með stikaframsetningu þó það sé ekki hægt með stökum föllum. Stikaframsetningin er svona sveigjanleg vegna þess að hún byggir á því að sitt hvort fallið með breytuna t stjórnar breytingunum á x og y. Uppsetningin er eftirfarandi:

x = f(t) y = g(t)

Til þess að breyta stikaforminu yfir á jöfnu með breytunum x og y  þá verðum við að leysa báðar stikajöfnurnar m.t.t. t og losa okkur þannig við t-ið.

Sýnidæmi 4

Breytum eftirfarandi stikaformi yfir á venjulegt form með breytunum x og y:

x = t + 1 y = t2 – 1

Út frá efri jöfnunni fáum við t = x – 1 og t² = x² – 2x + 1

Út frá neðri jöfnunni fáum við t² = y + 1. Þetta gefur eftirfarandi:

   y + 1 = x² – 2x + 1

         y = x² – 2x

Þetta er greinilega fleygbogi með núllstöðvar í x = 0 og x = 2.

Við skulum nú teikna hann upp með hjálp stikans. Við látum stikann hlaupa frá –2 til 2 og reiknum x og y.

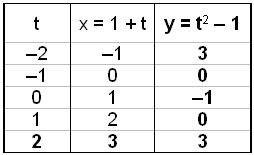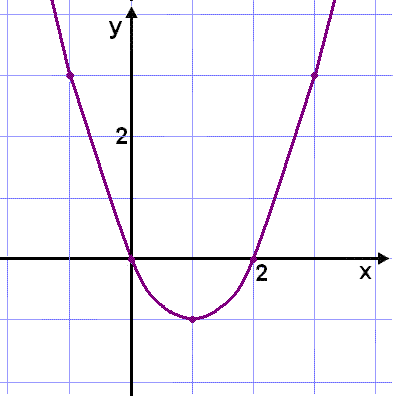Við sjáum að það er fullt eins gott að nota stikan til þess að reikna út gildistöflu eins og að nota eingöngu x og y.

Við getum að sjálfsögðu látið grafísku CASIO-reiknivélina teikna gröf á stikaformi, en til þess þurfum við að stilla gluggann á sérstakan hátt.

Við byrjum á því að velja GRAPH og síðan V-Window með

Þá fáum við upp eftirfarandi valmynd:

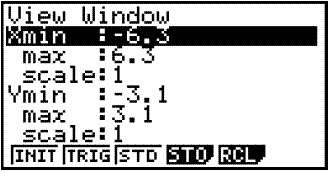
Við getum lofað þessu að vera óhreyfðu með því að velja ör niður fimm sinnum þar til skyggða línan er komin neðst í gluggann. Ef við veljum ör niður einu sinni enn þá opnast nýr gluggi.

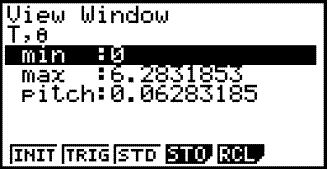Nú þurfum við að stilla t þannig að það hlaupi á sömu gildum og  í gildistöflunni hér á undan þ.a.e. frá -2 til + 2   x (í grafíska glugganum fer út ). q skiptir ekki máli í þessu samhengi. Stillingin verður þá eftirfarandi:

Í þessum glugga þarf að standa Min -2 og max +2 og Pitch t.d. 0,1

Gjarnar útskýra tilgangin með Pitch upp á nákvæmni í útreikningi.

Við þurfum að ýta á í hverri línu til þess að breytingin taki gildi.

Eftir þetta komum við til baka í grafvalmyndina.

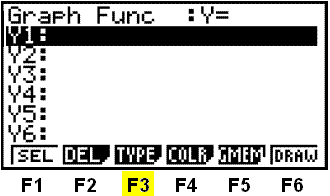
Nú veljum við nýja gerð grafa (TYPE) með F3. Þá birtist lína með nýjum möguleikum neðst á valmyndinni.

Við viljum stikaform (parm.) sem við veljum með F3. Nú kemur aftur upp fyrsta valmyndin en með uppsetningu fyrir stikaform og þá getum við skrifað inn stikaformið (hér litað).

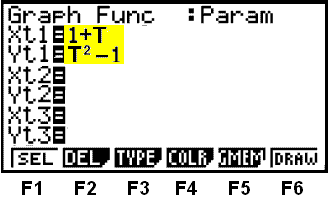
Þegar við skrifum inn T í formúlunni gerum við eins og við höfum venjulega gert með X og notum

Grafið ætti að líta svona út:

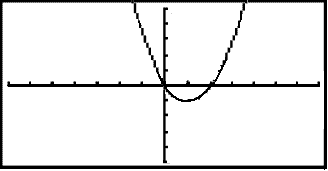
Sýnidæmi 5

Skoðum eftirfarandi stikaform:

x = 4 + 2 cos t y = 3 + 2 sin t

Við skulum leysa út t með því að hefja jöfnurnar í annað veldi og nota okkur regluna cos² t + sin² t = 1 til þess að losa okkur við t.

Efri jafnan gefur okkur x – 4 = 2 cos t  og  (x – 4)² = 4 cos²t.

Neðri jafnan gefur okkur y – 3 = 2 sin t  og  (y – 3)² = 4 sin²t.

Ef við leggjum saman jöfnurnar fáum við eftirfarandi:

   (x – 4)² + (y – 3)² = 4 cos² t + 4 sin² t

                               = 4(cos² t + sin² t)

                               = 4

Niðurstaðan er jafnan (x – 4)² + (y – 3)² = 2² sem er jafna hrings með radíus 2 og miðpunkt í (4, 3).

Hér höfum við kynnst nýrri aðferð, stikaframsetningu, til þess að tjá samhengi breytanna x og y. En það eru einnig til margvísleg hnitakerfi í sléttu, t.d. hnitakerfi þar sem ásarnir eru ekki hornréttir og með mismunandi kvarða.

Við skulum nú skoða kerfi sem er talsvert notað og kallast pólhnitakerfi. Það er tvívítt kerfi sem notast aðeins við einn ás sem kallast pólhnitaás og samsvarar jákvæða hluta x-ássins. Endapunkturinn sem samsvarar 0 á x-ásnum nefnist póll í þessu kerfi. Hver punktur í sléttunni er táknaður með stefnuhorninu sem miðast við pólhnitaásinn og er í fjarlægðinni r frá pólnum (sjá mynd).

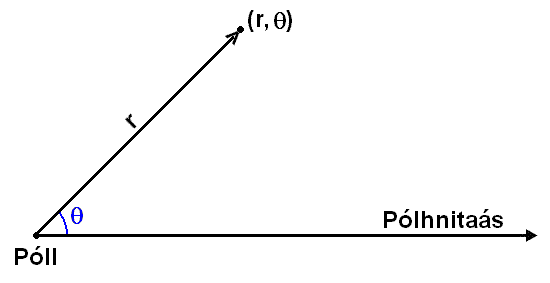
Stærðin (vegalengdin) r er stefnubundin á þann veg að hún getur tekið neikvæð gildi. Ef hornið er á bilinu 0 < < (0º < < 180º) eiga neikvæðu gildin á r við punkta neðan við pólhnitaásinn. Hornið er mælt upp og til vinstri frá pólhnitaásnum eins og venja er. Það getur einnig tekið neikvæð gildi.

Við getum notað pólhnit í rétthyrndu hnitakerfi, en þá hugsum við okkur að pólhnitaásinn falli saman við x-ás hnitakerfisins og póllinn falli saman við miðpunktinn (0, 0).

Sýnidæmi 6

Finnum pólhnit punktsins (3, 4).

Byrjum á því að teikna mynd.

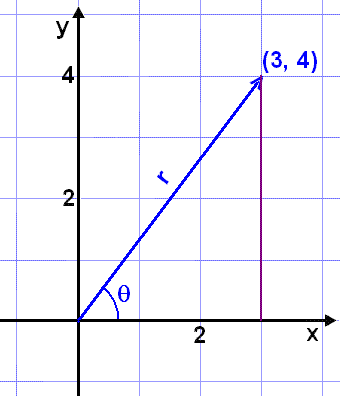
Við sjáum strax að við getum notað reglu Pýþagórasar til þess að finna r.

   r² = 3² + 4² = 9 + 16 = 25

    r = 5

Til þess að finna þurfum við hins vegar að nota hornaregluna tan = mótlæg skh./aðlæg skh. Og finna hornið út frá því.

   q = tan^–1(4/3) ≈ 53,13º ≈ 0,93 rad.

Pólhnit (3, 4) eru því sem næst (5; 0,93).

Þegar við breytum rétthyrndum hnitum yfir í pólhnit þá notum við Pýþagórasarreglu x2 + y2 = r2  til þess að finna r og tan = y/x til þess að finna q.

Sýnidæmi 7

Finnum rétthyrnd hnit punktsins P sem hefur pólhnitin (3, p/4). Byrjum sem fyrr á því að teikna þetta upp í hnitakerfi.

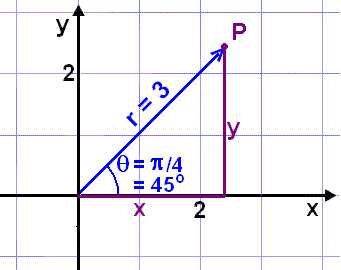
Nú notum við hornareglurnar cos = aðlæg skh./langhl. og sin q = mótlæg skh./langh.

   cos = ^x/₃

          x = 3 cos 45º ≈ 2,12

    sin = ^y/₃

          y = 3 sin 45º ≈ 2,12

Punkturinn P hefur því sem næst hnitin (2,12; 2,12)

Unnt er að teikna gröf pólhnita þar sem r og eru háð ákveðnum skilyrðum. T. d. ef er fasti og r getur tekið öll gildi þá kemur fram bein lína í gegnum pólpunktinn. Ef hins vegar ef r er fasti og getur tekið öll gildi á bilinu 0 < < 2 þá er grafið hringur með miðju í pólpunktinum og radíus sem samsvarar fastanum.

Pólhnitajöfnur eru oftast settar fram á forminu r = f(q).

Ef við viljum breyta pólhnitajöfnum yfir í venjuleg rétthyrnd hnit þá verðum við að beita reglunum hér fyrir neðan ásamt talsvert flókinni algebru. Við skulum nú skoða nokkur dæmi um það.

Sýnidæmi 8

Finnum jöfnu fyrir rétthyrnd hnit ef pólhnitajafnan er eftirfarandi:

    r = 4/(cos – sin )

Við skulum byrja á því að margfalda í gegn með (cos + sin ) og nota síðan reglurnar x = r cos   og  y = r sin .

   r (cos – sin ) = 4

   r cos – r sin = 4

                    x – y = 4

                          y = x – 4

Pólhnitajafnan r = 4/(cos – sin ) jafngildir jöfnunni y = x – 4.

Sýnidæmi 9

Finnum jöfnu fyrir rétthyrnd hnit ef pólhnitajafnan er eftirfarandi:

    r = 2(cos + sin + 1/r)

Nú margföldum við í gegn með r til þess að geta notað reglurnar.

           r² = 2(r cos + r sin + 1)

   x² + y² = 2(x + y + 1)

   x² + y² = 2x + 2y + 2

Þetta er farið að líta kunnuglega út.

      x² – 2x + y² – 2y = 2

Við skulum nú bæta 2 við sitt hvoru megin við jafnaðarmerkið.

   x² – 2x + 1 + y² – 2y + 1 = 2 + 2

   (x – 1)² + (y – 1)² = 2²

Þetta er jafna hrings með miðju í (1, 1) og radíus 2.

Sýnidæmi 10

Skoðum graf pólhnitajöfnunnar r = 5 sin 3.

Við getum reynt að koma þessu yfir á rétthyrnd hnit en það lítur ekki vel út.

Byrjum á því að umrita sin 3.

   sin 3 = sin (2 + )

Nú getum við beitt samlagningarreglunni og síðan reglunni um sínus af tvöföldu horni. Einnig er hægt að fletta þessu upp í formúlusöfnum.

   sin 3 = 3 sin + 4 sin³

Með þessu getum við umritað dæmið.

   r = 15 sin + 20 sin³

Við skulum nú margfalda í gegn með r³ til þess að nýta okkur að y = r sin .

   r⁴ = 15 r²·r sin + 20 r³ sin³

       = 15 r² y + 20 y³

Nú getum við beitt reglunni r² = x² + y² sett x² + y² inn fyrir r².

                      r⁴ = 15 r² y + 20 y³

           (x² + y²)² = 15 (x² + y²)y + 20 y³

   x⁴ + 2x²y² + y⁴ = 15x²y + 15y³ + 20 y³

Við höfum nú umritað jöfnuna yfir í rétthyrndt hnitaform og niðurstaðan er miklu flóknari en pólhnitajafnan sem við lögðum upp með. Við verðum því að nota pólhnitaformið til þess að teikna grafið. Setjum upp gildistöflu.

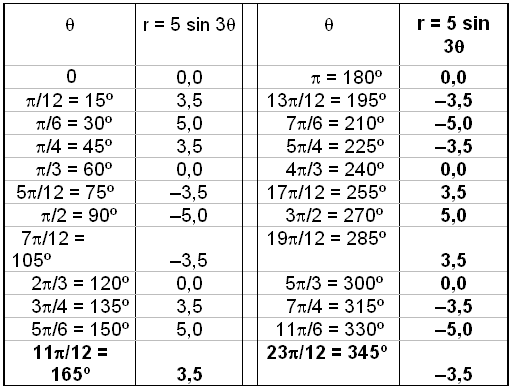
Við skulum nú búa til hnitakerfi sem lítur út eins og kóngulóarvefur. Þá getum við auðveldlega sett inn punktana úr gildistöflunni og rissað grafið. Við setjum inn einn punkt fyrir hvert horn og r segir til um hve langt frá pólnum hann á að vera.

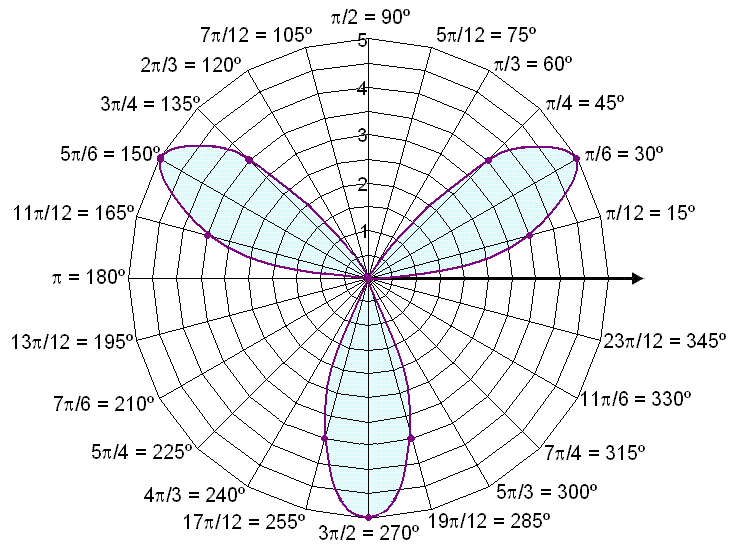
Grafið myndar eins konar þriggja blaða smára eins og sjá má á myndinni.

En við getum einnig látið grafísku reiknivélina hjálpa okkur.

Þá byrjum við á því að stilla vélina á radíana með SHIFT og SET UP. Síðan þurfum við að stilla af gluggann en það gerum við með því að velja GRAPH og síðan V-Window með .

Þá fáum við upp gamalkunna valmynd:

Við getum lofað þessu að vera óhreyfðu og veljum  ör niður sex sinnum til þess að komast í gluggann fyrir neðan. þá opnast nýr gluggi.

Hér setjum við inn gildi eins og myndin sýnir. Lágmarkið (min) er 0 en hámarkið (max) er 6,283185 3 sem er því sem næst 2. Með þessu látum við hornið stika heilan hring og skrefstærðin (pitch) er 2/100. 

Við þurfum að ýta á í hverri línu til þess að breytingin taki gildi.

Eftir þetta komum við til baka í grafvalmyndina.

Nú veljum við nýja gerð grafa (TYPE) með F3. Þá birtist lína með nýjum möguleikum neðst á valmyndinni.

Við veljum möguleikann r = með F2. Nú kemur aftur upp fyrsta valmyndin en með uppsetningu fyrir pólhnit og þá getum við skrifað inn pólhnitajöfnuna eins og sýnt er (sjá gulu línuna) hér fyrir neðan.

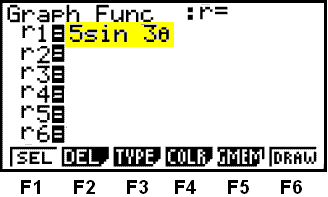
Þegar við skrifum inn q í formúlunni gerum við eins og við höfum

 áður gert með breytuna x og notum

Grafið ætti að líta svona út:

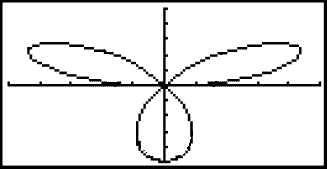
Æfðu þig á þessum aðferðum og taktu síðan próf 6 í vigrum.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum