© 2007  Rasmus ehf    og Jóhann Ísak

Keilusnið

Kynning 1  

Brennipunktur og leiðilína fleygboga

Hugsum okkur tvær keilur þannig að önnur er á haus upp af hinni (sjá mynd). Í stæðfræðilegum skilningi gerum við ráð fyrir að keilurnar taki engan enda upp á við eða niður á við. Það má líta svo á að svona keilur verði til þegar lóðrétt lína l og skáhöll lína m skerast og skáhöllu línunni er snúið 360º um hina.

Hugsum okkur nú að við skerum keilurnar með spjöldum eins og sýnt er á myndinni. Stærðfræðilega séð hugsum við okkur að þessi spjöld tákni sléttur sem teygja sig óendanlega langt í allar áttir og eru báðar með sitt hvort tvívíða, hornrétta hnitakerfið. Þegar þessar sléttur skera keiluyfirborðið koma fram ferlar sem nefndir hafa verið keilusnið. Mikið hefur verið fjallað um þessa ferla í meira en 2000 ár, enda eru m.a. brautir himintungla keilusnið. Keilusnið koma einnig mikið við sögu í nútímanum því lögun holspegla í sjónaukum og ljóskösturum eru keilusnið og sama máli gegnir um gerfihnattaloftnet o.m.f.

Keilusnið hafa formúluna Ax² + Bxy + Cy² + Dx + Ey + F = 0 þar sem x og y eru breytur eins og vant er og A, B, C, D, E og F eru rauntölur.

Við höfum nú þegar fjallað talsvert um tvo ferla af þessari gerð, hringinn og fleygbogann. Hringurinn kemur fram ef skurðsléttan er lárétt (sjá efra spjaldið á myndinni). Hann kemur fram ef stuðullinn við xy er 0 og stuðlarnir við x² og y² þurfa að vera jafnir, þannig að jafna hrings er eftirfarandi:

    Ax² + Ay² + Bx + Cy + D = 0

Í umfjölluninni um hringinn þáttuðum við hann yfir á eftirfarandi form:

   (x – h)² + (y – k)² = r²  

   þar sem (h, k) er miðpunktur hringsins og r er radíus hans.

Fleygbogi kemur fram ef skurðsléttan er samsíða hlið keilunnar (sjá neðra spjaldið á myndinni). Þá eru stuðlarnir við xy og y² báðir 0 og formúlan verður kunnugleg.

   y = Ax² + Bx + C

Sýnidæmi 1

Skoðum hvaða punktar eru í sömu fjarlægð frá punktinum F = (0, 1) og láréttu línunni y = – 1. Ef P = (x, y) er punktur á þessum ferli þá er vigrarnir og jafn langir (sjá mynd).

Nú skulum við reikna lengdir þessara vigra í öðru veldi (til þess að losna við kvaðratrót.

||² = (y + 1)² = y² + 2y + 1

||² = (x – 0)² + (y – 1)² = x² + y² – 2y + 1

Þetta á að vera jafnt þannig að við getum sett upp eftirfarandi jöfnu og einfaldað:

                  4y = x²

                    y = ¼ x²

Við höfum sem sagt fengið út að þeir punktar sem eru í sömu fjarlægð frá F = (0, 1) og láréttu línunni y = – 1 mynda fleygboga sem er keilusnið.

Nú getum við skilgreint fleygboga á eftirfarandi hátt:

Fleygboginn y = ¼ x² hefur samkvæmt þessu leiðilínuna y = –1 og brennipunktinn F (0, 1).

Botnpunktur þessa fleygboga er (0, 0) eins og kemur fram í sýnidæminu hér fyrir ofan. Við skulum nú hliðra fleygboganum þannig að botnpunkturinn verði (2, 3). Jafnan verður þá

   y = ¼(x –2)² + 3

brennipunkturinn verður

   F = (0+2, 1+3) = (2, 4)

og leiðilínan

   y = –1 + 3 = 2

Við skulum nú reikna sambærilegt dæmi og hér fyrir ofan með bókstöfum og búa þannig til almennar reglur.

Ef við segjum F vera punktinn (0, q) og leiðilínuna y = –q þá fáum við út eftirfarandi fleygboga:

Ef við hliðrum nú þessum fleygboga þannig að hann fái botnpunktinn (h, k) þá verður jafnan

Þar sem |q| er nú bilið á milli brennipunktsins og botnpunktsins. Nú verðum við raunar hætta að tala um botnpunkt fleygbogans vegna þess að við vitum ekki lengur hvernig hann snýr. Ef q er neikvæð stærð er það vegna þess að brennipunkturinn er fyrir neðan „botnpunktinn“ þannig að hann er ekki lengur botnpunktur heldur topppunktur. Í erlendum tungumálum hefur þessi topp- eða botnpunktur verið nefndur einu nafni „vertex“ sem við höfum ekki betri þýðingu á en topppunktur og við skulum því nota það hugtak hvernig svo sem fleygboginn kann að snúa.

Brennipunktur fleygbogans verður nú

   F = (h, k+q)

og leiðilínan

   y = k – q

þar sem q er bilið á milli brennipunkts og topppunkts fleygbogans.

Ef við nú fáum fleygbogann á forminu

   y = a(x – h)² + k

þá er a = 1/4q og q = 1/4a. Brennipunkturinn verður þá

   F = (h, 1/4a + k)

og leiðilínan

   y = k – 1/4a

Skoðum nú það form fleygboga sem við erum einna vönust.

   y = ax² + bx + c

Byrjum á því að margfalda upp úr jöfnunni hér fyrir ofan.

   y = a(x – h)² + k

      = a(x² – 2hx + h²) + k

      = ax² – 2ahx + ah² + k

Berum þetta saman við almennu jöfnuna.

   y = ax² + bx + c

Við fáum b = –2ah og þá er h = –b/2a sem er kunnugleg jafna fyrir samhverfuás fleygboga og c = ah² + k sem gefur k = c – ah² = c – a(–b/2a)² = c – b²/4a. Nú fáum við topppunktinn

   T = (h, k) = (–b/2a, c – b²/4a)

og brennipunktinn

   F = (h, 1/4a + k) = (–b/2a, 1/4a + c – b²/4a)

Ef við gerum brotin samnefnd og setjum upp á strik fáum við eftirfarandi:

Leiðilínan verður samkvæmt þessu y = k – 1/4a = c – b²/4a – 1/4a sem við getum sett upp á eitt strik.

Þessar formúlur eru nokkuð flóknar þannig að mörgum finnst einfaldara að reikna fyrst út topppunktinn og finna síðan brennipunktinn og leiðilínuna út frá honum. Við skulum hafa eftirfarandi í huga:

Samantekt

Formúla	y = a(x – h)2 + k	y = ax2 + bx + c
Topppunktur	T = (h, k)	T = (–b/2a, c – b2/4a)
Brennipunktur	F = (h, 1/4a + k)
Leiðilína	y = k – 1/4a

Sýnidæmi 2

Finnum topppunkt fleygbogans y = x² – 2x + 3 og síðan brennipunkt hans og leiðilínu.

Hér höfum við a = 1, b = –2 og c = 3 og gætum sett það inn í formúlurnar hér fyrir ofan en einfaldast er að gera þetta svona:

Út frá þessari umritun getum við lesið að topppunkturinn er (1, 2) þannig að h = 1 og k = 2. Reiknum þá brennipunktinn næst.

   F = (h, 1/4a + k)

      = (1, ¼ + 2)

      = (1, 2¼)

Leiðilínan er þá

    y = k – 1/4a

       = 2 – ¼

    y = 1¾

Sýnidæmi 3

Skoðum nú fleygboga með brennipunkt í punktinum (4, 0) á x-ásnum og lóðrétta leiðilínu í x = – 4 (sjá mynd).   

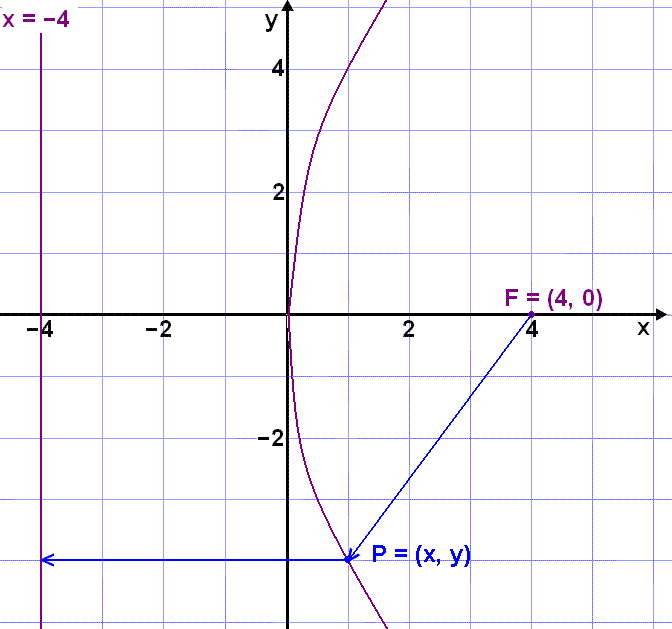
Nú verður jafnan eftirfarandi:

           (x + 4)² = (x – 4)² + (y – 0)²

    x² + 8x + 16 = x² – 8x + 16 + y²

                 16x = y²

Við sjáum að þetta er ekki hægt að umrita sem fall á forminu y = f(x) en eigi að síður er þetta fleygbogi.

Sýnidæmi 4

Notum grafíska CASIO reiknivél til þess að finna topppunkt og brennipunkt fleygbogans x = (y – 2)² + 3 og teikna hann upp.

Við byrjum á því að velja CONICS í aðalvalmyndinni.

Síðan þurfum við að stilla gluggann og förum í V-Window með .

Við getum t.d. valið eftirfarandi stillingar:

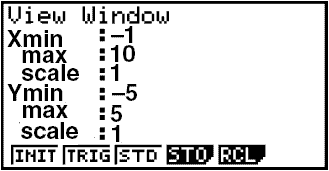
Nú getum við valið ýmis keilusnið en við veljum efsta möguleikann með því að ýta á .

Eftir þetta fáum við upp eftirfarandi valmynd:

Ef við veljum DRAW með F6 þá fáum við upp grafið. Þetta virðist í fljótu bragði vera endastöð og skjámyndin gefur ekki upp neina valmöguleika. Ef við hinsvegar veljum F5 (G-Solv) og síðan F1 (þar stendur FOCS fyrir focus) fáum við eftirfarandi skjámynd:

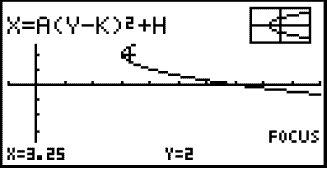
Þetta segir okkur að brennipunkturinn er (3¼, 2).

Ef við nú förum til baka með , veljum F5 (G-Solv) og

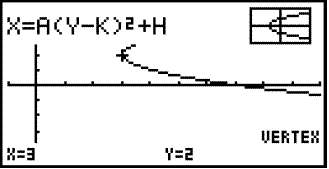
Þetta gefur okkur topppunkt fleygbogans sem er (3, 2).

Við getum haldið áfram á sama hátt og valið F5 (G-Solv) og síðan F2 (þar stendur SYM fyrir symmetry) og þá fáum við upp að samhverfuás fleygbogans er y = 2.

Þessu næst getum við valið F5 (G-Solv) og síðan F3 (þar stendur DIR fyrir directrix) og þá fáum við upp að leiðilínan er x = 2¾.

Að lokum getum við valið F5 (G-Solv) og síðan aftur F5 (þar stendur LEN fyrir length) en þá fáum við upp L = 1 sem er  breidd fleygbogans ef mælt er þvert á samhverfuásinn í gegnum brennipunktinn.

Sýnidæmi 5

Setjum nú upp pólhnitajöfnu fyrir fleygboga með brennipunkt í (0, 0) og leiðilínu í x = 4.

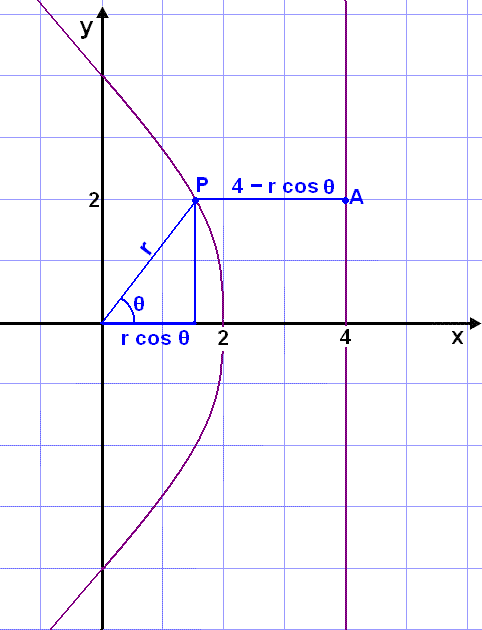
Við sjáum á grafinu að hér gildir að r = PA = 4 – r cos q.

Pólhnitajafnan verður því eftirfarandi ef við leysum hana m.t.t r:

                    r = 4 – r cos q

     r + r cos q = 4

   r(1 + cos q) = 4

                    r = 4/(1 + cos q)

Við skulum nú breyta þessu í jöfnu með rétthyrndum hnitum.

Að lokum getum við teiknað upp báðar gerðirnar í reiknivélinni til þess að sjá hvort við fáum sama fleygbogann.

Sýnidæmi 6

Finnum jöfnu fleygboga sem hefur brennipunktinn F = (4, 5) og topppunktinn T = (2, 5).

Við sjáum að bæði T og F liggja á línunni y = 5. Fjarlægðin á milli þeirra miðað við x-ás er 2 og T er mitt á milli F og leiðilínunnar þannig að leiðilínan er y-ásinn.

Við getum sett upp jöfnun þessa fleygboga á forminu x = a(y – k)² + h og við vitum nú þegar að h = 2 og k = 5 (T = (h, k) = (2, 5)). Okkur vantar því aðeins stuðulinn a.

Nú getum við séð út frá formúlunum hér fyrir ofan að bilið á milli brennipunkts og topppunkts er 1/4a. Við getum því sett upp eftirfarandi jöfnu og leyst út a.

        2 = 1/4a

   4a·2 = 1

        a = ⅛

Jafna fleygbogans er því x = ⅛ (y – 5)² + 2

Æfðu þig á þessum aðferðum og taktu síðan próf 1 í keilusniðum.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum