© 2008 Rasmus ehf og Jóhann Ķsak
|
© 2008 Rasmus ehf og Jóhann Ķsak |
Markgildi |
|
Markgildi og bilskipt föll
Hvert stefna föll ef x stefnir į óendanlegt? Hękka žau upp śr öllu valdi eša lękka žau aftur eša nį žau einhverju tilteknu gildi? Viš vitum aš ekki er unnt aš deila meš nślli, en hvaš gerist ef viš deilum meš tölu sem er nęstum nśll? Hoppar grafiš upp eša nišur eša veršur ašeins eftir örsmįtt gat ķ grafinu. Markgildi og stęršfręšin sem žeim tengist fęst viš spurningar af žessum toga.
Skošum falliš
![]()
Grafķsk CASIO-reiknivél teiknar upp beina lķnu (sjį mynd) įn žess aš žaš trufli hana nokkuš aš ķ x = 1 er deilt meš nślli og falliš er ekki skilgreint žar (Ff = R\{1}).
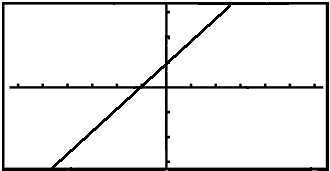
En skošum nś hvaš gerist žegar x nįlgast 1. Ķ stęršfręšinni er hefš fyrir žvķ aš tįkna žetta į eftirfarandi hįtt:
![]()
Lim er skammstöfun fyrir limes sem kemur śr latķnu og žżšir markgildi. Rithįtturinn hér fyrir ofan merkir žvķ markgildiš sem falliš stefnir į žegar x stefnir į 1.
Viš getum notaš venjulega algebru į brotiš og einfaldaš žaš, en viš megum ekki missa sjónar į upphaflega brotinu og vandamįlinu sem kom upp vegna deilingar meš nślli.
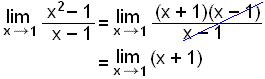
Nś er deiling meš nślli ekki til stašar lengur žannig aš viš getum reiknaš žetta beint og sett 1 inn fyrir x (reiknaš f(1)).
![]() = 1 + 1 = 2
= 1 + 1 = 2
Žetta segir okkur aš falliš ![]() stefnir į tvo žegar x nįlgast 1.
stefnir į tvo žegar x nįlgast 1.
|
|
Graf f(x) hefur ķ raun eyšu eša gat ķ x = 1 (sjį grafiš hér til vinstri). Viš getum hins vegar skilgreint fall sem byggir į sömu stęšu en hefur samfellt (eša samhangandi) graf en žaš er falliš g(x) eins og žaš er sett upp hér fyrir nešan. |
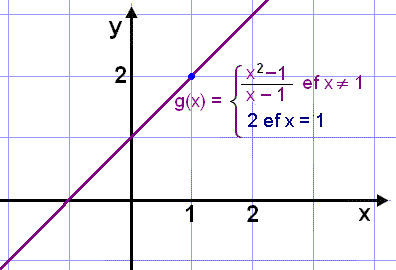 |
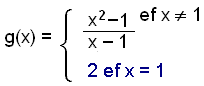
Meš žessu veršur grafiš samfelld lķna eins og grafiš hér til hęgri sżnir. |
Bilskipt föll nefnast svona föll sem eru skilgreind meš fleiri en einni formślu hįš žvķ hvaša gildi x tekur eins og falliš g(x) hér fyrir ofan eša hįš tilteknu bili mišaš viš x-įsinn.
Finnum markgildiš ![]()
Hér er engin deiling meš nślli eša nokkurt annaš sem bannar okkur aš reikna žetta beint. Viš getum žvķ sett 2 ķ staš x ķ formślunni.
23 22 = 8 4 = 4
Falliš f(x) = x3 x2 stefnir į 4 žegar x nįlgast 2 (śr bįšum įttum ef svo ber undir).
Finnum markgildiš
![]()
Hér getum viš ekki sett žrjį inn fyrir x žvķ žį fįum viš deilingu meš nślli. Hins vegar getum viš žįttaš fyrir ofan strik og sķšan stytt brotiš.
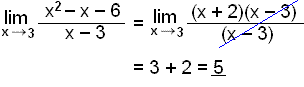 |
Hér setjum viš 3 inn fyrir x. |
Finnum markgildiš ![]()
Nś getum viš ekki stytt neitt. Eina śrręšiš er aš skoša markgildiš meš žvķ aš setja inn tölur sem nįlgast 1 śr bįšum įttum (bęši ofan frį og nešan frį), en byrjum į žvķ aš reikna śt gildistöflu og teikna graf
![]()
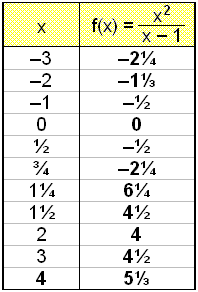 |
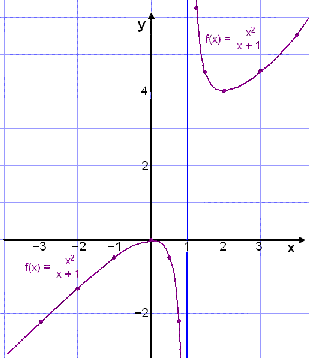 |
Grafiš er ķ tvennu lagi og leggst aš lóšréttri ašfellu ķ x = 1.
Viš skulum nś skoša hvaš gerist žegar viš nįlgumst x = 1, en grafiš sżnir aš viš veršum aš gera žaš śr sitt hvorri įttinni. Fljótlegast er aš gera žetta ķ töflureikninum EXCEL. Viš skrifum tölur sem koma nęr og nęr 1 ķ A- og D-dįlkana. Formślan ķ reitnum B3 veršur =A3^2/(A31) žar sem A3 reiturinn geymir breytuna x. Samsvarandi formśla kemur ķ reitinn E3 eša = D3^2/(D11). Formślurnar eru afritašar nišur.
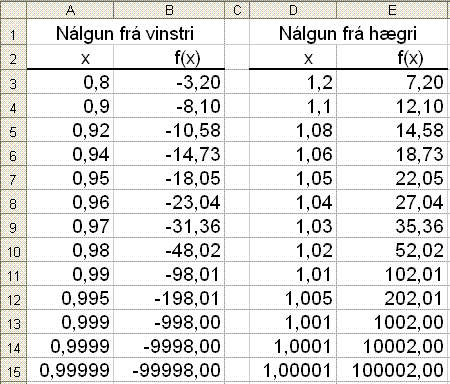
Viš sjįum aš žegar viš nįlgumst 1 frį vinstri (frį neikvęša hluta x-įssins) lękka tölurnar ķ f(x) dįlknum (B-dįlknum) stöšugt og stefna į ∞. En žegar viš nįlgumst 1 frį hęgri stefnir f(x) hins vegar į +∞. Nś er óendanlegt ekki nein tiltekin tala. Ef viš veljum einhverja ógnarstóra tölu žį er ęvinlega hęgt aš benda į einhverja enn stęrri. Nišurstašan er žvķ eftirfarandi:
Markgildiš ![]() er ekki til.
er ekki til.
Skošum markgildiš ![]() .
.
Viš sjįum aš žetta markgildi er ekki hęgt aš nįlgast frį vinstri vegna žess aš ekki er hęgt aš draga kvašratrót af neikvęšum tölum. Žegar svona stendur į er rétt aš taka žaš fram aš markgildiš eigi aš vera frį hęgri. Žaš er gert meš eftirfarandi rithętti:
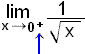
Plśsinn
merkir frį hęgri.
Grafķsk CASIO-reiknivél sżnir grafiš svona:
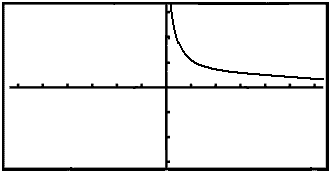
Grafiš kemur nišur meš y-įsnum og leggst sķšan aš x-įsnum. Žaš veršur aldrei neikvętt og er ekki til fyrir neikvęšar tölur. Ef viš setjum inn tölur mjög nįlęgt nślli žį fįum viš mjög stórar tölur śt. Žaš er žvķ ljóst aš grafiš stefnir į óendanlegt žegar x stefnir į nśll frį hęgri. Markgildiš er ekki til.
Finnum markgildiš ![]()
Žaš liggur ekki ķ augum uppi hvernig hęgt er aš einfalda žetta brot en ef viš höfum ķ huga samokaregluna (a b)(a + b) = a2 b2 rennur žetta upp.
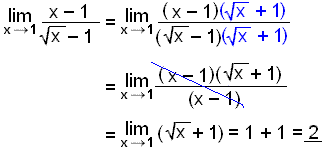
|
Lausn markgildis f(x) žar sem x stefnir į tiltekna tölu a er f(a) (talan a er sett inn fyrir x).
Hins vegar ef f(x) hefur breytuna x ķ nefnara brots žį getur komiš upp deilng meš nślli. Žį er eina rįšiš aš einfalda brotiš meš žįttun og styttingu. |
|
|
Gefum okkur eftirfarandi
bilskipt fall: |
Ķ žessu tilviki getum viš ekki fundiš eitt einstakt markgildi fyrir f(x) žegar x stefnir į 1 og sagt er aš falliš sé ekki samfellt ķ x = 1. Hins vegar getum viš fundiš markgildi frį vinstri og hęgri.
![]() og
og ![]()
|
Falliš f(x) er samfellt ķ punktinum (a, f(a)) ef žaš er skilgreint (er til) ķ grennd viš x = a og
Ef žetta gildir fyrir sérhvern punkt ķ formengi f(x) žį getum viš stašhęft aš falliš hljóti aš vera samfellt ķ öllu formenginu. Sama gildir um eitthvert opiš bil sem viš veljum. Viš getum slegiš žvķ föstu aš falliš hljóti aš vera samfellt į bilinu ef žaš er samfellt ķ sérhverjum punkti į bilinu. |
Viš skulum nś skoša markgildi žar sem x stefnir į + eša óendanlegt.
Žetta er sjaldan neitt flókiš ef falliš er margliša. Žegar įkvešnu stigi er nįš halda slķk föll įfram aš vaxa eša minnka žegar veljum hęrri eša lęgri x. Sama gildir um logra, vķsisföll og kvašratrótarföll.
Um ręš föll (brot į forminu f(x)/g(x)) gildir hins vegar öšru mįli.
Ef viš žurfum aš leysa
markgildi af geršinni ![]() veršum viš aš skoša sérstaklega hvort fallanna teljarinn f(x) eša
nefnarinn g(x) vex (eša minnkar) hrašar.
veršum viš aš skoša sérstaklega hvort fallanna teljarinn f(x) eša
nefnarinn g(x) vex (eša minnkar) hrašar.
Ef f(x) vex hrašar žį er markgildiš ekki til vegna žess aš brotiš stefnir į + eša óendanlegt žegar x stefnir į óendanlegt.
Hins vegar ef g(x) vex hrašar žį er markgildiš vęntanlega einhver įkvešin tala.
Skošum nokkur markgildi žar sem x stefnir į óendanlegt.
a)
![]()
Hér stefnir nefnari brots į óendanlegt į mešan teljarinn
breytist ekki. Brotiš fer žvķ stöšugt minnkandi og
markgildiš stefnir į nśll.
![]()
b)
![]()
Hér vex nefnari brotsins
hrašar en teljarinn og markgildiš stefnir žvķ į nśll.
![]()
c)
![]()
Hér vex teljarinn hrašar
en nefnarinn. Markgildiš stefnir žvķ į óendanlegt og er ekki til.
d)
![]()
Hér er hęrra veldi ķ
nefnaranum žannig aš hann vex hrašar en teljarinn og markgildiš stefnir į nśll.
![]()
|
hefur
lausnina 0 ef |
Finnum markgildiš ![]() .
.
Hér eru veldin jöfn fyrir ofan og nešan strik. Hér er žvķ ekki um žaš aš ręša aš nefnari vaxi hrašar en teljarinn (eša öfugt). Ef viš deilum hins vegar ķ alla liši brotsins meš x ķ hęsta veldinu (sem er x2) veršur dęmiš leysanlegt.
![]()
Viš vitum aš brot žar sem hęrra veldi er ķ nefnaranum stefna į nśll žegar x stefnir į óendanlegt. Ķ raun veršur ekkert eftir annaš en stušlarnir viš hęsta (annaš) veldiš. Nišurstašan veršur žvķ eftirfarandi:
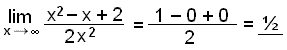
|
Markgildi žar sem marglišur af sama stigi (jafn hį veldi) eru fyrir ofan og nešan strik mį leysa meš žvķ aš deila ķ gegn meš breytunni ķ hęsta veldinu (stiginu) sem kemur fyrir ķ stęšunni. |
Ęfšu žig į žessum ašferšum og taktu sķšan próf
1 ķ markgildum.
ps. mundu eftir aš fylla śt ķ tékklistann žinn jafnóšum