© 2008 Rasmus ehf og Jóhann Ķsak
|
© 2008 Rasmus ehf og Jóhann Ķsak |
Afleišur |
|
Vaxtarhraši og halli snišla og snertla
Kynnum nś til sögunnar tvenns konar lķnur.
Lķna sem sker a.m.k. 2 punkta į grafi nefnist snišill.
Lķna sem snertir graf ķ einum punkti žannig aš grafiš og lķnan hafi sama halla ķ punktinum nefnist snertill.
Skošum žetta į mynd.
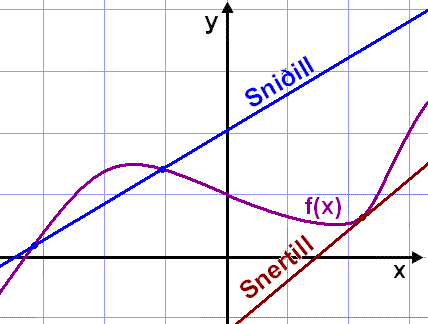
Hugum fyrst aš hugtaki sem kallast vaxtarhraši og mešalvaxtarhraši. Vaxtarhraši er męlikvarši į žaš hve hratt eitthvaš vex. Mešalvaxtarhraši er hins vegar eins og nafniš bendir til eins konar mešaltalsvöxtur į einhverju tķmabili.
Vatn er sett ķ stóran pott og sķšan er kynt duglega undir. Vatniš er upphafleg 20°C og hitinn ķ pottinum er męldur į einnar mķnśtu fresti į mešan vatniš er aš hitna. Hitinn vex eins og taflan hér fyrir nešan sżnir.
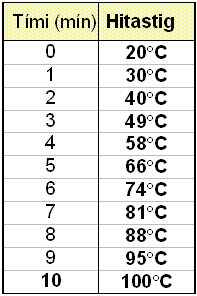
Hve hratt vex hitinn ķ pottinum?
Žaš eru margar ašferšir til žess aš tjį žetta. Viš getum t.d. fundiš mešalvaxtarhraša hitastigsins og mišaš viš hve lengi suša (100°C) var aš koma upp.
Hitinn hękkaši um 80 grįšur į 10 mķn.
Aš mešaltali hękkar hitinn um 80/10 = 8°C/mķn.
Žetta er nišurstaša sem gefur įgęta hugmynd um hve hratt hitinn vex. Ef viš hins vegar skošum tölurnar ķ töflunni sjįum viš aš hitinn vex hęgar eftir žvķ sem hitastigiš hękkar. Žaš er žvķ nįkvęmara svar aš reikna śt og gefa upp mešalvaxtarhrašann t.d. fyrstu tvęr og sķšustu tvęr mķnśturnar.
Mešalvaxtarhraši
fyrstu tvęr mķn. = (40 20)/(2 0) = 20/2 = 10°C/mķn.
sķšustu tvęr mķn. = (100 88)/(10 8) = 12/2 = 6°C/mķn.
Sżnidęmi 2
Hugsum okkur aš falliš f(x) = ¼x2 sżni einhvern tiltekinn vöxt eins og ķ sżnidęmi 1 hér fyrir ofan žar sem x er fjöldi mķnśta. Skošum žennan vöxt og byrjum į žvķ aš reikna gildistöflu.
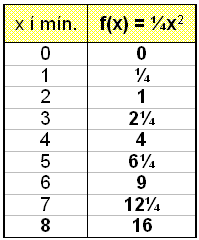
Mešalvaxtarhraši
yfir allt tķmabiliš er (16 0)/8 = 2
fyrstu tvęr mķnśturnar er (1 0)/2 = ½
sķšustu tvęr mķnśturnar er (16 9)/(8 6) = 7/2 = 3½
Viš getum einnig reiknaš mešalvaxtarhrašann um mišbik töflunnar, t.d. eftir 3 til og meš 5 mķn.
Mešalvaxtarhraši į 3. 5. mķn = (6¼ 2¼)/(5 3) = 2
Viš sjįum aš formśla fyrir mešalvaxtarhraša eftir x1 mķn. til og meš x2 veršur eftirfarandi:
|
Mešalvaxtarhraši
= |
Nś höfum viš notaš jöfnum höndum y og f(x) enda er y (eša hęš punkts į grafi) śtkoman śr formślunni f(x). Viš getum žvķ set upp formśluna fyrir mešalvaxtarhraša svona:
|
Mešalvaxtarhraši
= |
Žetta er nįkvęmlega formślan fyrir hallatölu eins og viš höfum kynnst margoft įšur žannig aš žetta er ekkert annaš en hallatala lķnu sem sker viškomandi męlipunkta į grafi f(x). Meš öšrum oršum žį er mešalvaxtarhraši hallatala snišils sem sker viškomandi męlipunkta.
Grafiš hér fyrir nešan sżnir tvo af žessum snišlum, ķ fyrsta lagi žann sem į viš allt tķmabiliš og ķ öšru lagi žann sem į viš fyrstu tvęr mķnśturnar. Jöfnur snišlanna eru fundnar žannig aš hallatalan er viškomandi mešalvaxtarhraši og punkthnitin eru tekin śr töflunni. Sķšan er sett inn ķ skuršhallajöfnuna y = k(x x1) + y1.
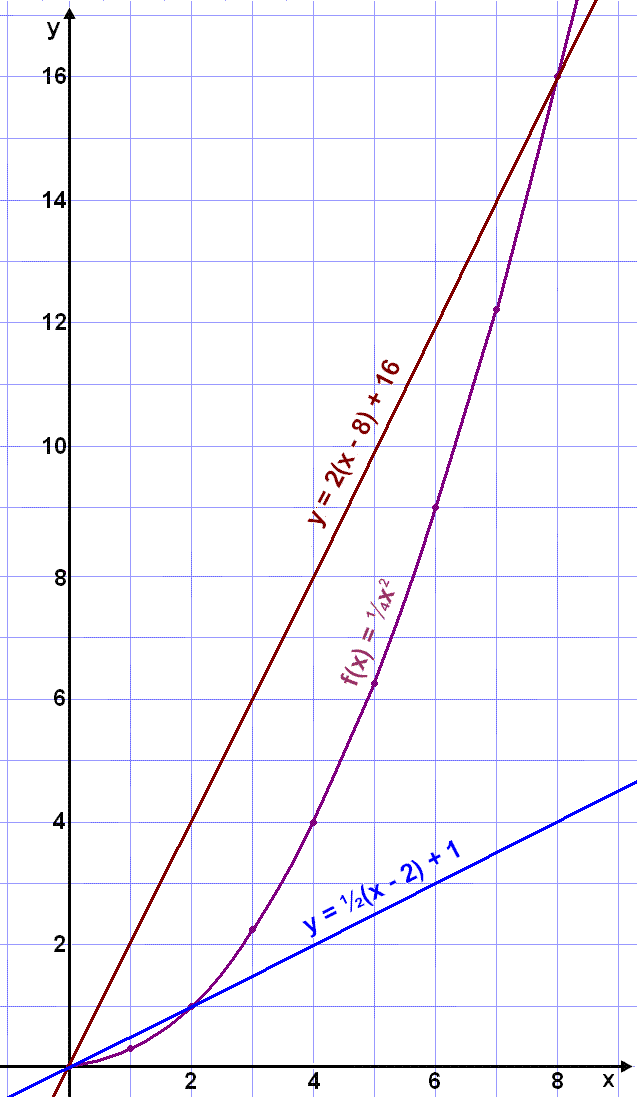
|
Mešalvaxtarhraši į bilinu x1 ≤ x ≤ x2 er
|
Finnum mešalvaxtarhraša fyrir f(x) = x3 į bilinu 2 ≤ x ≤ 2.
Reiknum fyrst śt punktana.
x1 = 2 og f(2) = (2)3 = 8
x2 = 2 og f(2) = 23 = 8
Mešalvaxtarhrašinn er
![]()
Skošum nś aftur falliš f(x) = ¼x2. Finnum mešalvaxtarhrašann ķ grennd viš x = 4. Byrjum frį vinstri og minnkum fjarlęgšina frį 4 ķ nokkrum skrefum (sjį gildistöflu ķ sżnidęmi 2).
Mešalvaxtarhraši į bilinu 1 ≤ x ≤ 4 er (4 ¼)/(4 1) = 1¼
Mešalvaxtarhraši į bilinu 2 ≤ x ≤ 4 er (4 1)/(4 2) = 1½
Mešalvaxtarhraši į bilinu 3 ≤ x ≤ 4 er (4 2¼)/(4 3) = 1¾
Myndin hér fyrir nešan sżnir snišla sem samsvara žessum śtreikningum.
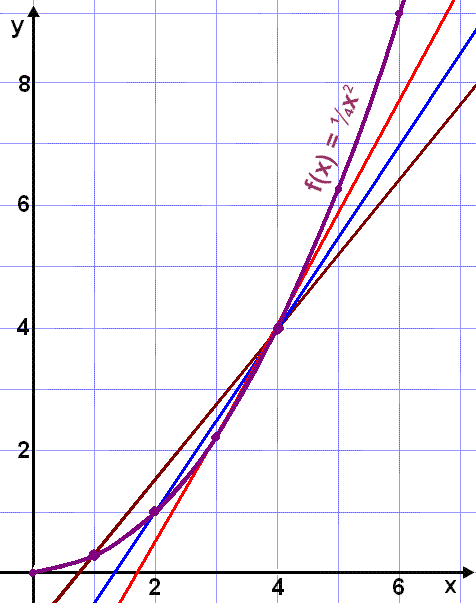
Viš fįum vönd af snišlum sem rķsa meir og meir eftir žvķ sem viš žrengjum biliš. En nś skulum viš nįlgast žetta frį hęgri.
Mešalvaxtarhraši į bilinu 4 ≤ x ≤ 7 er ( 12¼ 4)/(7 4) = 2¾
Mešalvaxtarhraši į bilinu 4 ≤ x ≤ 6 er (9 4)/(6 4) = 2½
Mešalvaxtarhraši į bilinu 4 ≤ x ≤ 6 er (6¼ 4)/(6 5) = 2¼
Af žessu sjįum viš aš mešalvaxtarhrašinn ķ grennd viš x = 4 er į bilinu 1¾ til 2¼.
Nś skulum viš finna hver mešalvaxtarhraši f(x) = ¼x2 veršur į öržröngu bili viš x = 4. Viš skulum velja punkt rétt ofan viš x = 4 eša ķ 4 + h žar sem h er lķtil tala nįlęgt nślli. Viš getum žį reiknaš mešalvaxtarhrašann į bili meš breiddina h.
Hugsum okkur myndina hér fyrir nešan vera stękkun af hluta grafsins f(x) = ¼x2 ķ grennd viš punktinn (4, 4). Snišill er dreginn ķ gegnum punktana (4, 4) og (4+h, f(4+h)).
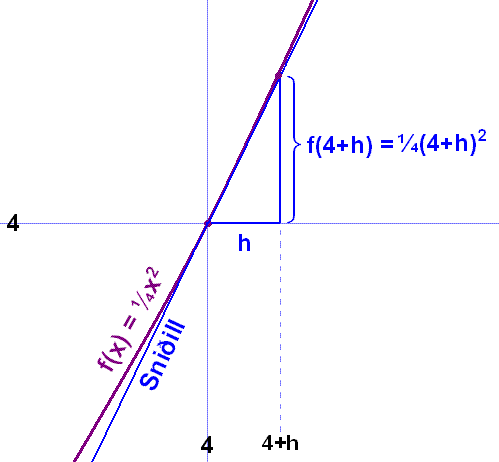
Nś er f(4+h) = ¼(4 + h)2 = ¼(16 + 8h + h2) = 4 + 2h + ¼ h2.
Snišillinn sker žvķ punktana (4, 4) og (4+h, 4+2h+¼h2) og mešalvaxtarhrašinn veršur
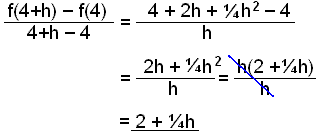
Nś getum viš vališ örlķtiš h, t.d. h = 0,04.
Žaš gefur mešalvaxtarhrašann 2 + ¼·0,04 = 2,01.
Og viš getum vališ enn žrengra bil t.d.h = 0,0004.
Žaš gefur mešalvaxtarhrašann 2 + ¼·0,0004 = 2,0001.
Žannig getum viš vališ eins žröngt bil og viš viljum og žvķ žrengra sem biliš veršur žvķ meir nįlgast mešalvaxtarhrašinn 2
enda er ![]()
Žetta markgildi gefur okkur vaxtarhrašann ķ punktinum (4, 4). Lķna sem dreginn er į sama hįtt og snišillinn į myndinni hér fyrir ofan sker ķ žessu tilfelli ašeins einn punkt og er žvķ snertill meš hallatölu sem samsvarar vaxtarhrašanum ķ punktinum (4, 4).
Ef viš setjum žessar nišurstöšur inn ķ skuršhallajöfnu lķnu fįum viš jöfnu snertilsins ķ punktinum.
y = 2(x 4) + 4 = 2x 8 + 4 = 2x 4
y = 2x 4
|
Halli snertils ķ punktinum (a, b) er
Jafna snertils ķ punktinum (a, b) er y = k(x a) + b |
Reiknum fyrst hallann.
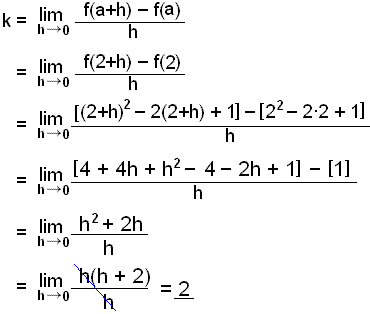 |
Fyrri hornklofarnir afmarka f(2+h) en aftari hornklofarnir afmarka f(2).
|
Jafna snertilsins veršur žį
y = 2(x 2) + 1
= 2x 4 + 1
y = 2x 3
Skošum žessa nišurstöšu į grafi śr grafķskri CASIO-reiknivél.
 |
 |
Setjum upp föllin.

Grafiš veršur eftirfarandi:
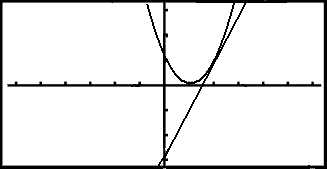
Lķnan og snertillinn snertast greinilega ķ (2, 1) žannig aš jafna snertilsins hlżtur aš vera rétt.
Žaš er einnig hęgt aš lįta reiknivélina finna hallatölu snertilsins.
Viš veljum RUN og sķšan takka sem merktur er OPTN og er viš hlišina į SHIFT-takkanum.
|
|
 |
|
 |
||
Nęst veljum viš CALC meš F4 og d/dx meš F2, en d/dx tįknar mešalvaxtarhraša į mjög litlu bili (ķ sumum bókum er žetta tįknaš meš dy/dx). Sķšan skrifum viš inn falliš og x-hnit punktsins sem viš viljum finna hallann ķ og žetta ašgreinum viš meš kommu eins og myndin hér fyrir nešan sżnir.
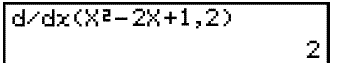
Nišurstašan veršur 2 eins og vęnta mįtti.
Ęfšu žig į žessum ašferšum og taktu sķšan próf
1 ķ afleišum.
ps. mundu eftir aš fylla śt ķ tékklistann žinn jafnóšum