© 2008 Rasmus ehf og Jóhann Ísak
|
© 2008 Rasmus ehf og Jóhann Ísak |
Afleiğur |
|
Afleiğur margliğa
Halli snertla er augljóslega mjög breytilegur eftir stağsetningu snertipunktsins. Graf falls er háğ stærğfræğilegu samhengi eğa formúlu (sem viğ oftast köllum f(x)). Halli snertils viğ grafiğ hlıtur şá einnig ağ vera háğur einhverju stærğfræğilegu samhengi eğa formúlu ef falliğ er samfellt.
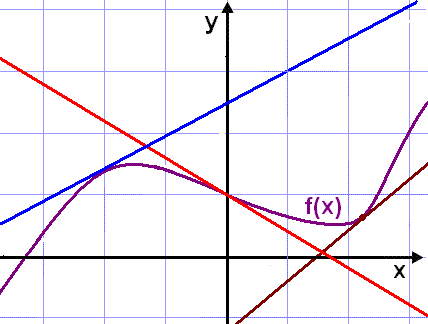
Á myndinni hér fyrir ofan eru dregnir şrír snertlar í mismunandi litum. Taktu eftir şví ağ rauğa línan sker grafiğ f(x) í einum punkti (0,1). Hallinn şar er meğalvaxtarhrağinn á örşröngu bili um (0, 1) líkt og gildir um hina snertlana. Snertlarnir hafa augljóslega mismunandi halla allt eftir şví hvar á ferli f(x) snertipunkturinn er. Viğ skulum nú athuga hvort ekki er hægt ağ finna almenna formúlu eğa fall af x sem sınir hallann hvar sem er á ferlinum. Slík föll nefnast afleiğur og eru jafnan auğkennd meğ kommu. Şannig er fall sem sınir halla snertils viğ grafiğ f(x) miğağ viğ breytileg x auğkennt f´(x) eğa y´ (einnig er notağ dy/dx).
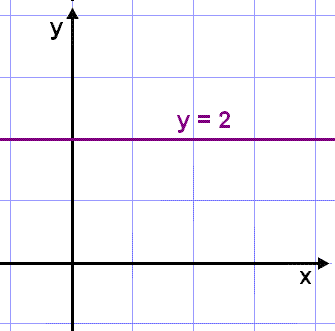
Skoğum fyrst fastafalliğ, eğa f(x) = k şar sem k er fasti (föst stærğ). Tökum sem dæmi falliğ f(x) = 2. Myndin til vinstri hér fyrir neğan sınir grafiğ.
 |
 |
Ljóst er ağ snertill viğ beina línu fellur saman viğ línuna sjálfa. Afleiğa línulegra falla er şví hallatala hennar. Hallatala láréttrar línu er 0 şannig ağ viğ getum sagt ağ ef f(x) = 2 şá er f´(x) = 0. Şetta gildir fyrir öll fastaföll şannig ağ ef f(x) = k şá er f´(x) = 0.
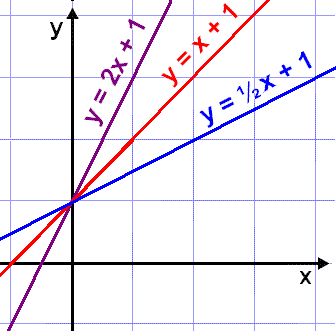
Á myndinni eru şrjár línur meğ mismunandi hallatölur. Afleiğur şeirra verğa eftirfarandi:
y = 2x + 1 hefur afleiğuna y´
= 2
y = x + 1 hefur afleiğuna y´ = 1
y = ½x + 1 hefur afleiğuna y´ = ½
Línuleg föll á forminu f(x) = ax + b hafa afleiğuna f´(x) = a.
Skoğum næst falliğ f(x) = x2.
Reynum ağ leysa markgildiğ ![]() án şess ağ binda okkur viğ fastan punkt.
án şess ağ binda okkur viğ fastan punkt.
|
Fyrir afleiğur gildir eftirfarandi almenn
skilgreining:
|
Leysum şetta markgildi fyrir f(x) = x2.
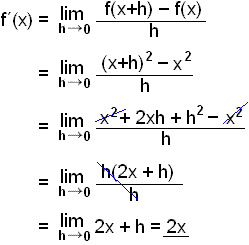 |
Şegar viğ finnum f(x+h) şá setjum viğ (x+h) í stağ breytunnar x í fallinu |
Finnum afleiğu fallsins f(x) = 2x2 + 4x.
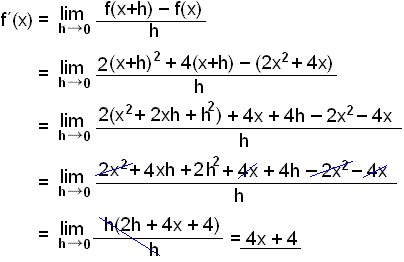
Taktu eftir şví ağ 2·x2
hefur afleiğuna 2·2x en viğ fengum hér framar ağ afleiğa x2 er 2x. Línan y = 4x hefur hallatöluna 4 şannig ağ
4x hefur afleiğuna 4. Viğ getum síğan lagt şetta tvennt saman şannig ağ
afleiğa 2x2 + 4x verğur
4x + 4. Viğ getum sett fram eftirfarandi reglu:
|
f(x) = ax2 + bx + c hefur afleiğuna f´(x) = 2ax + b. |
Finnum afleiğu fallsins ![]() .
.
Viğ höfum kynnst şví ağ ef fall er margfaldağ meğ tölu şá verğur afleiğan margfölduğ meğ sömu tölu. Nefnari brotsins virkar á sama hátt eğa eins og ağ margfalda alla liği teljarans meğ ½. Şegar nefnarinn er föst stærğ (fasti) şá getum viğ látiğ hann standa. Taktu eftir şví ağ ¼ hefur afleiğuna 0 eins og hver annar fasti.
![]()
Şetta brot getum viğ stytt.
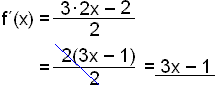
Finnum afleiğuna af f(x) = x3.
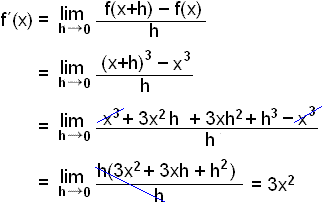
Finnum afleiğuna af f(x) = x4.
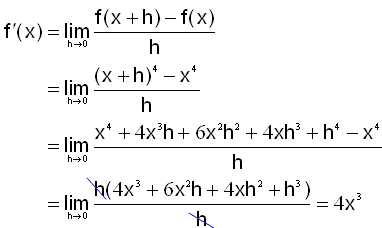
Sınidæmin hér fyrir ofan sına ákveğna reglu.
f(x) = x0
hefur afleiğuna f´(x) = 0
f(x) = x1 hefur afleiğuna f´(x) = 1·x0
f(x) = x2 hefur afleiğuna f´(x) = 2·x1
f(x) = x3 hefur afleiğuna f´(x) = 3·x2
f(x) = x4 hefur afleiğuna f´(x) = 4·x3
Şağ er engu líkara en ağ veldisvísirinn hafi veriğ færğur fram fyrir breytuna og veldiğ lækkağ um einn. Sına má fram á ağ eftirfarandi regla gildir:
|
f(x) = x n hefur afleiğuna f´(x) = n·x n1 |
Finnum afleiğu margliğunnar f(x) = x5 2x4 + 3x3 4x2 + 5x 6.
f´(x) = 5x4
2·4x3 + 3·3x2
4·2x + 5 0
= 5x4 8x3 + 9x2 8x + 5
Finnum jöfnu snertils viğ grafiğ f(x) = x5 5x3 + 4x í x = 1.
Byrjum á şví ağ finna y-hnit snertipunktsins.
f(1) = 1 5 + 4 = 0
Snertipunkturinn er (1, 0).
Finnum næst afleiğuna.
f´(x) = 5x4 5·3x2 + 4
= 5x4 15x2 + 4
Afleiğa er formúla fyrir halla şannig ağ nú getum viğ fundiğ hallatölu snertilsins sem er f´(1).
f´(1) = 5 15 + 4 = 6
Nú setjum viğ inn í skurğhallajöfnu línu.
y = 6(x 1) + 0
y = 6x + 6

|
Ağ lokum skulum viğ skoğa
grafiğ í grafískri reiknivél. |
|
|
|
Jafna snertils í punktinum (a, f(a)) er y = f´(a)(x - a) + f(a) |
Æfğu şig á şessum ağferğum og taktu síğan próf
2 í afleiğum.
ps. mundu eftir ağ fylla út í tékklistann şinn jafnóğum