© 2008 Rasmus ehf og Jóhann Ķsak
|
© 2008 Rasmus ehf og Jóhann Ķsak |
Afleišur |
|
Afleišur vķsisfalla og hornafalla
 |
Viš skulum nś
nota grafķska CASIO-reiknivél til žess aš finna nokkur gildi į föllum
af geršinni f(x) = ax
og tilsvarandi gildi į afleišunni f“(x) fyrir x = 2. Viš notum
reiknivélina til žess aš finna afleišuna meš žvķ aš velja RUN og
sķšan takka sem merktur er OPTN og er viš hlišina į SHIFT-takkanum.
Nęst veljum viš CALC meš F4 og d/dx meš F2. Loks skrifum viš inn
falliš og x-hnitiš 2. |
|
|
 |
|
 |
||
Nišurstašan veršur eins og taflan hér fyrir nešan sżnir.
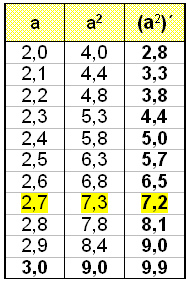
Viš sjįum aš tölurnar meš gildunum a2 vaxa frį 4 upp ķ 9 į mešan afleišurnar vaxa frį um 2,8 upp ķ um 9,9 (bįšar tölurnar eru nįmundagildi). Viš sjįum af žessu aš einhversstašar į bilinu 2 til 3 er til tala žar sem fallgildiš er jafnt afleišunni. Ķ a = 2,7 eru gildi fallsins og afleišunnar nįlęgt žvķ aš vera jöfn (7,3 og 7,2) og ef viš veljum a = 2,718282 žį fįum viš fallgildiš og afleišuna eins upp aš sjöunda aukastaf (7,3890570 og 7,3890575). Talan sem hefur nįkvęmlega sama fallgildi og afleišu er gamall kunningi. Žaš er talan e.
Talan e er óręš tala žannig aš viš getum ekki skrifaša hana nįkvęmlega en e ≈ 2,718282 og falliš f(x) = ex hefur eftirfarandi sérstaka eiginleika:
|
Falliš f(x) = ex hefur hefur afleišuna f“(x) = ex |
Viš skulum nś skoša reglu sem kallast klemmuregla. Hśn er ķ raun įkvešin ašferš til žess aš henda reišur į torleystum markgildum. Ef okkur tekst ekki aš reikna markgildi falls f(x) ķ telteknum punkti P žį getum viš reynt aš finna fall u(x) sem viš getum sżnt fram į aš skeri punktinn P en er žar fyrir utan alltaf fyrir ofan f(x). Į sama hįtt žurfum viš aš finna fall v(x) sem viš getum sżnt fram į aš skeri punktinn P og er alltaf nešan viš v(x). Ef okkur tekst aš finna markgildi u(x) og v(x) žegar stefnt er į P frį hęgri og vinstri žį höfum viš jafnframt fundiš markgildi f(x) ķ punktinum. Žessi hugsun er sżnd į myndinni hér fyrir nešan.
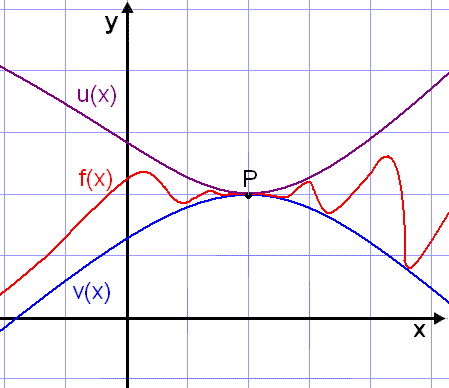
Viš skulum nś nota klemmuregluna til žess aš
finna markgildiš 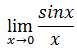 .
Vandamįliš
er aš ef viš setjum 0 inn fyrir x-iš žį
.
Vandamįliš
er aš ef viš setjum 0 inn fyrir x-iš žį
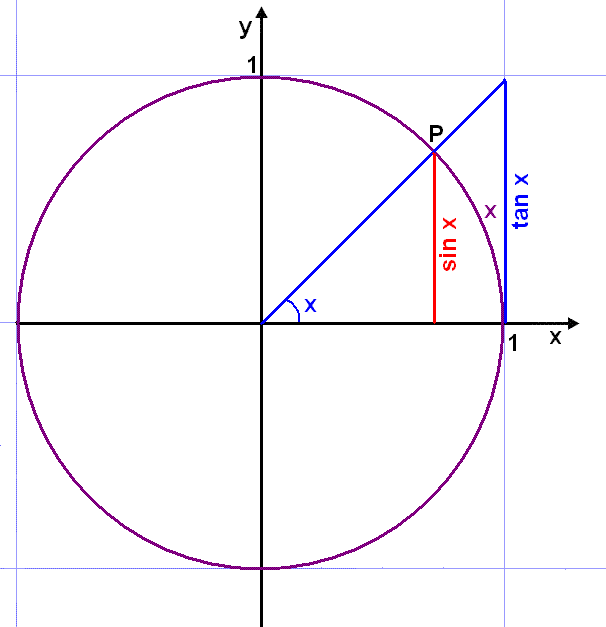
Myndin hér fyrir ofan sżnir einingarhring. Ķ hann er teiknaš horniš x. Męlt ķ bogmįli er žetta horn jafnt lengd bogans x (frį (1, 0) į x-įsnum upp aš P). Ljóst er aš sin x er styttra en boginn sem er styttri en tan x. Žar af leišandi gildir eftirfarandi ójafna:
sin
x ![]() x
x
![]() tan x
tan x
Rifjum upp skilgreininguna į tan x en hśn er
![]() .
.
![]()
Deilum ķ gegn meš sin x og styttum.
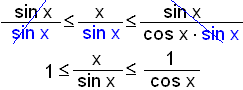
Ef žessum brotastrikum er nś velt viš žį breytist stęršarröšin og viš veršum aš snśa ójöfnunni. Hśn veršur žį eftirfarandi.
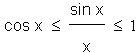
Nś höfum viš klemmt brotiš
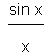 į milli 1 og
cos x og žegar x
į milli 1 og
cos x og žegar x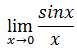 getum viš lįtiš duga aš reikna
getum viš lįtiš duga aš reikna ![]()
og žį
er ekkert til fyrirstöšu aš setja nślliš beint inn
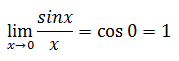
Žessa nišurstöšu getum viš notaš ķ framhaldinu.
|
|
Skošum nś annaš markgildi sem er ![]() .
.
Hér žurfum viš ekki aš nota klemmuregluna vegna žess aš viš getum margfaldaš fyrir ofan og nešan meš (cos x + 1) og nżtt okkur samokaregluna (a + b)(a b) = a2 b2.
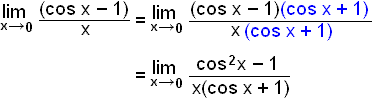
Nś munum viš eftir reglu Pżžagórasar fyrir cos og sin. Hśn var cos2x + sin2x = 1 sem mį umrita yfir į formiš sin2x = cos2x 1. Framhaldiš getur žvķ oršiš eftirfarandi:
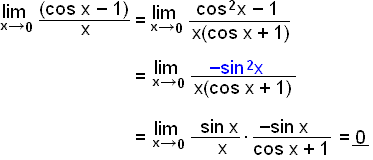
Fyrri hluti markgildisins er 1 eins og reglan hér fyrir ofan segir en seinni hlutinn og žar meš allt markgildiš et nśll vegna žess aš sin 0 = 0.
Viš skulum nś finna afleišu sin x.
![]()
Nś žurfum viš aš
rifja upp reglu śr hornafręšinni yfir sinus af summu horna sem er
sin(u +
v) = sin
u cos
v + cos
u sin
v. Setjum žetta inn ķ markgildiš hér
fyrir ofan.
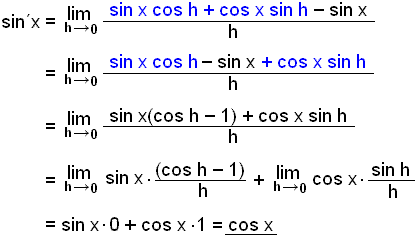
Samkvęmt reglunum hér fyrir framar žį veršur fyrri lišurinn ķ markgildinu 0 en seinni lišurinn cos x žannig aš śtkoman veršur cos x.
Į svipašan hįtt getum viš fundiš śt aš afleiša cos x er sin x.
|
sin“x = cos x cos“x = - sin x |
Finnum afleišu fallsins f(x) = tan x.
Rifjum upp aš ![]() og notum sķšan regluna
og notum sķšan regluna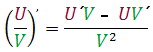 .
Žį höfum viš
u
= sin x og
u“
= cos x og einnig
.
Žį höfum viš
u
= sin x og
u“
= cos x og einnig
Žessu skulum viš raša inn ķ regluna.
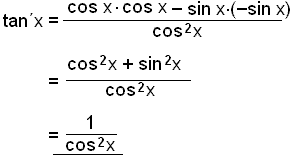 |
Hér notum viš regluna |
|
|
Finnum afleišu f(x) = ex·sin x + ex·cos x.
Byrjum į žvķ aš taka ex śt fyrir sviga til žess aš einfalda dęmiš.
f(x) = ex(sin x + cos x)
Notum nś regluna (uv)“= u“v + uv“. Viš köllum u = ex og žar meš er u“ = ex og loks köllum viš v = sin x + cos x og žį er v“ = cos x sin x. Röšum žessu nś inn ķ regluna.
f“(x) = ex(sin x + cos x) + ex(cos x sin x)
= ex sin x + ex cos x + ex cos x ex sin x
= 2ex cos x
Ęfšu žig į žessum ašferšum og taktu sķšan próf
4 ķ afleišum.
ps. mundu eftir aš fylla śt ķ tékklistann žinn jafnóšum