© 2008 Rasmus ehf og Jóhann Ķsak
|
© 2008 Rasmus ehf og Jóhann Ķsak |
Heildun |
|
Stofnföll og heildi
Heildun er notuš ķ margs konar vķsindum. Aš heilda merkir aš safna saman einhverju sem viš žaš myndar heild, eša heildi eins og žaš er kallaš, sem oftast er žį ein įkvešin tala. Heildun er m.a. notuš til žess aš reikna flatarmįl svęša sem afmarkast af gröfum falla.
Finnum flatarmįl svęšisins sem afmarkast af x-įsnum og grafi fleygbogans f(x) = x2 + 5x 4. Gerum žetta žannig aš viš teiknum sślur inn ķ grafinu, reiknum flatarmįl žeirra og leggjum loks saman.
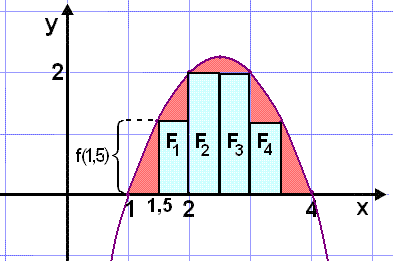
Blįu sślurnar į myndinni eru 0,5 eininga breišar og hęšin ręšst af fallinu.
Fyrsta sślan byrjar ķ x = 1,5.
Hęš hennar er f(1,5) = 1,52 + 5·1,5 4 = 1,25.
Flatarmįl hennar er F1 = 1,25·0,5 = 0,625.
Nęsta sśla byrjar ķ x = 2.
Hęš hennar er f(2) = 22 + 5·2 4 = 2.
Flatarmįl hennar er F2 = 2·0,5 = 1.
Į sama hįtt fįum viš flatarmįl hinna sślnanna, F3 = 0,625 og F4 = 0.
Samanlagt flatarmįl sślnanna veršur 0,625 + 1 + 1 + 0,625 = 3,325.
Viš sjįum aš žetta er afar ónįkvęm nįlgun į
flatarmįli svęšisins undir grafinu. Svęšiš sem litaš er rautt veršur śtundan.
Viš skulum žvķ endurbęta ašferšina meš žvķ aš žétta sślurnar.
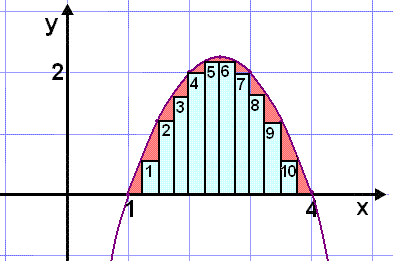 |
 |
|
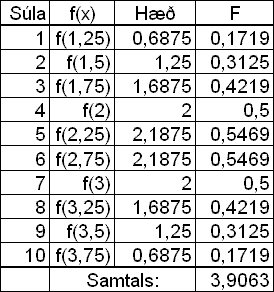
Śtreikninga į flatarmįlinu er upplagt aš gera ķ töflureikni en taflan hér til hlišar er žannig til komin. Dįlkurinn f(x) sżnir hvaša fallgildi eru notuš. |
Samtals er flatarmįl sślnanna nś 3,9063 hnitakerfisreitir sem er
greinilega réttari nišurstaša en hin
fyrri enda er rauša svęšiš į myndinni nś talsvert minna.
Viš getum ķ sjįlfu sér haldiš įfram aš žétta sślurnar į žennan hįtt en
nišurstašan veršur alltaf undir rétta flatarmįlinu,
enda er svona summa flatarmįla sślna undir grafi nefnd undirsumma.
Finnum flatarmįl svęšisins sem afmarkast af x-įsnum og grafi fleygbogans f(x) = x2 + 5x 4. Gerum žetta meš žvķ aš teikna sślur sem nį upp fyrir grafiš, reikna flatarmįl žeirra og leggja saman.
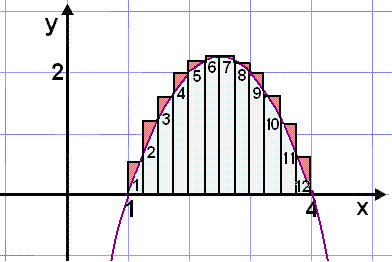 |
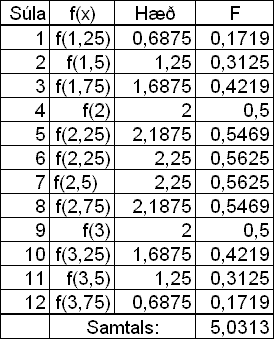 |
Dįlkurinn f(x) sżnir hvaša fallgildi eru notuš til aš reikna hęšir sślnanna en grunnlķnan er 0,25. Nišurstašan veršur 5,0313 sem er talsvert hęrri nišustaša en ķ sżnidęmi 1 og vęntanlega dįlķtiš yfir réttri nišurstöšu enda nį allar sślurnar dįlķtiš upp fyrir grafiš eins og raušlitušu hornin sżna og summa flatarmįlanna er nefnd yfirsumma. Sem fyrr getum viš žétt žétt sślurnar en nišurstašan veršur alltaf yfir réttu flatarmįli.
Nįkvęmari nišurstöšu mį einnig fį meš žvķ aš taka mešaltal af undirsummunni śr sżnidęmi 1 og yfirsummunni śr sżnidęmi 2. Žaš gefur eftirfarandi nišurstöšu:
F ≈ (3,9063 + 5,0313)/2 ≈ 4,469
Einhvers stašar į milli undirsummu og yfirsummu er hiš rétta flatarmįl undir ferlinum f(x) = x2 + 5x 4.
Žetta flatarmįl nefnist įkvešiš heildi og er tįknaš meš teygšu s-i, sem minnir į aš hér er um summu aš ręša. Ofan og nešan viš heildunarmerkiš eru tölur sem sżna efra og nešra bil heildisins. Aftan viš heildunarmerkiš er formśla fallsins sem tįknar hęš sślna hverju sinni og sķšan er margfaldaš meš dx sem į aš tįkna öržröngt bil og stendur fyrir breidd eša grunnlķnulengd hverrar sślu. Markgildiš sem fęst žegar dx stefnir į 0 er nįkvęmlega flatarmįliš, nefnist įkvešiš heildi og er tįknaš svona:
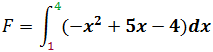
Viš getum sagt aš flatarmįliš sé įkvešna heildiš frį einum upp ķ fjóra af x2 + 5x 4.
Reiknivélar reikna įkvešin heildi į svipašan hįtt og ķ sżnidęmum 1 og 2. Margar nota trapisur ķ staš sślna eins og myndin hér fyrir nešan sżnir. Viš sjįum af myndinni aš svęšiš sem veršur śtundan (rauša svęšiš) er sįra lķtiš žó trapisurnar séu ašeins sex talsins og aušveldlega megi žétta žęr mikiš.
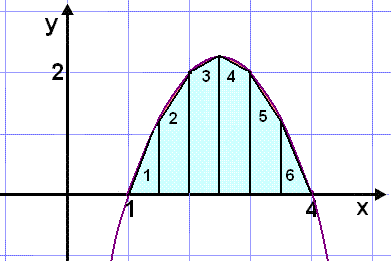
Flatarmįl trapisu er mešaltal lengdar samsķša hlišanna margfaldaš meš grunnlķnulengd eša g·(a+b)/2. T.d. er flatarmįl trapisu 2 eftirfarandi:
F = g·(a+b)/2
= 0,5·(f(1,5) + f(2))/2
= 0,5·(1,25 + 2)/2
= 0,8125
Reiknum nś flatarmįl allra trapisanna ķ töflureikni og leggjum saman.
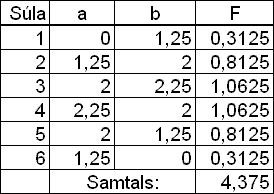
Žessi ašferš gefur nokkuš réttar nišurstöšur jafnvel meš fįum trapisum og er žvķ hentug ķ reiknitękjum. Skošum nś hvernig žetta er gert ķ grafķskri CASIO-reiknivél.
 |
 |
 |
Viš veljum RUN į ašalvalmyndinni og notum OPTN-takkann sem er viš hlišina į
SHIFT-takkanum. Sķšan veljum viš CALC meš F4 og
![]() meš F4 aftur. Viš žaš byrtist aflangt s sem er heildistįkn og opinn svigi
meš F4 aftur. Viš žaš byrtist aflangt s sem er heildistįkn og opinn svigi
![]() .
Inn ķ svigann skrifum viš falliš įsamt efri og nešri mörkum svęšisins
(heildunarinnar) sem eru ķ okkar tilfelli 1 og 4. Hér getum viš bętt viš einni
tölu ķ višbót til žess aš stilla af nįkvęmni śtreikninganna en ķ flestum
tilfellum er žaš óžarfi og viš sleppum žvķ hér. Tölurnar og formślan eru
afmarkašar meš kommu (ekki punkti) og śtkoman fęst meš žvķ aš żta į EXE į eftir
allri rommsunni.
.
Inn ķ svigann skrifum viš falliš įsamt efri og nešri mörkum svęšisins
(heildunarinnar) sem eru ķ okkar tilfelli 1 og 4. Hér getum viš bętt viš einni
tölu ķ višbót til žess aš stilla af nįkvęmni śtreikninganna en ķ flestum
tilfellum er žaš óžarfi og viš sleppum žvķ hér. Tölurnar og formślan eru
afmarkašar meš kommu (ekki punkti) og śtkoman fęst meš žvķ aš żta į EXE į eftir
allri rommsunni.
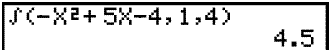
Ķ glugganum birtist śtkoman 4,5 eins og sżnt er hér fyrir ofan.
Skošum nś hvernig reikna mį įkvešin heildi nįkvęmlega įn žess aš nota reiknivélar (raunar finna reiknivélar ašeins nįlgun en eru žó jafnan mjög nįlęgt réttu svari).
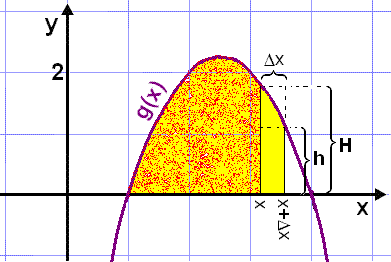
Į myndinni hér fyrir ofan höfum viš lóšrétt strik į stöšunum x og x+Δx (lesiš delta x). Biliš į milli strikanna hefur breiddina Δx en rithįtturinn Δx er mikiš notašur til žess aš tįkna mismun tveggja stęrša og žar meš breidd (žröngs) bils. Köllum flatarmįl dröfnótta svęšisins į myndinni F(x). Flatarmįl gula svęšisins (aš meštöldu žvķ dröfnótta) veršur žį F(x+Δx). Flatarmįl gula hluta sślunnar fęst meš žvķ aš taka burtu dröfnótta hluta gullitaša svęšisins. Meš öšrum oršum žį gildir eftirfarandi:
Flatarmįl gula hluta sślu er F(x+Δx) F(x).
Flatarmįl sślu įętlaš mišaš viš yfirsummu er H·Δx.
Flatarmįl sślu įętlaš mišaš viš undirsummu er h·Δx.
Flatarmįl gula hlutans er žarna į milli žannig aš eftirfarandi ójafna gildir:
h·Δx ≤ F(x+Δx) F(x) ≤ H·Δx
Deilum ķ gegn meš Δx.
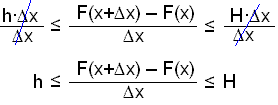
Nś er H = g(x) og h = g(x+Δx) žannig aš viš getum sett ójöfnuna upp svona.
![]()
Nś getum viš notaš
klemmuregluna og fundiš į hvaš žetta stefnir
žegar Δx
stefnir į 0.
Samkvęmt henni stefnir brotiš į g(x) žannig aš eftirfarandi markgildi veršur
nišurstašan.
![]()
Žetta rifjar upp fyrir okkur skilgreininguna į afleišu
f“(x) =
![]()
žar sem h var einmitt breidd į bili eins og Δx og ķ mörgum bókum er Δx notaš ķ staš h žegar afleiša er skilgreind.
Žetta merkir aš F“(x) = g(x) žannig aš g(x) er ķ raun afleiša flatarmįlsfallsins og flatarmįlsfalliš stofnfall g(x). Ašeins fasti ašskilur žetta tvennt. Žegar flatarmįl er reiknaš į milli tiltekinna marka žį er fyrst reiknaš upp aš efri mörkunum og sķšan nešri mörkunum. Mismunnurinn er flatarmįl bilsins og ķ frįdręttinum dettur fastinn śt og skiptir ekki mįli. Śt frį žessu mį leiša eftirfarandi reglu:
|
Įkvešiš heildi mį reikna śt frį reglunni
Óįkvešiš heildi er hins vegar įn bilmarka
og er žvķ annar rithįttur fyrir stofnfall og sį algengasti. |
Notum įkvešiš heildi til žess aš reikna flatarmįliš sem afmarkast af grafi f(x) = x2 + 5x 4 og x-įsnum.
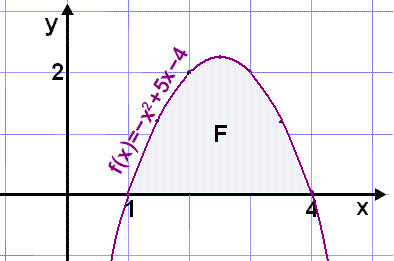
Flatarmįliš fęst meš heildun f(x) į bilinu 1 ≤ x ≤ 4. Byrjum į žvķ aš finna stofnfalliš.
|
|
Viš notum
regluna |
Reiknum nś įkvešna heildiš.
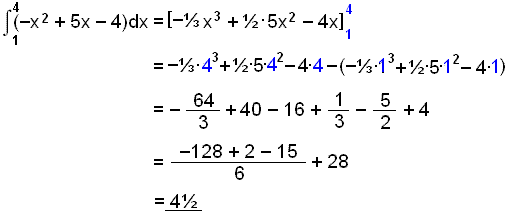
Nišurstašan er sś sama og reiknivélin fékk.
Finnum meš heildun flatarmįl svęša sem afmarkast af x-įsnum og lķnunni y = 2x 2 į bilinu 0 ≤ x ≤ 3.
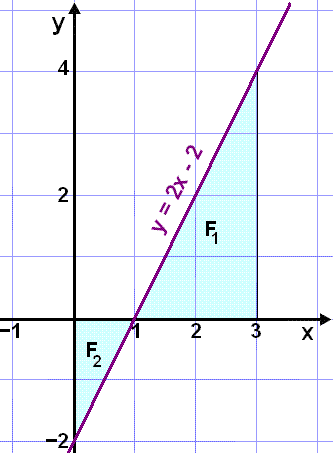
Stofnfalliš er eftirfarndi:
![]()
1) Finnum flatarmįl F1 (sjį mynd).
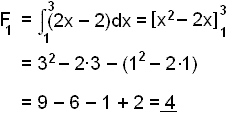
2) Finnum nęst flatarmįl F2.
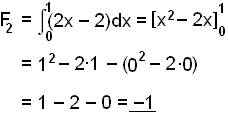
Heildi undir x-įsnum veršur greinilega neikvętt, en flatarmįl er hins vegar jįkvętt og samtals eru svęšin 5 einingar.
3) Skošum nś ![]()
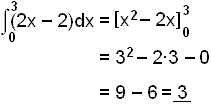
Ljóst er aš śtkoman er 4 1 = 3 og mišaš viš śtkomuna śr tveimur fyrri lišum dęmisins žį dregst flatarmįliš undir x-įsnum frį žvķ sem er fyrir ofan.
4) Athugum nś hvaš gerist ef viš heildum frį hęgri til vinstri į móti stefnu x-įssins.
Reiknum heildiš
![]()
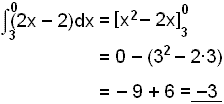
Greinilegt er aš formerki heildisins breytist ef viš heildum ķ öfuga įtt.
|
Heildi sem samsvarar flatarmįli svęšis undir x-įsnum veršur neikvętt. Ķ heildun žarf žvķ aš henda reišur į žvķ hvort graf viškomandi falls sker x-įsinn. Heildun ķ mismunandi stefnur gefur śtkomu meš mismunandi formerki (sjį regluna hér fyrir nešan).
|
Finnum flatarmįl svęšisins į milli x-įssins og sķnuskśrfunnar į
bilinu 0 til ![]() .
.
Byrjum į žvķ aš skoša grafiš ķ grafķskri reiknivél til žess aš įtta okkur į žvķ hvaša flatarmįl um ręšir.
Byrjum į žvķ aš velja GRAPH og stilla sķšan gluggann (meš V-Window). Viš skulum t.d. nota eftirfarandi gildi:
|
|
|
Skrifum sķšan inn falliš og teiknum graf.
|
|
|
Blįa svęšiš sżnir flatarmįliš sem um ręšir og viš getum fengiš žaš beint śt meš heildun.
Viš getum lįtiš reiknivélina reikna žaš eins og gert er ķ sżnidęmi 3 en viš skulum ęfa okkur į žvķ aš nota įkvešiš heildi.
Ath. Horniš ( Angle) žarf aš vera stillt į (rad).
Finnum fyrst stofnfalliš:
![]()
Įkvešna heildiš reiknum viš svona:
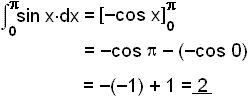
Teiknum grafiš til žess aš skoša hvaš hér um ręšir.
|
|
|
Viš žurfum greinilega aš skipta žessu ķ tvo hluta. Falliš sker x-įsinn ķ x =
![]() (cos
(cos ![]() = 0) žannig aš viš žurfum aš heilda fyrst frį 0 til
= 0) žannig aš viš žurfum aš heilda fyrst frį 0 til
![]() og ķ sķšan frį
og ķ sķšan frį ![]() til
til ![]() .
.
En byrjum į stofnfallinu.
![]()
Reiknum nś įkvešna heildiš ķ tvennu lagi.
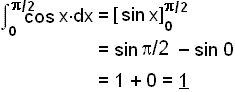
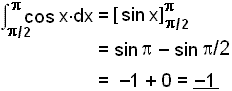
Ķ seinna tilvikinu munum viš eftir žvķ aš sleppa mķnusnum žannig aš flatarmįliš veršur samtals 2 eins og viš mįtti bśast śt frį flatarmįlinu undir sķnuskśrfunni ķ sżnidęminu hér į undan.
Finnum flatarmįl svęšisins sem afmarkast af x-įsnum og grafi f(x) = x2 3x 4.
Finnum fyrst nśllstöšvarnar. Žar eru śtmörk svęšisins.
x2 3x 4 = (x + 1)(x 4) = 0
Nśllstöšvarnar eru x = 1 og x = 4.
Skošum nś grafiš t.d. ķ grafķskri reiknivél til žess aš įtta okkur į svęšinu.
Viš byrjum į žvķ aš stilla gluggan (meš V-Window) en žaš er lķka hęgt aš gera eftir į žegar viš sjįum hvaša plįss viš žurfum.
Grafiš veršur svona:
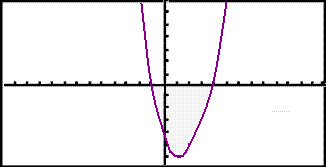
Til žess aš finna flatarmįl litaša svęšisins žurfum viš aš reikna įkvešna heildiš frį 1 til 4.
Stofnfalliš er ![]() .
.
Įkvešna heildiš veršur
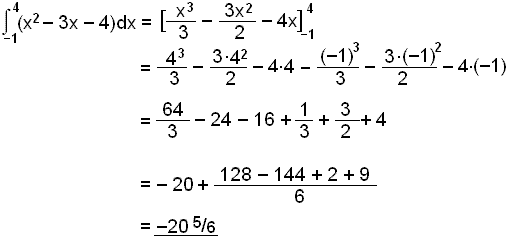
Flatarmįliš er hins vegar jįkvętt žó heildiš sé žaš ekki.
![]()
Ęfšu žig į žessum ašferšum og taktu sķšan próf
2 ķ Heildun.
ps. mundu eftir aš fylla śt ķ tékklistann žinn jafnóšum