Heildun
| © 2008 Rasmus ehf og Jóhann Ķsak |
Heildun |
|
Kynning 3
Flatarmįl svęša sem afmarkast af ferlum
Flatarmįl svęša sem gröf falla afmarka mį finna meš heildun. Skošum t.d. svęšiš
sem afmarkast af grafi fallsins f(x) = x2 + 5x 3 og lķnunni
y = x.
Žaš lķtur svona śt ķ grafķskri reiknivél:
 |
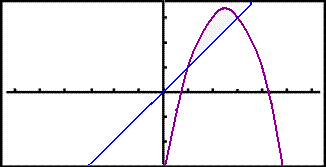 |
Til aš byrja
meš getum viš reiknaš śt hvar fleygboginn og lķnan skerast. Viš setjum
jafnašarmerki į milli jafna lķnunnar og fleygbogans
en žar er hęšin eša fallgildiš jafnt.
x2 + 5x 3 = x
x2 + 4x 3 = 0 Fęrum yfir jafnašarmerkiš.
(x2 4x + 3) = 0 Tökum 1 śt fyrir sviga.
(x 1)(x 3) = 0 Žįttum.
(x2 4x + 3) = 0
(x 1)(x 3) = 0
Skuršpunktarnir eru ķ x = 1 og x = 3. Žeir eru į lķnunni y = x žannig aš y-hnitin eru žau sömu og hnit punktanna er (1, 1) og (3, 3).
Viš getum nś fundiš flatarmįl undir ferlum meš heildun.
T.d. gefur
heildiš ![]() flatarmįlš undir
grafi
flatarmįlš undir
grafi
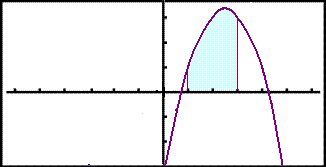
Flatarmįliš undir lķnunni y = x į bilinu 1 til 3 getum viš reiknaš
meš heildinu
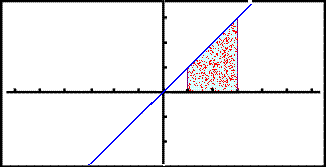
Setjum žetta nś saman ķ eina mynd.
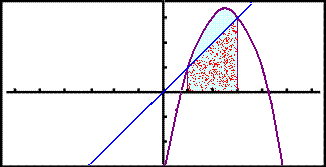
Žaš er ljóst aš
flatarmįliš į milli lķnunnar og fleygbogans fęst meš žvķ aš finna mismun
heildanna
en viš getum litiš svo į aš viš tökum dröfnótta svęšiš frį heildinni.
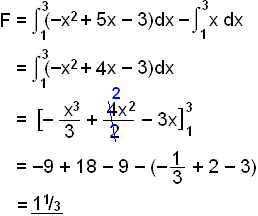 |
|
Fleygboginn fęr žį jöfnuna f(x) = x2 + 5x 3 2 = x2 + 5x 5 og lķnan jöfnuna y = x 2. Skošum grafiš ķ grafķskri reiknivél.
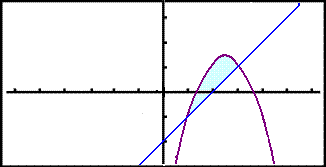
Til žess aš finna skuršpunkta fleygbogans og lķnunnar leysum viš jöfnuna fleygbogi = lķna.
x2 + 5x 5 = x 2
x2 + 4x 3 = 0 Fęrum yfir jafnašarmerkiš.
(x2 4x + 3) = 0 Tökum 1 śt fyrir sviga.
(x 1)(x 3) = 0 Žįttum.
Lausnirnar eru sem fyrr x = 1 og x = 3 žannig aš viš veršum aš heilda yfir žaš bil. Reiknum nś flatarmįliš.
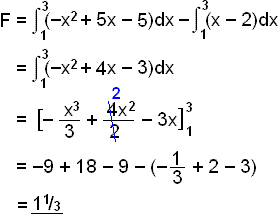
Eins og vęnta
mįtti viš fįum sama heildiš og sama flatarmįliš, enda žegar svęšiš fer nišur
fyrir x-įsinn fįum viš ķ raun tvöfaldan mķnus.
Viš žurfum žvķ ekki aš hafa įhyggjur af žvķ žó svęšiš fari nišur fyrir x-įsinn,
ašferšin gildir samt.
|
Svęši sem afmarkast af grafi f(x) aš ofan og grafi g(x) aš nešan hefur flatarmįliš
Mörkin a og b eru fundin meš žvķ aš leysa jöfnuna f(x) = g(x) sem hefur lausnirnar x = a og x = b. |
Sżnidęmi 1
Finnum flatarmįl svęšisins sem afmarkast af fleygboganum f(x) = x2 4 og lķnunni y = x 2.
Byrjum į žvķ aš leysa jöfnuna x2 4 = x 2 til žess aš finna upphaf og enda svęšisins.
x2 4 = x 2
x2 4 x + 2 = 0
x2 x 2 = 0
(x + 1)(x 2) = 0
Lausnirnar eru x = 1 og x = 2.
Skošum nś svęšiš ķ grafķskri reiknivél til žess aš įtta okkur betur į žvķ.
 |
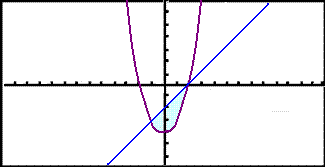 |
Viš sjįum nś aš lķnan myndar efri brśn svęšisins. Žetta merkir aš viš žurfum aš heilda lķnuna fyrst og draga sķšan heildi fleygbogans frį.
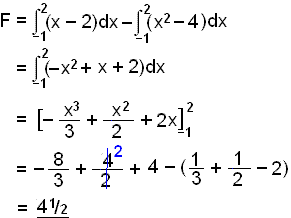
Sżnidęmi 2
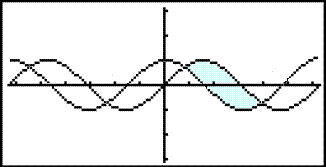
Finnum flatarįliš sem lokast af į milli grafa f(x) = sin x og g(x) = cos x į
bilinu 0 ≤ x < 2p.
Byrjum į žvķ aš skoša žetta ķ grafķskri reiknivél til aš sjį hvaš įtt er viš.
 |
 |
Hér žurfum viš aš fyrst aš finna skuršpunkta grafanna eins og jafnan ķ svona dęmum.
Leysum jöfnuna sin x = cos x.
sin x/cos x = 1 Deilum ķ gegn meš cos x
tan x = 1
x = tan1 x = p/4 + n·p
Žetta gefur lausnirnar x = p/4 og x = 5p/4 į bilinu 0 ≤ x < 2
Graf f(x) = sin x er fyrir ofan graf g(x) = cos x į öllu bilinu žannig aš flatarmįliš veršur eftirfarandi:
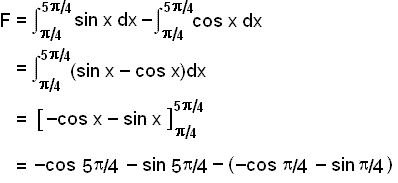
Nś er cos
p/4
= sin p/4
![]() cos 5p/4
= sin 5p/4
=
cos 5p/4
= sin 5p/4
= ![]() .
.
Flatarmįliš veršur žį
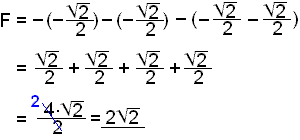
Sżnidęmi 3
Finnum flatarmįl svęšisins sem afmarkast af lķnunni y = 3x + 1 og grafi marglišunnar f(x) = ⅓ x3 2x2 + 3x + 1. Byrjum į žvķ aš skoša hvaš hér um ręšir į grafi.
Viš žurfum aš žjappa y-įsnum saman til žess aš koma žessu fyrir og stillum žvķ gluggan ķ samręmi viš žaš.
 |
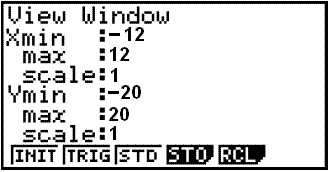 |
Grafiš birtist žį svona:
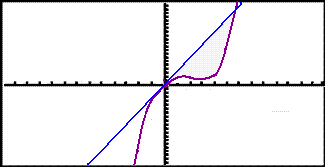
Finnum skuršpunktana.
⅓ x3 2x2 + 3x + 1 = 3x + 1
⅓ x3 2x2 = 0
x2 (⅓ x 2) = 0
Žetta gefur okkur lausnirnar x = 0 og x = 6. Viš žurfum žvķ aš heilda yfir žetta bil og lķnan myndar efrti brśn svęšisins.
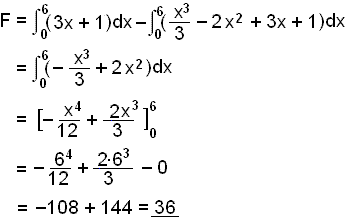
Žetta svar getum viš nś prófaš ķ reiknivélinni (meš RUN, OPTN, F4 og F4).
Ęfšu žig į žessum ašferšum og
taktu sķšan próf 3 ķ Heildun.
ps. mundu eftir aš fylla śt ķ tékklistann žinn jafnóšum