© 2008  Rasmus ehf    og Jóhann Ísak

Heildun

Kynning 4

Rúmmál snúða fundið með heildun

Hugsum okkur að við gætum snúið tilteknu grafi falls y = f(x) einn hring um x-ásinn (eða y-ásinn).
Grafið mundi þá skera út þrívíðan belg líkt og myndin hér fyrir neðan sýnir.

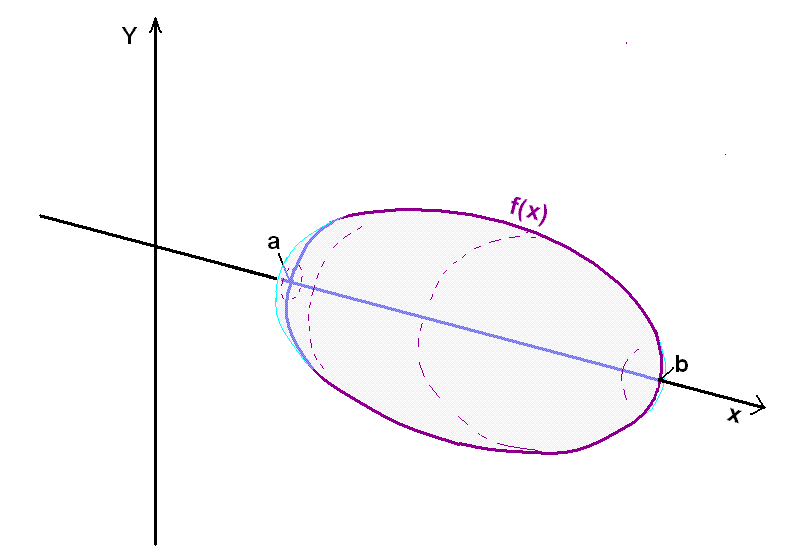
Skoðum nú hvernig við getum notað heildun til þess að reikna rúmmál svona snúðs. Þegar við fundum út hvernig við gátum notað heildun til þess að finna flatarmál undir grafi þá skiptum við svæðinu undir grafinu í örmjóar súlur sem hver um sig hafði hæðina f(x). Þegar við finnum rúmmál snúðs sem grafið f(x) sker út við snúning um heilan hring þá skiptum við snúðnum upp í örþunnar kringlóttar sneiðar eða skífur sem hver um sig hefur radíusinn f(x) (sjá næstu mynd).

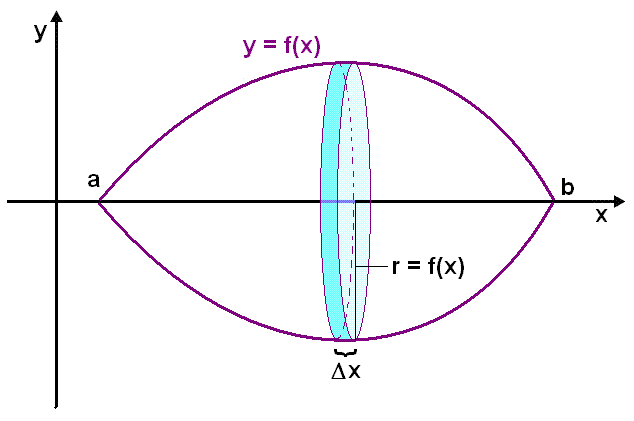
Köllum nú þykkt hverrar sneiðar x og rúmmál hverrar sneiðar R. Sneiðarnar eru í raun mjög flatir sívalningar og rúmmál sívalninga er flatarmál grunnflatar sinnum hæð eða r²·h. Hér er hæðin þykkt sneiðarinnar x þannig að rúmmál sneiðarinnar okkar verður

   R = r²·x = (fx)²x

Ef við nú heildum þessa formúlu frá a til b þá erum við í raun að leggja saman rúmmál aragrúa örþunnra sneiða. Heildi er í raun aðferð sem í þessu tilfelli finnur rúmmálið þegar fjöldi sneiða stefnir á óendanlegt og þykktin x stefnir á núll. Eftirfarandi heildi gefur okkur rúmmálið:

Fasta má taka út fyrir heildi og einfaldast er að taka út fyrir og margfalda með því síðast.

Sýnidæmi 1

Finnum rúmmál snúðsins sem myndast þegar grafi er snúið einn hring um x-ásinn.

Grafið lítur svona út í grafískri reiknivél:

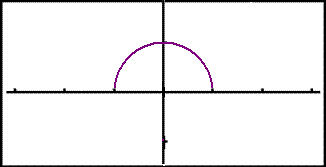Þetta er greinilega hálfhringur og þegar honum er snúið mydast kúla með radíus einn. En reiknum nú rúmmálið með heildun yfir bilið –1 ≤ x ≤ 1.

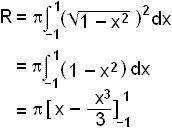
       = p(1 – ⅓ – (–1 – (–⅓)))

       = p(1 – ⅓ + 1 – ⅓)

       = 4p/3

Við skulum nú halda áfram með þetta dæmi og leysa það á almennum nótum. Skoðum hvernig dæmið liti út ef grafið sem við snérum væri graf  fallsins

. Miðað við fyrri reynslu þá er grafið hálfhringur með radíus r og sker út kúlu með radíus r ef því er snúið einn hring um x-ásinn.

Útreikningarnir verða svona:

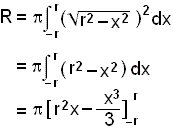
       = p(r³ – ⅓ r³ – (–r² – ⅓(–r³)))

       = p(r³ – ⅓ r³ + r³ – ⅓ r³)

       = pr³(2 – ⅔)

       = 4pr³/3

Þetta er ekkert annað en gamla góða reglan fyrir rúmmál kúlu með radíus r. Heildun er í mörgum tilvikum eifaldasta aðferðin til þess að finna rúmmálsreglur.

Sýnidæmi 2

Giftingahringur er með slétt innra byrði en kúft ytra byrði. Radíus hringsins er 8 mm miðað við innri brún og kúfurinn í mm miðast við fleygbogann f(x) = 6x – x² á bilinu 2 ≤ x ≤ 4. Finnum rúmmál hringsins.

Byrjum á því að skoða graf f(x) = 6x – x² og línunnar y = 8 en þessi tvö gröf mynda þverskurð af hringnum.

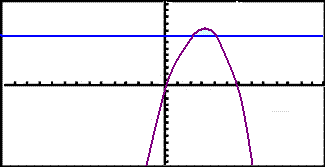Litaða svæðið sýnir þverskurð hringsins. Ef við snúum þessu svæði einn hring um x-ásinn þá fáum við allan giftingahringinn.

Fyrst þurfum við að finna skurðpunkta grafanna.

   6x – x² = 8

            0 = x² – 6x + 8

               = (x – 2)(x – 4)

Skurðpunktarnir eru x = 2 og x = 4.

Flatarmál þverskurðarins fæst með því að heilda fallið f(x) – 8 (neðra fallið er dregið frá) yfir bilið 2 ≤ x ≤ 4. Rúmmál hringsins fæst með því að snúa myndinni einn hring og formúluna yfir bilið 2 ≤ x ≤ 4.

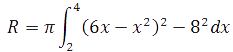
Hér þurfum við að hefja svigann í annað veldi.

   (6x – x² )²– 8² = (6x – x²)(6x – x²) – 64

                         = 36x² – 6x³ – 6x³ + x⁴

                         = x⁴ –12x³ + 36x² - 64

Rúmmálið verður þá

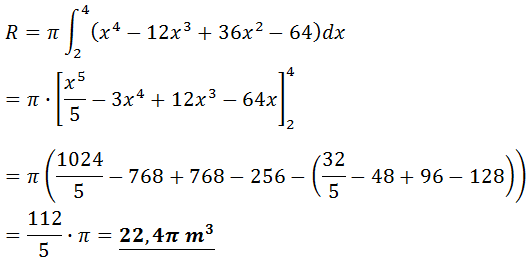
Sýnidæmi 3

Finnum rúmmál keilunnar sem myndast þegar línunni y = x er snúið einn hring um x-ásinn á bilinu x = 0 til x = 4 (sjá mynd).

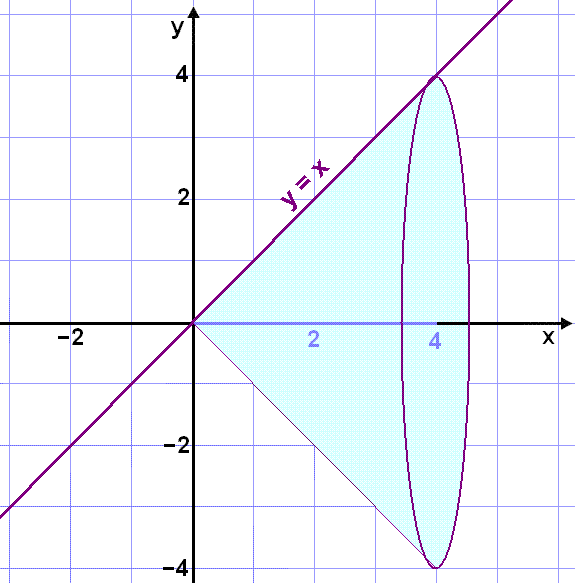
   R = ⅓ 4³ = 64/3

Það er að mörgu leyti eðlilegra að hafa keiluna í uppréttri stöðu en ekki vafða utan um x-ásinn þegar reikna á rúmmálið (sjá mynd). Þetta er fullt eins gott og stundum einfaldara, en hugsunin er önnur.

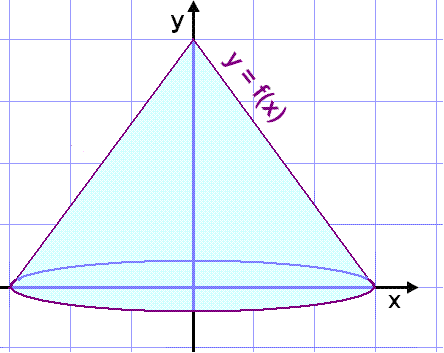
Keilan hér fyrir ofan kemur fram við það að línunni y = f(x) er snúið einn hring um y-ásinn. Hugsum okkur nú að við vildum skera þunnan hólk innan úr keilunni (sjá myndina hér fyrir neðan) og rúlla honum út.

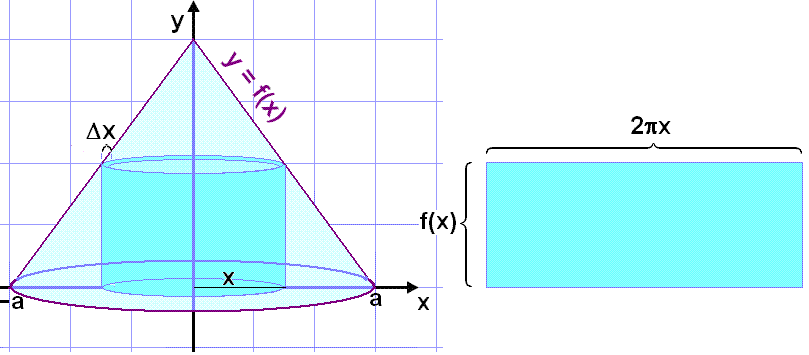
Þessi aðferð er oftast einfaldari en skífuaðferðin þegar kemur að útreikningum vegna þess að hér þurfum við ekki að hefja fallið í annað veldi og auk þess er heildað frá núlli.

Sýnidæmi 4

Finnum rúmmál bjöllunnar sem myndast ofan við x-ásinn þegar grafi fallsins f(x) = 4 – x² er snúið einn hring í kringum y-ásinn. Myndin hér fyrir neðan sýnir bjölluna.

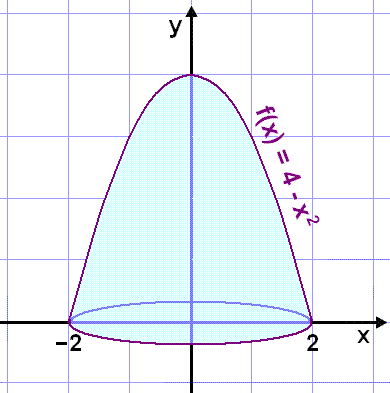
Við nýtum okkur hólkaðferðina.

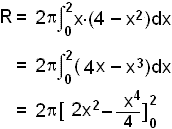
       = 2p(8 – 4) = 8p

Sýnidæmi 5

Finnum rúmmál keilunnar sem myndast þegar línunni y = 2x + 1 á bilinu 0 ≤ x ≤ 4 er snúið einn hring um y-ásinn.

Skoðum þetta fyrst á mynd.

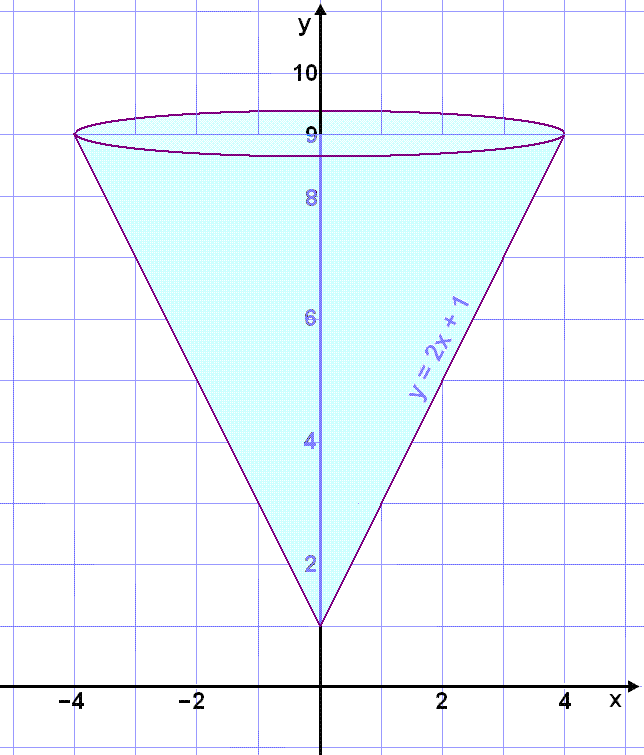
Ef við nú notum hólkaðferðina og heildum línuna áhyggjulaust frá x = 0 upp í x = 4 þá fáum við rúmtak hólkanna sem eru utan við keiluna. Eins og í flatarheildun þá verðum við að miða við efra fallið (y = 9) og draga neðra fallið (y = 2x + 1) frá. Rúmmálið verður þá eftirfarandi:

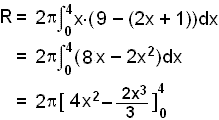
      = 2p(64 – 42⅔) = 128p/3

Sýnidæmi 6

Kúftur skermur úr gleri er fleygbogi að utan og keila að innan. Ytra byrðið fylgir ferlinum f(x) = x²/10 og innra byrðið (keilan) fylgir línunni y = x + 20 ef mælt er í cm. Reiknum rúmtak glersins.

Byrjum á því að teikna þetta upp.

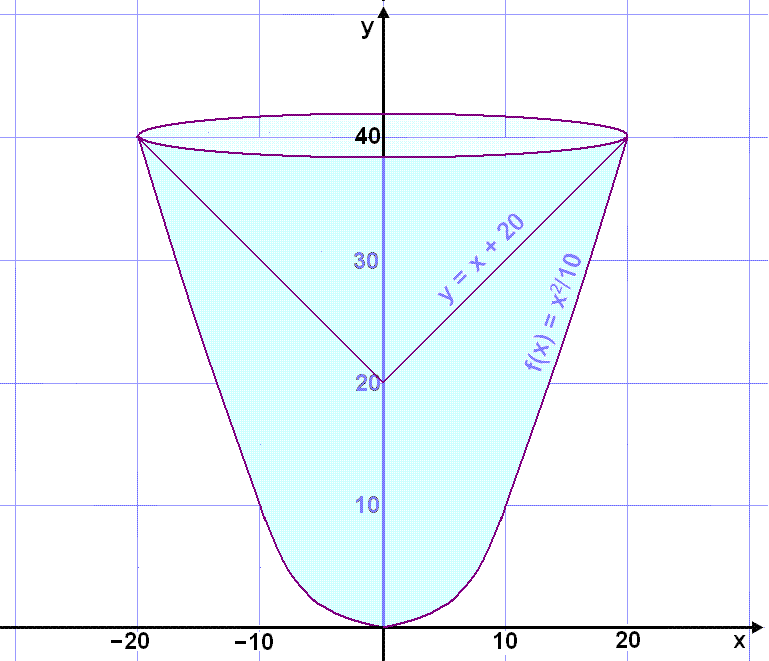
Við þurfum greinilega að nota hólkaðferðina og hólkarnir afmarkast af y = x + 20 að ofan og x²/10 að neðan sem þá dregst frá.

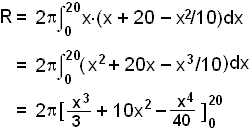
      = 2p(2666⅔ + 4000 – 4000) = 16000p/3 cm³.

Æfðu þig á þessum aðferðum og taktu síðan próf 4 í Heildun.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum