© 2008 Rasmus ehf og Jóhann Ķsak Pétursson
© 2008 Rasmus ehf og Jóhann Ķsak Pétursson |
Heildun |
|
Lišun ķ stofnbrot
Viš höfum kynnst žvķ aš stofnfall f(x) = 1/x er F(x) = ln lxl.
Skošum nś hvort žessi regla gildir fyrir öll föll af geršinni f(x) = 1/n(x) žar sem n(x) er margliša af fyrsta stigi (ax + b).
Athugum hvort
![]() = ln lx + 1l + C er rétt heildun.
= ln lx + 1l + C er rétt heildun.
Žaš gerum viš meš žvķ aš deilda stofnfalliš.
(ln lx + 1l +
C)“ =
![]() .
.
Žetta stemmir en
skošum nęst hvort žetta gildir um heildiš
![]() .
.
Gerum rįš fyrir aš stofnfalliš sé 2·ln l3x + 4l + C og deildum.
(2·ln l3x + 4l
+ C)“ =
![]() .
.
Hér margföldum viš meš afleišu innra fallsins (sem er 3) žannig aš stofnfalliš sem viš reyndum er žrisvar sinnum of hįtt. Viš hefšum įtt aš reyna stofnfalliš ⅓·2·ln l3x + 4l + C. Viš sjįum aš eftirfarandi regla gildir:
|
|
Skošum nś hvernig viš getum heildaš stęšur žar sem annars stigs margliša er undir strikinu, en fyrst žurfum viš aš rifja upp dįlķtinn brotareikning.
![]()
Samnefnarinn er 6 og nś lengjum viš brotin og gerum žau samnefnd.
![]()
2 gengur žrisvar upp ķ samnefnarann 6 žannig aš viš margföldum fyrra brotiš meš 3 bęši fyrir ofan og nešan strik.
3 gengur hins vegar tvisvar upp ķ 6 žannig aš viš lengjum seinna brotiš meš 2.
En skošum žetta meš bókstöfum.
![]()
Samnefnarinn er xy žannig aš viš lengjum fyrra brotiš meš y og seinna brotiš meš x.
![]()
Skošum fleiri og flóknari dęmi.
![]()
Samnefnarinn er (x + 2)(x + 1) žannig aš viš veršum aš lengja lišinn til vinstri meš (x + 1) og lišinn til hęgri meš (x + 2).
![]()
Reiknum žetta nś ķ hina įttina.
![]()
Viš byrjum į žvķ aš žįtta nefnarann.
x2 + 3x + 2 = (x + 2)(x + 1)
Nś getum viš sett žetta upp svona:
![]()
Ef viš ętlum aš reikna svona dęmi ķ öfuga įtt žį žurfum viš aš finna stušlana a og b. Prófum aš gera samnefnt hęgra megin viš jafnašarmerkiš.
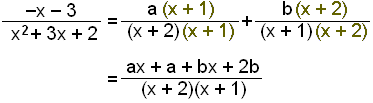
Nś vitum viš aš x-in hęgra megin (ax + bx) eru jafn mörg og vinstra megin (−x) žannig aš eftirfarandi jöfnur gilda:
ax + bx = −x sem veršur a + b = −1 ef viš deilum ķ gegn meš x.
Žį eru eftir hreinir tölulišir sem eru samtals −3.
a + 2b = −3
Nś höfum viš eftirfarandi jöfnuhneppi:
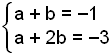
Ef viš nś leysum saman žetta jöfnuhneppi (t.d. meš žvķ aš draga efri jöfnuna frį žeirri nešri) fįum viš b = −2 og a = 1 sem er žaš sama og viš lögšum upp meš.
![]()
Žessi ašferš viš aš reikna brotasamlagningu til baka nefnist lišun ķ stofnbrot og hana mį nota ķ heildun eins og sżnidęmiš hér fyrir nešan sżnir.
En finnum nś eftirfarandi heildi:
![]() =
2∙ln
lx
+ 1l
+ C
=
2∙ln
lx
+ 1l
+ C
|
= ln (x + 1)2 + C |
Hér notum viš regluna n∙ln a = ln an |
![]() = ½∙2∙
ln
l2x + 1l
+ C = ln
l2x
+ 1l
+ C
= ½∙2∙
ln
l2x + 1l
+ C = ln
l2x
+ 1l
+ C
![]()
Nś žurfum viš aš žįtta og liša ķ stofnbrot.
x2 1 = (x + 1)(x 1)
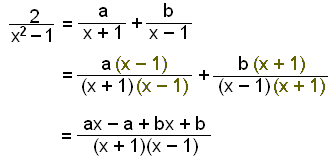
Nęst finnum viš tölurnar a og b.
X-lišur er enginn vinstra megin žannig aš ax + bx er 0.
Töluliširnir eru 2 į vinstri hliš en a + b į žeirri hęgri.
Žetta gefur eftirfarandi jöfnuhneppi:
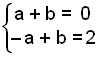
Žetta jöfnuhneppi getum viš aušveldlega leyst.
Ef viš t.d. leggjum saman jöfnurnar žį fįum viš 2b = 2.
Žannig aš b = 1 sem gefur a = −1.
Nś getum viš lišaš ķ stofnbrot og heildaš.
|
|
|
![]()
Viš byrjum į žvķ aš žįtta nefnarann.
x2 + 3x + 2 = (x + 1)(x + 2)
Sķšan lišum viš ķ stofnbrot.
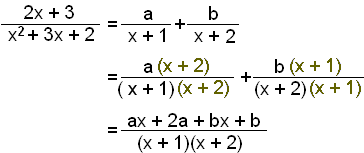
X-liširnir gefa okkur jöfnuna ax + bx = 2x eša a + b = 2.
Töluliširnir gefa jöfnuna 2a + b = 3.
Leysum žvķ jöfnuhneppiš
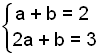
Ef viš drögum efri jöfnuna frį žeirri nešri fįum viš a = 1 og
innsetning gefur b = 1.
Nś getum viš heildaš.
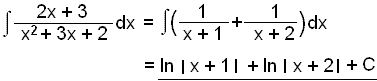
![]()
Žįttun: x2 + 3x = x(x + 3)
Lišun ķ stofnbrot:
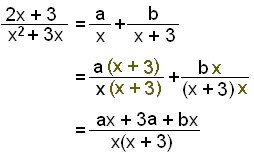
Töluliširnir gefa 3a = 3 og a = 1.
X-liširnir eru ax + bx = 2x sem gefur a + b = 2 og b = 1.
Heildunin veršur loks eftirfarandi:
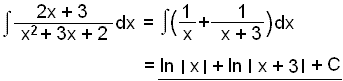
![]()
Žįttun: x3 5x2 + 4x = x(x2 5x + 4) = x(x 1)(x 4)
Lišun ķ stofnbrot:
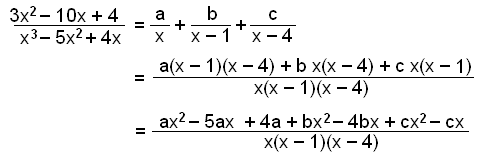
Stušlar viš x2 gefa jöfnuna ax2 + bx2 + cx2 = 3x2 og žį fįum viš a + b + c = 3.
Stušlarnir viš x gefa jöfnuna −5ax 4bx cx = −10x og
žannig fįum viš jöfnuna 5a + 4b + c = 10.
Hreinn tölustušull er ašeins 4a = 4 žannig aš a = 1.
Meš innsetningu fįum viš 1 + b + c = 3 eša b + c = 2 og
5 + 4b + c = 10 eša 4b + c = 5.
Ef viš nś drögum jöfnuna b + c = 2 frį jöfnunni 4b + c = 5
Fįum viš 3b = 3 žannig aš b = 1.
Loks fįum viš meš innsetningu 1 + c = 2 žannig aš c = 1.
Heildun:
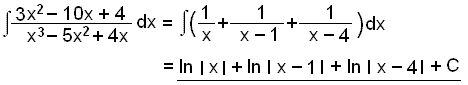
Ęfšu žig į žessum ašferšum og taktu sķšan próf
5 ķ Heildun.
ps. mundu eftir aš fylla śt ķ tékklistann žinn jafnóšum