© 2008  Rasmus ehf    og Jóhann Ísak Pétursson

Heildun

Kynning 6

Hlutheildun

Hugsum okkur tvö samfelld föll af breytunni x, föllin u(x) og v(x) sem hafa afleiðurnar u´(x) og v´(x). Til hægðarauka skulum við kalla föllin einfaldlega  u og v og afleiðurnar u´og v´.

Reglan um afleiðu margfeldis tveggja falla gefur eftirfarandi:

   (u∙v)´ = u´∙v + u∙v´

Heildum nú þessa jöfnu (sleppum breytunni x til einföldunar).

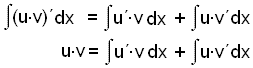
Við skulum nú snúa þessari jöfnu, en þá kemur út eftirfarandi regla:

Þessa umritun má oft nota með góðum árangri þegar heilda þarf tvö föll sem eru margfölduð saman. Á það einkum við þegar afleiðan v´(x) er einfaldari (t.d. fasti) en stofnfall þess v(x).

Notum nú þessa aðferð til þess að finna nokkur heildi.

Sýnidæmi 1

 
  Nú skulum við kalla föllin sömu nöfnum og í reglunni.

  Við setjum v = x vegna þess að afleiðan v´ verður þá fasti.

    v = x og v´ = 1

    u = e^x og u´= e^x

  Nú getum við raðað inn í regluna og heildað.

 
    v ∙ u´         u ∙ v       v´ ∙ u

                   = x∙e^x – e^x + C

Sýnidæmi 2

   
  Nú veljum við að kalla það fall v sem hefur einfaldari afleiðu.

    v = 2x + 1 og þá er v´= 2

    u´ = cos x og þá er u = sin x

  Notum nú regluna.

                              = (2x + 1) sin x + 2 cos x + C 

Sýnidæmi 3

  Við veljum

     v = x² og þá er v´ = 2x

     u´ = cos x og þá er u = sin x

  Notum regluna.

    
  Nú þurfum við að nota regluna aftur.

  Við veljum

     v = 2x og þá er v´ = 2

     u´ = sin x og þá er u = −cos x

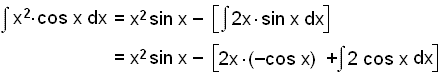
                   = x² sin x + 2x cos x − 2 sin x + C

Sýnidæmi 4

  Nú er ekkert val um v og u´.

     v = e^x = v´

     u´ = e^x = u

  Í fljótu bragði virðumst við engu nær en einmitt nú getum við snúið dæminu okkur í hag.
  Það gerum við með því að fær heildið á hægri hlið jöfnunnar yfir á vinstri hlið.
  Niðurstaðan verður eftirfarandi:

  Loks deilum við í gegn með 2.

     = ½ e^x ∙ e^x + C

  Þetta er sjálfsögð niðurstaða vegna þess að  e^x ∙ e^x  = e^2x  sem

  hefur stofnfallið  ½ e^2x + C  eins og fram hefur komið.

Sýnidæmi 5

  Sem fyrr veljum við v og u´.

        v = sin x og þá er v´ = cos x

        u´ = e^x og þá er einnig u = e^x

  Við erum nú engu nær en reynum þó að nota regluna aftur:

      v = cos x og þá er v´ = −sin x

      u´ = e^x  og þá er u = e^x

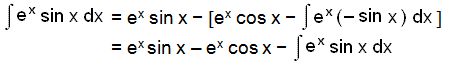
  Nú erum við komin í hring. Við erum aftur komin með e^x sin x.

  Reynum nú að færa yfir jafnaðarmerkið líkt og í dæminu hér fyrir ofan.

  Nú þurfum við bara að deila í gegn með 2.

                          = ½ e^x (sin x – cos) x + C

Sýnidæmi 6

  Hér er ekkert margfaldað saman þannig að ekki er ljóst hvernig við getum notað regluna. En við getum margfaldað með 1. Það skemmir ekkert.

  Hér er ljóst að við verðum að velja u´ = 1 (það er ekkert gagn í

  því að fá inn v = 1 og v´ = 0).

     v = ln x og þá er v´ = 1/x

     u´ = 1 og þá er u = x

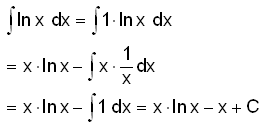
Í framhaldi af sýnidæmi 6 getum við sett fram eftirfarandi reglu:

Sýnidæmi 7

Oftast reynist best að velja v = ln x. v´verður þá 1/x sem oft má stytta út.

      v = ln x og þá er v´= 1/x

     u´ = 18x² og þá er u = 18x³/3 = 6x³

   
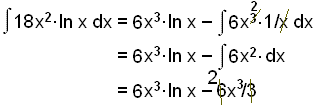
                           = 6x³∙ln x – 2x³ + C