© 2008  Rasmus ehf    og Jóhann Ísak Pétursson

Runur og raðir

Kynning 2

Kvótarunur

Jafnhlutfallarunur eða kvótarunur nefnast talnarunur þar sem sama hlutfallið helst á milli liða. Þessu má lýsa með eftirfarandi formúlu:

T.d. er hlutfallið k hálfur í eftirfarandi runu.

   100, 50, 25, 12½, 6¼, 3⅛, . . . .  

(Athugaðu að punktarnir standa fyrir o.s.frv.)

Við getum sett þetta upp svona:

a₁ = 100

a₂ = 100∙½ = 50

a₃ = 100∙(½)² = 25

a₄ = 100∙(½)³ = 12½

a₅ = 100∙(½)⁴ = 6¼

a_n = 100∙(½)^n-1

Almennt gildir eftirfarandi regla:

Sýnidæmi 1

Fyrstu tveir liðir kvótarunu eru 8 og 6. Finnum fjóra fyrstu liðina.

Finnum fyrst kvótann k.

Nú getum við reiknað liðina.

a₁ = 8

a₂ = 8∙¾ = 6

a₃ = 8∙(¾)² = 4½

   a₄ = 8∙(¾)³ = 3⅜

Sýnidæmi 2

Í kvótarunu er þriðji liðurinn 2 og fjórði liðurinn 4. Finnum fyrstu sex liðina.

Byrjum á því að finna kvótann k.

   k = 4/2 = 2

Setjum nú t.d. fjórða liðinn og k inn í regluna og finnum a₁.

   a₄ = a₁∙k³

    4 = a₁∙2³ = a₁∙8

  a₁ = 4/8 = ½

Nú getum við notað regluna beint til þess að reikna framhaldið.

   a₂ = ½∙2 = 1

   a₃ = ½∙2² = 2

   a₄ = ½∙2³ = 4

   a₅ = ½∙2⁴ = 8

   a₆ = ½∙2⁵ = 16

Sýnidæmi 3

Í kvótarunu er a₃ = 128 og a₆ = 2. Finnum sex fyrstu liðina.

Hér hefur a₃ = 128 verið margfaldað þrisvar með k og þannig hefur fengist liðurinn a₆ = 2.

   128∙k³ = 2

          k³ = 2/128 = 1/64

            = ¼

Nú getum við notað regluna til þess að finna fyrsta liðinn a₁.

      a₃ = a₁∙k²

   128 = a₁∙(¼)²

      a₁ = 128/(¼)² = 128∙16 = 2048

Notum loks regluna beint til þess að reikna liðina sem vantar.

   a₂ = 2048∙¼ = 512

   a₃ = 2048∙(¼)² = 128

   a₄ = 2048∙(¼)³ = 32

   a₅ = 2048∙(¼)⁴ = 8

   a₆ = 2048∙(¼)⁵ = 2

Sýnidæmi 4

Í kvótarunu er a₃ = 250 og a₅ = 62½. Finnum kvótann k og fjóra fyrstu liðina.

Við sjáum að 250 hefur verið margfaldað tvisvar (5 – 3 = 2) með k og útkoman er 62½.

  250∙k² = 62½

         k² = 62½/250 = ¼

          k = ½

Hér fáum við kvóta sem getur bæði verið neikvæð og jákvæð tala. Fyrstu liðina fáum við með því að deila með k.

  a₂ = 250/(½) = 500

Hér getum við ekki verið viss um formerkið en ef liðurinn er neikvæður þá er það vegna þess að k = −½ og næsta deiling gefur örugglega jákvæðan lið.

  a₁ = 500/½ = 1000

Fyrstu liðir rununnar líta þá svona út en við getum ekkert sagt til um formerki annars hvers liðar.

  a₁ = 1000

  a₂ = 500

  a₃ = 250

  a₄ = 125

Snúum okkur nú að fleiri kvótarunum sem fylgja reglunni a_n = a₁∙kⁿ⁻¹.

Skoðum dæmi.

a₁ = 12

a₂ = 3

a₃ = 0,75

a₄ = 0,1875

a₅ = 0,046875

Við finnum k = 3/12 = ¼ og við sjáum að liðirnir minnka hratt. Á grafi lítur þetta svona.

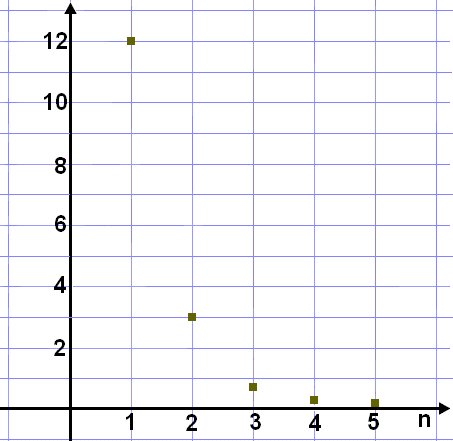
Við sjáum að liðirnir nálgast  hratt núll þegar n hækkar sem kemur fram í því að punktarnir setjast á n-ásinn.
Þetta líkist einna helst láréttum aðfellum. Runur með þessa eiginleika kallast  samleitnar runur.

Runan hér fyrir ofan er samleitin og ástæðan fyrir því að er sú að k er brot þannig að margföldun með k veldur minnkun.

Prósentubreytingar fylgja kvótarunum. Aukning um 10% samsvar breytingu frá 100 upp í 110 þannig að kvótinn í runu
prósentuhækkana þar sem hækkunin er 10% verður  k = 110/100 = 1,1. Að sama skapi samsvarar minnkun um 10%
að 100 lækkar niður í 90 þannig að kvótinn í runu prósentuminnkunar verður  k = 90/100 = 0,9.

Nú getur prósentuhækkun farið yfir 100% og þá er ekki einfalt að sjá út hver kvótinn k verður. Skoðum eftirfarandi:

      1% hækkun, k = 1,01

      5% hækkun, k = 1,05

    10% hækkun, k = 1,10

    25% hækkun, k = 1,25

    90% hækkun, k = 1,90

  100% hækkun, k = 2,00

  200% hækkun, k = 3,00

Almennt gildir:

Samskonar regla gildir fyrir prósentulækkun:

Sýnidæmi 5

Siggi keypti bíl fyrir 3.000.000 kr. Hann fékk alla upphæðina að láni afborgunarlaust í fimm ár á 10% ársvöxtum. Verðmæti bílsins rýrnar um 20% á ári.
Hve mikið kostar það Sigga að eiga bílinn í fimm ár ef aðeins er tekið tillit til verðrýrnunar og vaxta?

Lýtum fyrst á vextina.

    Upphaflegt lán, a₀ = 3.000.000 kr.

          Eftir 1. árið, a₁ = 3.000.000∙1,10 = 3.300.000 kr.
          Eftir 2. árið, a₂ = 3.300.000∙1,10 = 3.630.000 kr.
          Eftir 3. árið, a₃ = 3.630.000∙1,10 = 3.993.000 kr.
          Eftir 4. árið, a₄ = 3.993.000∙1,10 = 4.392.300 kr.
          Eftir 5. árið, a₅ = 4.392.300∙1,10 = 4.831.530 kr.

  Samtals greitt í vexti:

       4.831.530 – 3.000.000 = 1.831.530 kr.

Verðrýrnun:

  Upphaflegt verð, a₀ = 3.000.000 kr.

          Eftir 1. árið, a₁ = 3.000.000∙0,80 = 2.400.000 kr.
          Eftir 2. árið, a₂ = 2.400.000∙0,80 = 1.920.000 kr.
          Eftir 3. árið, a₃ = 1.920.000∙0,80 = 1.536.000 kr.
          Eftir 4. árið, a₄ = 1.536.000∙0,80 = 1.228.800 kr.
          Eftir 5. árið, a₅ = 1.228.800∙0,80 = 983.040 kr.

  Samtals verðrýrnun:

        3.000.000 – 983.040 = 2.016.960 kr.

 Kostnaður samtals:

        1.831.530 + 2.016.960 = 3.848.490 kr.

Við sjáum af sýnidæminu hér fyrir ofan að reglan  a_n = a₁∙kⁿ⁻¹  gildir þegar reiknaðir eru vaxtavextir,
en þá verður að gera ráð fyrir að  a₁ tákni upphæðina með vöxtum eftir fyrsta árið.
Ef við hins vegar göngum út frá upphaflegum höfuðstól (a₀) þá verður reglan eftirfarandi:

Þessi regla gildir einnig fyrir prósentuminnkun, en þá er k < 1.

Sýnidæmi 6

Sigga leggur 10.000 kr. inn í banka sem borgar 8% ársvexti. Hve há verður upphæðin eftir 10 ár?

Við notum regluna a₁₀ = a₀∙k¹⁰ þar sem a₀ = 10.000 og k = 1,08

 a₁₀ = 10.000∙1,08¹⁰ = 21.589 kr.

Sýnidæmi 7

Sigga sér að annar banki býður 10% vexti. Hve lengi er upphæð sem lögð er inn á þann reikning að tvöfaldast?

Leggjum inn eina krónu og finnum út hvenær hún er orðin að tveimur krónum.

   2 = 1∙1,10ⁿ

Hér þurfum við að grípa til logra.

   ln 2 = ln 1,1ⁿ

       n = ln 2/ln 1,1 ≈ 7,3 ár.