© 2008  Rasmus ehf    og Jóhann Ísak Pétursson

Runur og raðir

Kynning 3

Mismunaraðir

Lítum á stæðuna 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10. Svona stæða er í raun mismunaruna  (mismunur liða er 1) lögð saman. Almennt gildir að þegar runur eru lagaðar saman nefnist stæðan röð. Þegar mismunaruna er lögð saman verður stæðan mismunaröð.

Ef a₁, a₂, a₃, a₄, . . . . . . , a_n er mismunaruna þá er a₁ + a₂ + a₃ + a₄ + ∙ ∙ ∙ ∙ ∙ ∙ + a_n mismunaröð.

Nú er munur liða d þannig að við getum einnig ritað röðina svona

   a₁ + (a₁ + d) + (a₁ + 2d) + (a₁ + 3d) + ∙ ∙ ∙ ∙ ∙ ∙ + (a₁ + (n−1)d)

Við getum einnig byrjað aftan frá og dregið alltaf frá.

   a_n + (a_n − d) + (a_n − 2d) + (a_n − 3d) + ∙ ∙ ∙ ∙ ∙ ∙ + (a_n − (n−1)d)

Köllum nú summu raðarinnar S_n. Við getum fundið S_n ýmist framan frá eða aftan frá. Ef við nú leggjum saman á báða vegu þá fáum við eftirfarandi:

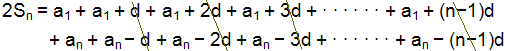
           = n∙a₁ + n∙a_n

           = n∙( a₁ + a_n)

Ef við nú deilum í gegn með 2 þá fáum við eftirfarandi reglu:

Í raun segir reglan okkur að finna meðaltal fyrsta og síðasta liðs. Þá höfum við fundið tölu sem við getum litið á sem fulltrúa allra talnanna og það dugir því að margfalda hana með fjölda talna n til þess að fá alla summuna.

Sýnidæmi 1

Finnum summu allra náttúrulegra talna frá 1 upp í 100.

Meðaltal fyrsta og síðasta liðs er 101/2 = 50,5. Það margfaldað með fjöldanum 100 gefur 5050.

Bein innsetning í regluna gefur sömu niðurstöðu:

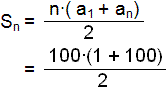
         = 50∙101 = 5050

Sýnidæmi 2

Finnum summu allra tveggja stafa heilla talna.

Fyrsta talan er a₁ = 10 og sú síðasta 99 en okkur vantar að vita númer hvað hún er. Öruggast er að reikna það út.

   a_n = a₁ + (n – 1)∙d

  99 = 10 + (n − 1)∙1

  99 = 9 + n

    n = 99 – 9 = 90

Nú getum við reiknað summuna.

   Meðaltal fyrsta og síðasta liðs er (10 + 99)/2 = 54,5

   Margföldun með fjölda liða gefur  54,5∙90 = 4905

Sýnidæmi 3

Finnum summu raðarinnar  2 + 7 + 12 + 17 + 22 + 27 + 32.

  Þetta er mismunaröð með 7 liði og mismuninn 5.

  Meðaltal fyrsta og síðasta liðs er (2 + 32)/2 = 17.

  Það margfaldað með fjöldanum gefur summuna 17∙7 = 119

Þetta dæmi er sérlega þægilegt að leysa í töflureikninum EXCEL.

1)  Við byrjum á því að rita tvo fyrstu liðina 2 og 7 í reiti A1 og A2.
Síðan blokkum við reitina tvo og færum bendilinn í hægra hornið neðst þar til svartur kross birtist.

2)  Nú höldum við niðri vinstri músarhnappnum og drögum niður í reit A7. Runan birtist þá sjálfkrafa.

3)  Þessu næst setjum við bendilinn í reit A8 og veljum táknið ∑ (lesið sigma) á tækjastikunni. Þá birtist formúlan =SUM(A1:A7) sem býður okkur upp á að leggja saman tölurnar í reitum A1 til A7.

4)  Ef við nú þiggjum það með ENTER-takkanum þá fáum við summuna 119 í reit A8.

Táknið ∑ er oft notað í til þess að tákna summur. Það er þá gert þannig að teljaragildi eru rituð neðan og ofan við táknið.

Neðra gildið (gildið undir tákninu) segir þá til um upphafsnúmer og það efra lokanúmer. Aftan við táknið kemur síðan eitthvað fall af teljaranum n.

T.d. verður eftirfarandi runa svona:

                = 1 + 4 + 9 + 16 + 25 + 36 + 49 = 140

Ef við viljum hins vegar nota summutákn til þess að lýsa röð, t.d.

   2 + 7 + 12 + 17 + 22 + 27 + 32

þá verðum við að finna fall sem gefur liðina út frá númerum þeirra. Til þess notum við regluna a_n = a₁ + (n – 1)∙d. Liðirnir eru 7 og mismuninn d = 5.

   a_n = 2 + (n – 1)∙5 = 2 + 5n – 5 = 5n – 3

Summuna má því rita svona:

                          + (5∙5 – 3) + (5∙6 – 3) + (5∙7 – 3)

                          = 2 + 7 + 12 + 17 + 22 + 27 + 32 = 119

Sýnidæmi 4
Finnum summuna 

Við látum teljarann n hlaupa frá einum upp í 8 og fáum eftirfarandi röð.

   Meðaltalið af fyrsta og síðasta lið er (9 + 16)/2 = 12,5

   Það margföldum við með fjöldanum.

Sýnidæmi 5

Finnum summu allra þriggja stafa talna sem 8 gengur upp í og skrifum röðina með summutákni.

Fyrsta talan er 104 og sú síðasta 992 og mismunurinn d = 8. Út frá þessu getum við reiknað fjöldann.

Við byrjum á því að finna fall af númerinu sem lýsir röðinni.

   a_n = a₁ + (n – 1)∙d

       = 104 + (n – 1)∙8 = 104 + 8n – 8 = 8n + 96

Síðan reiknum við út fjölda liða.

              a_n = a₁ + (n – 1)∙d

           992 = 104 + (n – 1)∙8 = 104 + 8n – 8 = 96 + 8n

   992 – 96 = 8n = 896

               n = 896/8 = 112

Nú getum við sett upp summutákn og reiknað summuna.

                         = 112∙(104 + 992)/2 = 61.376

Sýnidæmi 6

Finnum nú lágmarksfjölda ólíkra þriggja stafa talna sem 8 gengur upp og sem hefur summu yfir 10.000.

   Þetta er væntanlega summan S_n = 992 + 984 + 976 + ∙ ∙ ∙ ∙ ∙ ∙

Við sjáum að d = −8, a₁ = 992 og S_n = 10.000.

Setjum þetta upp í tiltækar reglur.

   S_n = n∙(992 + a_n)/2 = 10.000

   a_n = 992 + (n – 1)∙(−8) = 1000 – 8n.

Setjum a_n úr neðri reglunni inn í þá efri og leysum m.t.t n.

   n∙(992 + 1000 – 8n)/2 = 10.000

      n∙(992 + 1000 – 8n) = 20.000

              n∙(1992 – 8n) = 20.000

Þetta gefur okkur jöfnu af öðru stigi.

   1992n – 8n² = 20.000

Deilum í gegn með –8 og færum til.

   n² – 249n + 2500 = 0    

Leysum þessa jöfnu með formúlunni.

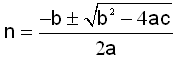
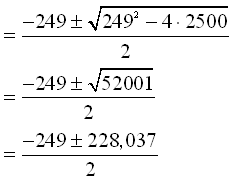
Þetta gefur okkur u.þ.b. lausnirnar 10,5 og 238,5.

Hærri lausnin kemur ekki til greina. Hún verður væntanlega til þegar röðin hefur klárað allar jákvæðar tölur og neikvæðar tölur dragast frá aftur. Þetta er nokkuð löng leið og hér er beðið um lágmarksfjölda. Rétta lausnin er því 10,5 sem segir okkur að þegar ellefti liðurinn bætist við fer summan yfir 10.000 (enda er hver og einn liður rétt undir 1000). Svarið er n = 11.