© 2008 Rasmus ehf og Jóhann Ķsak Pétursson
© 2008 Rasmus ehf og Jóhann Ķsak Pétursson |
Runur og rašir |
|
Žegar kvótarunur eru lagšar saman žį koma fram kvótarašir (eša jafnhlutfallarašir). Viš getum fundiš einfalda reglu til žess aš finna summu žeirra į eftirfarandi hįtt.
Sn = a1 + a1∙k + a1∙k2 + a1∙k3 + ∙ ∙ ∙ ∙ ∙ + a1∙kn−2 + a1∙kn−1
Margföldum nś rununa meš k (hękkum veldiš į k um 1).
Sn∙k = a1∙k + a1∙k2 + a1∙k3 + ∙ ∙ ∙ ∙ ∙ + a1∙kn−1 + a1∙kn
Drögum nś upphaflegu röšina frį.
![]()
Viš sjįum aš flestir liširnir falla śt, jįkvęšir į móti neikvęšum. Žaš sem eftir stendur er eftirfarandi jafna sem viš leysum m.t.t. Sn:
Sn ∙ k Sn = a1 ∙ kn a1
Sn ∙ (k 1) = a1 ∙ (kn 1)
Ef viš nś deilum ķ gegn meš (k 1) žį fįum viš eftirfarandi reglu:
|
|
Finnum summu 10 fyrstu lišanna ķ rununni
1 + 2 + 4 + 8 + 16 + ∙ ∙ ∙ ∙ ∙
Hér er n = 10, k = 2 og a1 = 1. Meira žurfum viš ekki aš vita.
![]()
= 1024 −1 =1023
Flest runudęmi er aušvelt aš leysa ķ töflureikni, en svona setjum viš žetta upp ķ EXCEL.
| 1) | 2) | 3) | 4) |
 |
 |
|
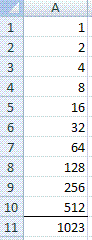 |
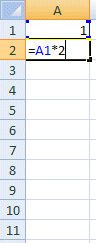
1) Viš byrjum į žvķ aš rita fyrsta lišinn ķ reit A1. Ķ A2 ritum viš svo formśluna =A1*2 sem setur ķ reitinn tvöfalt žaš sem er ķ reitnum fyrir ofan.
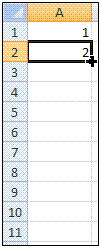
2) Formśluna ķ A2 afritum viš nišur ķ reit A10. Žį birtist röšin tilbśin ķ reitum A1 til A10.
3) Nś leggjum viš saman meš formślunni =SUM(A1:A10) eša meš žvķ aš slį į ∑ į tękjastikunni.
4) Nišurstašan er samhljóša fyrri śtkomu.
Reiknum summu rašarinnar 1 + 3 + 9 + ∙ ∙ ∙ ∙ ∙ ∙177147.
Nś vitum viš ekki fjölda liša žannig aš viš veršum aš byrja į žvķ aš reikna hann śt.
an = a1∙kn−1
177147 = 1∙3n−1
ln 177147 = ln 3n−1
ln 177147 = (n 1) ln 3
ln 177147/ln 3 = n 1
n = 1 + ln 177147/ln 3 = 12
Nś getum viš notaš formśluna.
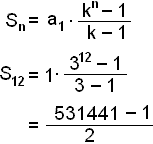
= 265.720
Finnum summu sjö fyrstu liša rašar žar sem a3 = 810.000 og a6 = 590.490.
Viš byrjum į žvķ aš finna k.
Viš sjįum aš k3 hlżtur aš vera hlutfalliš a6/a3.
k3 = 590.490/810.000 = 0,729
![]() =
0,9
=
0,9
Nś žurfum viš aš finna fyrsta lišinn a1. Žaš getum viš t.d. gert meš žvķ aš deila a3 meš k2.
a1 = 810.000/0,92 = 1.000.000
Nś vitum viš žaš sem til žarf til žess aš nota formśluna.
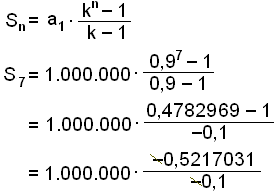
= 5.217.031
Viš sjįum ķ dęminu hér fyrir ofan aš liširnir eru minnkandi eftir žvķ sem n fer hękkandi. Žaš er vegna žess aš kvótinn k er brot į milli -1 og 1 og viš munum aš kvótarunur af žessu tagi kallast samleitnar. Rašir af žessu tagi bera samsvarandi nafn og kallast samleitnar rašir.
|
Kvótarašir eru samleitnar ef −1 < k < 1. |
Viš skulum nś hugsa okkur hlaupara sem er aš leggja af staš ķ 100 m hlaup. Til aš byrja meš hleypur hann helminginn af vegalengdinni eša 50 m. Žessu nęst hleypur hann helminginn af žvķ sem eftir er eša 25 m og sķšan 12,5 m o.s.frv. Žannig mį skipta vegalengdinni sem eftir er nišur ķ óteljandi stöšugt minni og minni helminga. Ef viš höldum óendanlega lengi įfram žį hljótum viš aš komast ķ mark. Meš öšrum oršum žį hafa óendanlegar samleitnar kvótarašir endanlega summu eins og dęmiš hér fyrir nešan sżnir.
100 = 50 + 25 + 12,5 + 6,25 + ∙ ∙ ∙ ∙ ∙ ∙ ∙
Viš skulum nś finna reglu sem gerir okkur kleift aš reikna summur óendanlegra samleitinna kvótraša.
Skošum fyrst hvaš veršur um kn žegar n stefnir į óendanlegt. Ljóst er aš ef k er brot (|k| < 1) žį stefnir kn į 0 og brot sem hafin eru ķ stöšugt hęrra veldi fara lękkandi.
![]()
Viš skulum nś athuga hvernig žetta kemur śt ķ summuformślunni
![]()
Viš notum nś S ķ staš Sn vegna žess aš nś er summan endanleg og n er óendanlegt.
![]()
Ef viš nś margföldum fyrir ofan og nešan meš −1 og lögum jöfnuna til žį veršur hśn eftirfarandi:
|
|
Finnum summu rašarinnar
1 + ½ + ¼ + ⅛ + ∙ ∙ ∙ ∙ ∙ ∙
Viš sjįum aš žetta er samleitin kvótaröš meš k = ½ og notum okkar nżfengnu reglu.
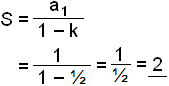
Finnum summu rašarinnar
1 − ½ + ¼ − ⅛ + ∙ ∙ ∙ ∙ ∙ ∙
Ķ röšinni skiptast į + og og liširnir lękka um helming ķ hverju skrefi žannig aš k hlżtur aš vera −½.
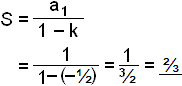
Finnum hvaša gildi k žarf aš taka žannig aš summa óendanlegu rašarinnar 1 + k + k2 + k3 + ∙ ∙ ∙ ∙ ∙ ∙ verši 10.
Ljóst er aš röšin veršur aš vera samleitin og žį gildir eftirfarandi jafna.
![]()
Jöfnuna leysum viš aušveldlega meš žvķ aš margfalda ķ gegn meš (1 k).
1 = 10(1 k) = 10 10k
10k = 10 1 = 9
k = 9/10 = 0,9
Ęfšu žig į žessum ašferšum og taktu sķšan próf
4 ķ Runum og röšum.
ps. mundu eftir aš fylla śt ķ tékklistann žinn jafnóšum