Rasmus ehf Jöfnur II kynning 6 (Su09K06)

Jöfnur II kynning 6

Jöfnur með óþekktu breytuna undir striki

Í jöfnureikningi þar sem brot koma við sögu er einfaldast fyrir okkur að eyða brotunum með því að margfalda alla liði jöfnunnar með heppilegri tölu. Þessi tala er samnefnari brotanna.

Sýnidæmi 1	Leysum jöfnuna
	*Við marg-földum í gegn með 12 þar sem bæði 4 og 6 ganga upp í 12 með deilingu.*
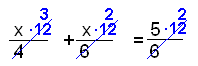	Nefnararnir styttast út
3x + 2x = 10 5x = 10 x = 2	Við einföldum og reiknum út gildið fyrir x

Þegar óþekkta breytan er undir striki þurfum við að hugsa fyrir því að lausnin sem við finnum getur leitt til deilingar með núlli. Við þurfum því að prófa lausnina til þess að ganga úr skugga um að hún gildi. Skoðum eftirfarandi dæmi:

Sýnidæmi 2	Leysum jöfnuna
	*Hér sjáum við að x má ekki vera 0 því þá deilum við með 0.*
	*Við margföldum í gegn með x til þess að eyða brotunum og þá verður eftirleikurinn auðveldur.*
1 = 2 − x x = 2 − 1 = 1	*Þessi lausn er í lagi.*

Sýnidæmi 3	Leysum jöfnuna
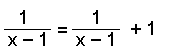	*Hér getur x ekki verið 1 vegna þess að þá deilum við með 0.*
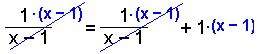	*Við margföldum í gegn með (x − 1) og eyðum brotunum.*
1 = 1 + x − 1 x = 1	*Þessi lausn gengur ekki því þá verða nefnararnir 0 og það er ekki hægt að deila með 0.* *Jafnan hefur enga lausn.*

Sýnidæmi 4	Leysum jöfnuna
	*Í þessari jöfnu getur x ekki tekið gildin 1 og −1.* *Við margföldum í gegn með (x − 1)(x + 1).*

x + 1 − (x − 1) = 2(x² − 1) x + 1 − x + 1 = 2x² − 2	*Margföldum og leysum upp úr svigum*
−2x² = −4 x² = 2 x = ±Ö2	*Leysum upp jöfnuna með tilliti til x* *Þessar lausnir eru í lagi.*

Sýnidæmi 5	Leysum jöfnuna
	*Hér getur x hvorki verið 0 né 2.* *Við marg-földum í gegn með x(x − 2) eða x² − 2x*

x² − 2 = 2x + x − 2 x² − 3x = 0	*Margföldum og leysum upp úr svigum* *og setjum óþekktu stærðirnar öðrum megin*
x(x − 3) = 0 x = 0 eða 3 x = 3	*Með þáttum sjáum við hvaða möguleikar koma til greina.* *0 gildir ekki þannig að x = 3 er eina lausnin.*

Æfðu þig á þessum aðferðum og taktu síðan próf 6. í Jöfnum II.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum.