© 2008  Rasmus ehf    og Jóhann Ísak Pétursson

Heildun

Kynning 7

Heildun með innsetningu

Rifjum upp keðjuregluna, en hana notuðum við til þess að deilda samsett föll. Hún var svona:

   (f(g(x)))´ = f´(g(x))∙g´(x)

Þessa reglu gátum við t.d. notað á eftirfarandi hátt:

Við hljótum að geta notað þessa reglu í hina áttina til þess að heilda. Í það minnsta getum við leyst eftirfarandi heildi:

   = sin x² + C

Þegar við notum keðjuregluna til þess að heilda á þennan hátt þurfum við að hafa til staðar bæði ytra fall v(u) og afleiðu innra fallsins u´. Skoðum dæmi um þetta:

Hér er ytra fallið v(u) = e^u, innra fallið u = sin x og afleiða þess u´ = cos x.

Raunar er ekki alltaf þörf á að finna eitthvað innra og ytra fall til þess að nota þessa aðferð eins og dæmið hér á eftir sýnir.

Hér höfum við heildi af gerð sem rétt er að taka sérstaklega eftir:

Nú er dx ekkert annað en örlítið bil á x-ás sem stefnir á 0 og du samsvarandi breyting á fallgildinu. Afleiðan u´ er því hlutfallið du/dx og við getum unnið með þetta eins og hverja aðra jöfnu.

        du = u´dx

Við sjáum nú að eftirfarandi regla hlýtur að gilda:

Þetta gefur okkur möguleika á að skipta út fallinu u og afleiðu þess u´ fyrir breytuna u.

Þetta getur einfaldað dæmið verulega. Skoðum nú heildið sem við nefndum hér fyrir ofan.

Við sjáum að þetta heildi passar beint inn í regluna. Við köllum sin x = u og þá er cos x = u´ þannig að heildið verður eftirfarandi:

   
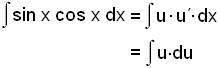
                             = ½∙u² + C

Hér höfum við sett inn breytuna u í staðinn fyrir fallið u og heildað. Nú er aðeins eftir að setja fallið inn aftur í staðinn fyrir u. Niðurstaðan verður eftirfarandi:

Prófum nú þessa niðurstöðu með því að deilda (finnum afleiðu).

   (½∙sin²x + C)´ = ½∙2∙ sin x ∙ cos x + 0 = sin x cos x

Þetta stenst  prófun.

Samkvæmt þessu getum við sett breytuna u inn fyrir fallið u ef við höfum u´dx innan heildisins sem verður þá skipt út fyrir du.

Aðferðin nefnist innsetningaraðferð.

Helstu þættir innsetningaraðferðar eru eftirfarandi:

Sýnidæmi 1

  Finnum eftirfarandi heildi:

Veljum u = ln x. Þá er u´ = 1/x og du = 1/x dx

  Heildum nú með innsetningu.

                  = ½∙u² + C

  Setjum loks fallið u = ln x aftur inn fyrir breytuna u.

  Prófum nú svarið með deildun.

 (½∙(ln x)² + C)´ = ½∙2∙ln x∙1/x + 0 = ln x∙1/x

  Þetta stenst prófun.

Sýnidæmi 2

Reiknum heildið

Hér getum við ekki notað liðun í stofnbrot vegna þess að ekki er hægt að þátta nefnara brotsins. Reynum innsetningu.

Köllum u = x² + 2x + 2

    u´= 2x + 2

    du = (2x + 2) dx = 2(x + 1) dx

    ½ du = (x + 1) dx

  Setjum þetta inn.

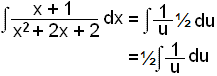
                             = ½∙ln u + C = ½∙ln (x² + 2x + 2) + C

  Prófum nú svarið með deildun.

     (½∙ln (x² + 2x + 2) + C)´ = ½∙(2x + 2)/(x² + 2x + 2) + 0

                                             = (x + 1)/(x² + 2x + 2)
  Þetta stenst.

Sýnidæmi 3

Reiknum heildið

Veljum u = x3 Þá er u´= 3x2 og du = 3x2dx ⅓ du = x2dx

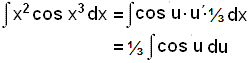                       = ⅓ sin u + C

                       = ⅓ sin x³ + C

Prófun:
(⅓ sin x³ + C)´ = ⅓ cos x³ ∙ 3x² + 0 = x² cos x³

Sýnidæmi 4

Reiknum heildið

Nú eru tveir möguleikar. Köllum fyrst  u =

Þá er

, du =

dx og 2 du =

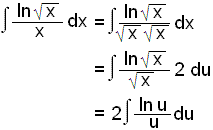
Þetta getum við leyst með hlutheildun eða með því að nota innsetningaraðferðina aftur (sjá sýnidæmi 1).

Veljum nú fallið v = ln u, þá er v´ = 1/u og dv = du/u.

                  = 2∙½∙v² + C = v² + C

   v² + C = (ln u)² + C = (ln)² + C

Þessi tvöfalda innsetning bendir til þess að eitthvað einfaldara hefði mátt reyna.

Skoðum hvað gerist ef við veljum u = ln.

Þá verður u´ =

=

, du =

dx  og  2 du = 1/x dx.

   Heildið okkar verður þá

                                                            = 2∙½∙u² + C

                                                            = (ln)² + C

Við hefðum einnig getað einfaldað heildið með því að skrifa sem x^½ og nota síðan lograregluna ln a^b = b∙ln a. Þá verður heildið svona.

Út úr þessu eigum við að fá  ¼(ln x)² + C (sjá sýnidæmi 1) sem í fljótu bragði virðist ekki það sama og (ln)² + C,
en ekki er allt sem sýnist. Við getum gert eftirfarandi umreikninga:

   ¼(ln x)² + C = ½∙½∙ln x∙ln x + C = ln x^½ ∙ln x^½ + C = (ln)² + C

Niðurstaðan er hin sama.

Þetta dæmi sýnir að margvíslegar innsetningar geta gagnast við lausn heildunardæma og sjálfsagt er að þreifa sig áfram ef svarið liggur ekki ljóst fyrir.

Sýnidæmi 5

Reiknum heildið

Við skulum fyrst skoða innsetninguna u = = (x + 1)^½.

u´ =

, 2 du =

og x + 1 = u2 =

∙

Notum nú þessar innsetningar:

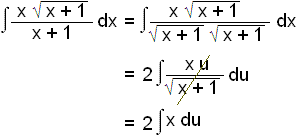
Hér sitjum við uppi með eitt x og verðum að reyna að koma því fyrir sem falli af u. Nú er  u² = x + 1 og þá er x = u² – 1. Setjum það inn fyrir x-ið og heildum.

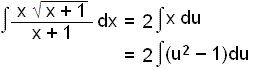
                         = 2(⅓u³ – u) + C

                           = ⅔()³ – 2+ C

Við skulum einnig skoða aðra innsetningu, eða u = x + 1. Þá verður u´= 1 og du = dx.

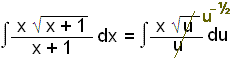
Nú sitjum við aftur uppi með eitt x, en við getum skipt því út fyrir (u – 1) vegna þess að u = x + 1.

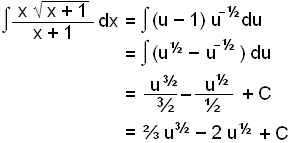
                         =  ⅔()³ – 2+ C