© 2010 Rasmus ehf
© 2010 Rasmus ehf |
Einföldun stæða Kynning 1 |
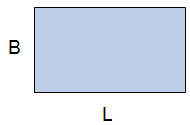 |
Flatarmál ferhyrnings er Breidd (B) • Lengd (L) eða F = B• L Ef lengd L = 4cm og breidd B = 2cm, þá yrði flatarmálið F = 4cm • 2 cm = 8cm² |
Gott er að nota lögmálið um flatarmál ferhyrnings til að útskýra margföldun inní sviga.
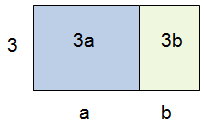 |
Gefum okkur að flötur sé 3 cm á breidd og (a + b) cm á lengd. Þá yrði flatarmálið 3 • (a+b) = 3a + 3b þ.a.e.s samsett úr tveim hlutum sem hafa stærðirnar 3•a og 3•b. |
|
3(a + b) = 3 · a + 3 · b = 3a + 3b |
Við margföldun inní sviga margfaldast sérhver liður inni í sviganum með gildinu sem er utan svigans. |
Ýmis dæmi um margföldun inn í sviga.:
|
7(x + 2) = 7 · x + 7 · 2 = 7x + 14 |
Fyrst er margfaldað uppúr sviga og síðan dregnir saman líkir liðir. |
|
|
3(2 - 3x) = 3 · 2 - 3 · 3x = 6 - 9x |
6x(1 - x) - 4x(2 - 2x) = 6x - 6x2 - 8x + 8x2 = -2x + 2x2
Nánari skýring á þessari mynd.
1. |
6x · 1 = 6x | |
2. |
6x · -x = -6x2 | (+ · - = -) |
3. |
-4x · 2 = -8x | (- · + = -) |
4. |
-4x · -2x = +8x2 | (- · - = +) |
6 + 2(x + 2) = 6 + 2 · x + 2 · 2 = 6 + 2x + 4 = 10 + 2x
Ath. forgangsröð aðgerða fyrst margfalda síðan + og -
Taktu nú próf númer 1 í Einföldun stæða, ef þú færð 80% eða meira skaltu snúa þér að verkefni 2.