Hnitakerfið - jöfnur og gröf 2
| © 2004 Rasmus ehf |
Hnitakerfið - jöfnur og gröf 2 |
|
Kynning 2.
Jöfnur og gröf.
Skurðpunktur tveggja lína. Ef þú hefur tvær jöfnur með tveim óþekktum stærðum þá eru til amk. þrjár leiðir til að rannsaka hvar þær hittast (skerast).
Aðferð 1 teiknuð lausn.
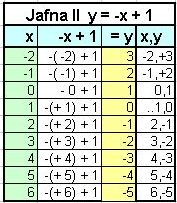
Skoðum jöfnurnar I: y = 2x + 1 og II: y = - x + 1
Fyrst gerum við gildistöflu fyrir hvora jöfnu um sig.
....... 
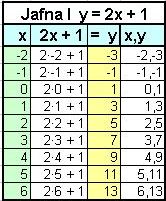Hvenær skildu bæði skilyrðin standast ? Það er þegar einn eða fleiri sameiginlegur punktur finnst þ.a.e.s línurnar skerast. Við teiknum línurnar upp í hnitakerfið.
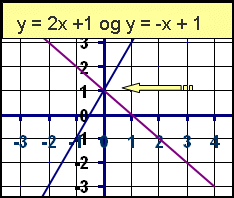
Hér sést að línurnar hittast í punktinum (0,1) Ástæðan fyrir því að þær hittast er sú að þær hafa mismunandi hallatölu. Línur með sömu hallatölu eru alltaf samsíða og hittast því aldrei nema þær falli ofaní hvora aðra, en þá væri um sömu línuna að ræða.
Aðferð 2 samlagningaraðferðin.
Einnig er hægt að finna skurðpunktinn með því að leggja skilyrðin í jöfnunum tveim saman.
I: y = 2x +1
II: y = -x + 1
Við byrjum á því að raða þeim uppá nýtt:
I: -2x + y = + 1
II: x + y = 1
Margföldum jöfnu II: með 2 þá fæst 2(x + y = 1) eða 2x + 2y = 2
Leggjum þær síðan saman:
I: -2x + y = 1
II: 2x + 2y = 2
0 + 3y = 3 þá er y = 1 setjum þá hugmynd inní jöfnu I: þá fæst
að 1 = 2x + 1 flytjum þekktar stærðir til vinstri þá fæst I: +1 -1 = 2x eða 0 = 2x
Þá sést að x = 0.
Þetta kemur heim og saman við teiknuðu lausnina, punkturinn 0,1 er sá eini sem er á báðum þessum ínum.
Aðferð 3 innsetningaraðferðin.
Bæði skilyrðin standast aðeins þegar línurnar hittast, því má fullyrða að y í jöfnu I er sama og y í jöfnu II á því augnabliki.
I: y = 2x +1
II: y = -x + 1
Nú getum við troðið þeirri hugmynd að y = -x + 1 inn í jöfnu I þá fæst að í stað y = 2x +1 fáum við -x + 1 = 2x + 1
Færum þekktar tölur vinstra megin til að allt sé í +.
-1 + 1 = 2x + x eða 0 = 3x þá er x = 0
Setjum þá hugmynd inní í t.d. jöfnu I og þá fæst
y = 2·x +1 = 0 + 1 = 1 Línurnar hittast í punktinum (0,1) eins og áður.
Taktu nú próf 2 úr Jöfnur og gröf sem fjallar um jöfnuhneppi.