Tölfræði
| © 2004 Rasmus ehf |
Tölfræði |
|
Kynning 4
Stöplarit ( stuðlarit), tíðnidreifing, úrtak, vegið meðaltal:
Tíðnidreifing
Skoðum þyngd 30 nemenda í kg. Þessir nemendur eru allir í 10. bekk og er þeim raðað eftir þyngd, þeir léttustu fyrst o.s.frv.
50, 52, 54, 55, 57, 57, 58, 60, 60, 60, 61, 61, 62, 62, 63,
64, 65, 66, 66, 67, 67, 67, 67, 68, 70, 70, 71, 72, 73, 74
Oft er mælingum safnað saman í flokka. Veljum að láta hvern flokk hlaupa á 5 kg.
|
Búum til tíðnitöflu. |
|
| Þyngd í kg. | Tíðni |
| 50 - 54 | 3 |
| 55 - 59 | 4 |
| 60 - 64 | 9 |
| 65 - 69 | 8 |
| 70 - 74 | 6 |
Stöplarit
|
|
|
Sýnum svo tíðnidreifinguna með stöplariti. Stöplaritið birtist fyrir valin talnasvið, þar sem enginn í hópnum sem var mældur reyndist léttari en 50 kg. er þeim hluta skalans sleppt. Slíkt er túlkað með brotinni línu. Stöplarit er með þéttum stöplum sem liggja saman og verða allir að vera jafn breiðir. |
Á myndinni sést að 3 af þessum 30 eru (50 til 54 kg.) eða 10% af hópnum.
Úrtak:
Þegar rannsaka á stórt safn af upplýsingum er oft skynsamlegt að nota Tölfræðina sér til hjálpar. Nú viljum við rannsaka aðgang 10. bekkinga að Internetinu. Það vinnst ekki tími til að spyrja hvern einasta nemenda hvernig aðstæður eru hjá honum. Við tölum við 100 nemendur af handahófi úr grunnskólum á Íslandi. Heildarfjöldi nemenda í 10. bekk er 4500 úrtakið er því 100 nemendur. í úrtakinu eru 50 drengir og 50 stúlkur.
Við spyrjum eftirfarandi spurninga:
Hefur þú aðgang að internetinu heima hjá þér ?
Átt þú eigin einkatölvu sem er tengd við internetið ?
Niðurstöður eru eftirfarandi.
| Spurningar og svör | Tíðni (drengir) | (Tíðni stúlkur) |
Alls |
| Á eigin tölvu | 40 | 35 | 75 |
| Hefur aðgang að netinu | 45 | 40 | 85 |
| Hefur ekki netaðgang | 5 | 10 | 15 |
Nú vorum við svo heppin að hafa úrtakið 100 nemendur þannig að auðvelt er að breyta niðurstöðum í prósentur.
Við sjáum að 85 eða 85% nemenda í úrtakinu hafa aðgang að internetnu þá gætum við spáð fyrir um þann fjölda nemenda í 10. bekk sem hefur netaðgang. Samkvæmt úrtakinu eru það 85% af nemendum. Við reiknum því 85% af 4500 og fáum að 0.85 x 4500 = 3825 . Því getum við fullyrt með nokkurri vissu að rúmlega 3800 nemendur í 10. bekk hafi interntaðgang heima hjá sér.
Svipaðar aðferðir eru notaðar til þess að kanna ýmsa þætti í okkar nánasta umhverfi.
Sem dæmi má nefna:
Fylgi stjórnmálaflokka
Áhorf á sjónvarpsdagskrá
Lestur dagblaða
Stærð fiskistofna
Vegið meðaltal:
Tveir 10.bekkir eru í Séstvallaskóla. Þeir tóku samræmt próf í stærðfræði og var niðurstaðan þessi
10. bekkur A meðaleinkunn 7,0 Fjöldi nemenda var 20
10. bekkur B meðaleinkunn 6,0 Fjöldi nemenda var 30
Við eigum nú að reikna út meðaleinkunn skólans.
Það væri rangt að leggja saman meðaleinkunnir bekkjanna eða 7+ 6= 13 og deila síðan í með 2 og segja meðaltalið er 6,5 því það eru mismargir í hvorum bekk fyrir sig.
Vegið meðaltal.
Við þurfum að finna samanlagða einkunn allra í báðum bekkjunum og deila í þá tölu með samanlögðum fjölda einstaklinga í báðum bekkjunum.
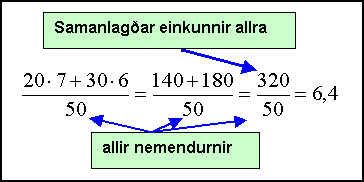
Við reiknum út vegið meðaltal með því að finna summu allra einkunna og deila í með fjölda einstaklinga. Vegið meðaltal er 6,4 en ekki 6,5
Æfðu þig á þessum aðferðum og taktu síðan próf 4 í Tölfræði.
ps. mundu eftir að fylla út í tékklistann þinn jafnóðum.
